Question Number 33450 by ajfour last updated on 16/Apr/18

Commented by ajfour last updated on 16/Apr/18

$${Find}\:{electric}\:{flux}\:{of}\:{a}\:{semiinfinite} \\ $$$${thread}\:{of}\:{charge}\:{having}\:{linear} \\ $$$${charge}\:{density}\:\lambda,\:{through}\:{a}\:{circular} \\ $$$${disc}\:{of}\:{radius}\:{R}\:{if}\:{one}\:{end}\:{of}\:{the} \\ $$$${thread}\:{is}\:{at}\:{the}\:{centre}\:{of}\:{this} \\ $$$${circular}\:{area}. \\ $$
Answered by 33 last updated on 18/Apr/18
![consider an element of lenght dx at dist x from centre of ring dφ = (dq/(2ε_0 ))(1−(x/( (√(R^2 +x^2 ))))) φ = ∫_( 0) ^( L) (((λdx))/(2ε_0 )) (1−(x/( (√(R^2 + x^2 ))))) ⇒ φ = (λ/(2ε_0 ))[x− (√(x^2 + R^2 )) ]_0 ^L φ = (λ/(2ε_0 ))lim_(L→∞) {L−(√(L^2 +R^2 )) +R} φ = ((λR)/(2ε_0 ))](https://www.tinkutara.com/question/Q33475.png)
$${consider}\:{an}\:{element} \\ $$$${of}\:{lenght}\:{dx}\:{at}\:{dist}\:{x}\: \\ $$$${from}\:{centre}\:{of}\:\:{ring} \\ $$$$ \\ $$$${d}\phi\:=\:\:\frac{{dq}}{\mathrm{2}\epsilon_{\mathrm{0}} }\left(\mathrm{1}−\frac{{x}}{\:\sqrt{{R}^{\mathrm{2}} +{x}^{\mathrm{2}} }}\right) \\ $$$$\phi\:=\:\underset{\:\:\mathrm{0}} {\overset{\:\:\:\:{L}} {\int}}\:\:\frac{\left(\lambda{dx}\right)}{\mathrm{2}\epsilon_{\mathrm{0}} }\:\left(\mathrm{1}−\frac{{x}}{\:\sqrt{{R}^{\mathrm{2}} \:+\:{x}^{\mathrm{2}} }}\right) \\ $$$$\Rightarrow\:\phi\:=\:\frac{\lambda}{\mathrm{2}\epsilon_{\mathrm{0}} \:}\left[{x}−\:\sqrt{{x}^{\mathrm{2}} \:+\:{R}^{\mathrm{2}} }\:\right]_{\mathrm{0}} ^{{L}} \\ $$$$\phi\:=\:\:\frac{\lambda}{\mathrm{2}\epsilon_{\mathrm{0}} }{li}\underset{{L}\rightarrow\infty} {{m}}\left\{{L}−\sqrt{{L}^{\mathrm{2}} +{R}^{\mathrm{2}} }\:+{R}\right\} \\ $$$$\phi\:=\:\frac{\lambda{R}}{\mathrm{2}\epsilon_{\mathrm{0}} } \\ $$
Commented by ajfour last updated on 17/Apr/18
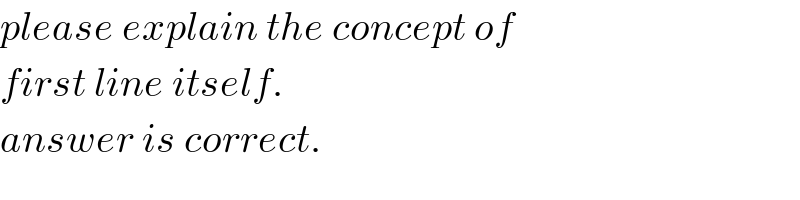
$${please}\:{explain}\:{the}\:{concept}\:{of} \\ $$$${first}\:{line}\:{itself}. \\ $$$${answer}\:{is}\:{correct}. \\ $$
Commented by 33 last updated on 19/Apr/18
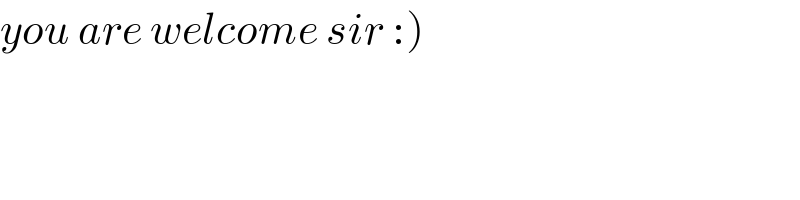
$$\left.{you}\:{are}\:{welcome}\:{sir}\::\right) \\ $$
Commented by 33 last updated on 18/Apr/18

$${for}\:{a}\:{point}\:{charge}\:{placed} \\ $$$${at}\:{the}\:{axis}\:{of}\:{ring}\:\:{at}\:{dist}\:'{x}' \\ $$$${flux}\:{through}\:{the}\:{disk}\:{can}\:{be} \\ $$$${calculated} \\ $$$$\: \\ $$$${we}\:{can}\:{make}\:{an}\:{imaginary} \\ $$$${curved}\:{surface}\:\left({a}\:{part}\:{of}\:{sphere}\right){with}\:{boundary} \\ $$$${as}\:{the}\:{ring}\:{and}\:{its} \\ $$$${centre}\:{coinciding}\:{with}\:{the}\: \\ $$$${position}\:{of}\:{point}\:{charge}.\: \\ $$$$ \\ $$$$\:\phi\:=\:\left(\:{total}\:{flux}\right)\:\frac{{area}\:{of}\:{surface}}{{area}\:{of}\:{sphere}} \\ $$
Commented by 33 last updated on 18/Apr/18

Commented by 33 last updated on 18/Apr/18

$${x}\:\neq\:\mathrm{0} \\ $$
Commented by 33 last updated on 18/Apr/18

$${is}\:{that}\:{ok}\:{sir}? \\ $$
Commented by ajfour last updated on 18/Apr/18
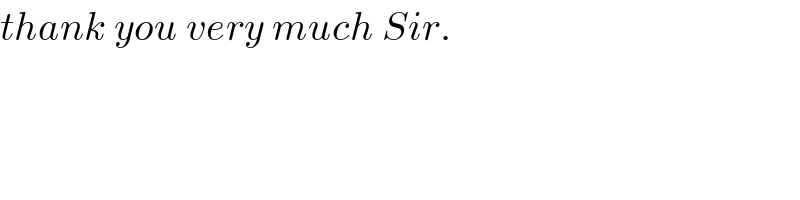
$${thank}\:{you}\:{very}\:{much}\:{Sir}. \\ $$
