Question Number 34231 by byaw last updated on 03/May/18

Answered by MJS last updated on 03/May/18
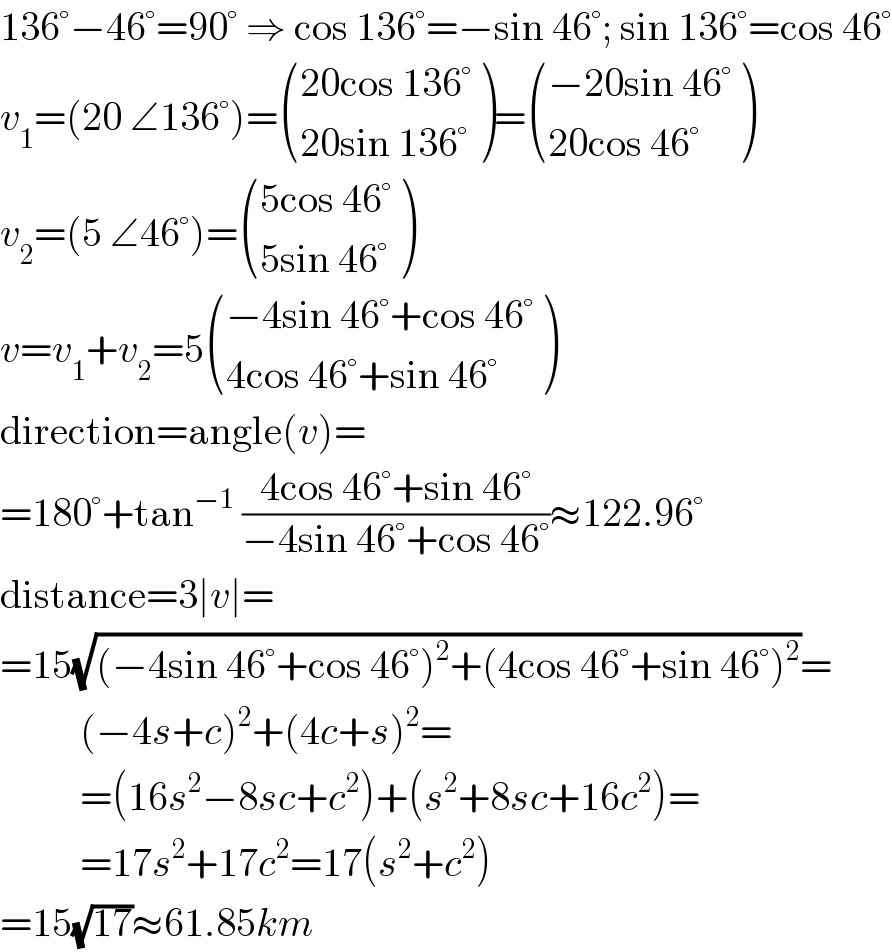
$$\mathrm{136}°−\mathrm{46}°=\mathrm{90}°\:\Rightarrow\:\mathrm{cos}\:\mathrm{136}°=−\mathrm{sin}\:\mathrm{46}°;\:\mathrm{sin}\:\mathrm{136}°=\mathrm{cos}\:\mathrm{46}° \\ $$$${v}_{\mathrm{1}} =\left(\mathrm{20}\:\angle\mathrm{136}°\right)=\begin{pmatrix}{\mathrm{20cos}\:\mathrm{136}°}\\{\mathrm{20sin}\:\mathrm{136}°}\end{pmatrix}=\begin{pmatrix}{−\mathrm{20sin}\:\mathrm{46}°}\\{\mathrm{20cos}\:\mathrm{46}°}\end{pmatrix} \\ $$$${v}_{\mathrm{2}} =\left(\mathrm{5}\:\angle\mathrm{46}°\right)=\begin{pmatrix}{\mathrm{5cos}\:\mathrm{46}°}\\{\mathrm{5sin}\:\mathrm{46}°}\end{pmatrix} \\ $$$${v}={v}_{\mathrm{1}} +{v}_{\mathrm{2}} =\mathrm{5}\begin{pmatrix}{−\mathrm{4sin}\:\mathrm{46}°+\mathrm{cos}\:\mathrm{46}°}\\{\mathrm{4cos}\:\mathrm{46}°+\mathrm{sin}\:\mathrm{46}°}\end{pmatrix} \\ $$$$\mathrm{direction}=\mathrm{angle}\left({v}\right)= \\ $$$$=\mathrm{180}°+\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{4cos}\:\mathrm{46}°+\mathrm{sin}\:\mathrm{46}°}{−\mathrm{4sin}\:\mathrm{46}°+\mathrm{cos}\:\mathrm{46}°}\approx\mathrm{122}.\mathrm{96}° \\ $$$$\mathrm{distance}=\mathrm{3}\mid{v}\mid= \\ $$$$=\mathrm{15}\sqrt{\left(−\mathrm{4sin}\:\mathrm{46}°+\mathrm{cos}\:\mathrm{46}°\right)^{\mathrm{2}} +\left(\mathrm{4cos}\:\mathrm{46}°+\mathrm{sin}\:\mathrm{46}°\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(−\mathrm{4}{s}+{c}\right)^{\mathrm{2}} +\left(\mathrm{4}{c}+{s}\right)^{\mathrm{2}} = \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{16}{s}^{\mathrm{2}} −\mathrm{8}{sc}+{c}^{\mathrm{2}} \right)+\left({s}^{\mathrm{2}} +\mathrm{8}{sc}+\mathrm{16}{c}^{\mathrm{2}} \right)= \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{17}{s}^{\mathrm{2}} +\mathrm{17}{c}^{\mathrm{2}} =\mathrm{17}\left({s}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$=\mathrm{15}\sqrt{\mathrm{17}}\approx\mathrm{61}.\mathrm{85}{km} \\ $$
