Menu Close

Question-34355

Tinku Tara 0 Comments
Pin




Question Number 34355 by srikarkailash9@gmail.com last updated on 05/May/18
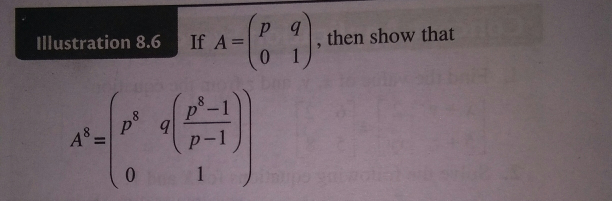
Commented by math khazana by abdo last updated on 05/May/18
let prove by recurrence that A^n = (((p^n q((p^n −1)/(p−1)))),((0 1)) ) with p≠1 for n=1 A^1 = (((p q)),((0 1)) ) relation true let suppose A^n = (((p^n q((p^n −1)/(p−1)))),((0 1)) ) A^(n+1) = A^n .A= (((p^n q((p^n −1)/(p−1)))),((0 1)) ) . (((p q )),((0 1)) ) = (((p^(n+1) p^n q +q((p^n −1)/(p−1)))),((0 1)) ) = (((p^(n+1) q( ((p^(n+1) −p^n +p^n −1)/(p−1))))),((0 1)) ) = (((p^(n+1) q((p^(n+1) −1)/(p−1)))),((0 1)) ) the relation is true at term n+1 let take n=8 ⇒ A^8 = (((p^8 q((p^8 −1)/(p−1)))),((0 1)) )
$${let}\:{prove}\:{by}\:{recurrence}\:{that}\: \\ $$$${A}^{{n}} \:=\:\begin{pmatrix}{{p}^{{n}} \:\:\:\:\:\:\:\:{q}\frac{{p}^{{n}} −\mathrm{1}}{{p}−\mathrm{1}}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${with}\:{p}\neq\mathrm{1}\:{for}\:{n}=\mathrm{1}\:\:{A}^{\mathrm{1}} =\:\begin{pmatrix}{{p}\:\:\:\:\:\:\:\:{q}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${relation}\:{true}\:{let}\:{suppose}\:{A}^{{n}} \:=\:\begin{pmatrix}{{p}^{{n}} \:\:\:\:\:\:\:\:\:{q}\frac{{p}^{{n}} −\mathrm{1}}{{p}−\mathrm{1}}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${A}^{{n}+\mathrm{1}} \:=\:{A}^{{n}} .{A}=\:\begin{pmatrix}{{p}^{{n}} \:\:\:\:\:\:\:{q}\frac{{p}^{{n}} −\mathrm{1}}{{p}−\mathrm{1}}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:\:\:.\begin{pmatrix}{{p}\:\:\:\:\:\:\:\:{q}\:\:}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$=\:\:\:\begin{pmatrix}{{p}^{{n}+\mathrm{1}} \:\:\:\:\:\:\:\:{p}^{{n}} {q}\:+{q}\frac{{p}^{{n}} −\mathrm{1}}{{p}−\mathrm{1}}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$=\:\begin{pmatrix}{{p}^{{n}+\mathrm{1}} \:\:\:\:\:\:\:\:\:\:{q}\left(\:\:\frac{{p}^{{n}+\mathrm{1}} \:−{p}^{{n}} \:+{p}^{{n}} −\mathrm{1}}{{p}−\mathrm{1}}\right)}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$=\:\begin{pmatrix}{{p}^{{n}+\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\:{q}\frac{{p}^{{n}+\mathrm{1}} \:−\mathrm{1}}{{p}−\mathrm{1}}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${the}\:{relation}\:{is}\:{true}\:{at}\:{term}\:{n}+\mathrm{1}\:{let}\:{take}\:\:{n}=\mathrm{8}\:\Rightarrow \\ $$$${A}^{\mathrm{8}} \:\:=\:\begin{pmatrix}{{p}^{\mathrm{8}} \:\:\:\:\:\:\:\:{q}\frac{{p}^{\mathrm{8}} −\mathrm{1}}{{p}−\mathrm{1}}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$
Answered by srikarkailash9@gmail.com last updated on 05/May/18
solve it step wise
$${solve}\:{it}\:{step}\:{wise} \\ $$
Answered by candre last updated on 05/May/18
A^1 = ((p,q),(0,1) ) A^n = ((a_n ,b_n ),(c_n ,d_n ) ) A^(n+1) = ((a_(n+1) ,b_(n+1) ),(c_(n+1) ,d_(n+1) ) ) =A^n A = ((a_n ,b_n ),(c_n ,d_n ) ) ((p,q),(0,1) ) = (((a_n p),(a_n q+b_n )),((c_n p),(c_n q+d_n )) ) from where we get { ((a_(n+1) =a_n p),(a_1 =p)),((b_(n+1) =a_n q+b_n ),(b_1 =q)),((c_(n+1) =c_n p),(c_1 =0)),((d_(n+1) =c_n q+d_n ),(d_1 =0)) :} studing each separated for a a_2 =a_1 p a_3 =a_2 p=a_1 p^2 ⋮ a_n =a_1 p^(n−1) ⇒a_(n+1) =a_n p=a_1 p^n a_1 =p⇒a_n =pp^(n−1) =p^n for c similiar argument apply, but: c_1 =0⇒c_n =c_1 p^(n−1) =0 for b b_2 =a_1 q+b_1 b_3 =a_2 q+b_2 =(a_1 +a_2 )q+b_1 ⋮ b_n =(a_1 +...+a_(n−1) )q+b_1 ⇒b_(n+1) =a_n q+b_n =(a_1 +...+a_(n−1) +a_n )q+b_1 a_n =p^n ⇒Σ_(i=1) ^n a_i =p+p^2 +...+p^n =p((p^n −1)/(p−1))=((p^(n+1) −p)/(p−1))(p≠1) b_1 =q⇒b_n =qΣ_(i=1) ^(n−1) a_i +q=q(((p^n −p)/(p−1))+1)=q((p^n −p+p−1)/(p−1))=q((p^n −1)/(p−1)) similiar for d c_n =0⇒Σ_(i=1) ^n c_i =0 d_1 =1⇒d_n =qΣ_(i=1) ^(n−1) c_n +d_1 =1 so A^n = ((p^n ,(q((p^n −1)/(p−1)))),(0,1) ) where p≠1 above is just the case of n=8
$${A}^{\mathrm{1}} =\begin{pmatrix}{{p}}&{{q}}\\{\mathrm{0}}&{\mathrm{1}}\end{pmatrix} \\ $$$${A}^{{n}} =\begin{pmatrix}{{a}_{{n}} }&{{b}_{{n}} }\\{{c}_{{n}} }&{{d}_{{n}} }\end{pmatrix} \\ $$$${A}^{{n}+\mathrm{1}} =\begin{pmatrix}{{a}_{{n}+\mathrm{1}} }&{{b}_{{n}+\mathrm{1}} }\\{{c}_{{n}+\mathrm{1}} }&{{d}_{{n}+\mathrm{1}} }\end{pmatrix} \\ $$$$={A}^{{n}} {A} \\ $$$$=\begin{pmatrix}{{a}_{{n}} }&{{b}_{{n}} }\\{{c}_{{n}} }&{{d}_{{n}} }\end{pmatrix}\begin{pmatrix}{{p}}&{{q}}\\{\mathrm{0}}&{\mathrm{1}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{{a}_{{n}} {p}}&{{a}_{{n}} {q}+{b}_{{n}} }\\{{c}_{{n}} {p}}&{{c}_{{n}} {q}+{d}_{{n}} }\end{pmatrix} \\ $$$$\mathrm{from}\:\mathrm{where}\:\mathrm{we}\:\mathrm{get} \\ $$$$\begin{cases}{{a}_{{n}+\mathrm{1}} ={a}_{{n}} {p}}&{{a}_{\mathrm{1}} ={p}}\\{{b}_{{n}+\mathrm{1}} ={a}_{{n}} {q}+{b}_{{n}} }&{{b}_{\mathrm{1}} ={q}}\\{{c}_{{n}+\mathrm{1}} ={c}_{{n}} {p}}&{{c}_{\mathrm{1}} =\mathrm{0}}\\{{d}_{{n}+\mathrm{1}} ={c}_{{n}} {q}+{d}_{{n}} }&{{d}_{\mathrm{1}} =\mathrm{0}}\end{cases} \\ $$$$\mathrm{studing}\:\mathrm{each}\:\mathrm{separated} \\ $$$$\mathrm{for}\:\mathrm{a} \\ $$$${a}_{\mathrm{2}} ={a}_{\mathrm{1}} {p} \\ $$$${a}_{\mathrm{3}} ={a}_{\mathrm{2}} {p}={a}_{\mathrm{1}} {p}^{\mathrm{2}} \\ $$$$\vdots \\ $$$${a}_{{n}} ={a}_{\mathrm{1}} {p}^{{n}−\mathrm{1}} \Rightarrow{a}_{{n}+\mathrm{1}} ={a}_{{n}} {p}={a}_{\mathrm{1}} {p}^{{n}} \\ $$$${a}_{\mathrm{1}} ={p}\Rightarrow{a}_{{n}} ={pp}^{{n}−\mathrm{1}} ={p}^{{n}} \\ $$$$\mathrm{for}\:\mathrm{c}\:\mathrm{similiar}\:\mathrm{argument}\:\mathrm{apply},\:{but}: \\ $$$${c}_{\mathrm{1}} =\mathrm{0}\Rightarrow{c}_{{n}} ={c}_{\mathrm{1}} {p}^{{n}−\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{for}\:\mathrm{b} \\ $$$${b}_{\mathrm{2}} ={a}_{\mathrm{1}} {q}+{b}_{\mathrm{1}} \\ $$$${b}_{\mathrm{3}} ={a}_{\mathrm{2}} {q}+{b}_{\mathrm{2}} =\left({a}_{\mathrm{1}} +{a}_{\mathrm{2}} \right){q}+{b}_{\mathrm{1}} \\ $$$$\vdots \\ $$$${b}_{{n}} =\left({a}_{\mathrm{1}} +…+{a}_{{n}−\mathrm{1}} \right){q}+{b}_{\mathrm{1}} \Rightarrow{b}_{{n}+\mathrm{1}} ={a}_{{n}} {q}+{b}_{{n}} =\left({a}_{\mathrm{1}} +…+{a}_{{n}−\mathrm{1}} +{a}_{{n}} \right){q}+{b}_{\mathrm{1}} \\ $$$${a}_{{n}} ={p}^{{n}} \Rightarrow\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} ={p}+{p}^{\mathrm{2}} +…+{p}^{{n}} ={p}\frac{{p}^{{n}} −\mathrm{1}}{{p}−\mathrm{1}}=\frac{{p}^{{n}+\mathrm{1}} −{p}}{{p}−\mathrm{1}}\left({p}\neq\mathrm{1}\right) \\ $$$${b}_{\mathrm{1}} ={q}\Rightarrow{b}_{{n}} ={q}\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{i}} +{q}={q}\left(\frac{{p}^{{n}} −{p}}{{p}−\mathrm{1}}+\mathrm{1}\right)={q}\frac{{p}^{{n}} −{p}+{p}−\mathrm{1}}{{p}−\mathrm{1}}={q}\frac{{p}^{{n}} −\mathrm{1}}{{p}−\mathrm{1}} \\ $$$$\mathrm{similiar}\:\mathrm{for}\:\mathrm{d} \\ $$$${c}_{{n}} =\mathrm{0}\Rightarrow\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{c}_{{i}} =\mathrm{0} \\ $$$${d}_{\mathrm{1}} =\mathrm{1}\Rightarrow{d}_{{n}} ={q}\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{c}_{{n}} +{d}_{\mathrm{1}} =\mathrm{1} \\ $$$${so} \\ $$$${A}^{{n}} =\begin{pmatrix}{{p}^{{n}} }&{{q}\frac{{p}^{{n}} −\mathrm{1}}{{p}−\mathrm{1}}}\\{\mathrm{0}}&{\mathrm{1}}\end{pmatrix}\:\:\:\:\:\mathrm{where}\:{p}\neq\mathrm{1} \\ $$$$\mathrm{above}\:\mathrm{is}\:\mathrm{just}\:\mathrm{the}\:\mathrm{case}\:\mathrm{of}\:{n}=\mathrm{8} \\ $$
Commented by candre last updated on 05/May/18
if p=1 we get A^n = ((1,(qn)),(0,1) ) ;)
$$\mathrm{if}\:{p}=\mathrm{1}\:\mathrm{we}\:\mathrm{get} \\ $$$${A}^{{n}} =\begin{pmatrix}{\mathrm{1}}&{{qn}}\\{\mathrm{0}}&{\mathrm{1}}\end{pmatrix} \\ $$$$\left.;\right) \\ $$
Commented by abdo mathsup 649 cc last updated on 05/May/18
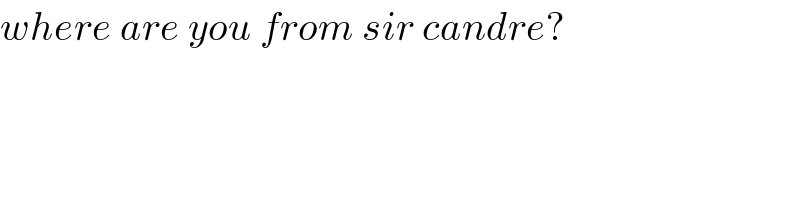
where are you from sir candre?
$${where}\:{are}\:{you}\:{from}\:{sir}\:{candre}? \\ $$
Commented by candre last updated on 05/May/18
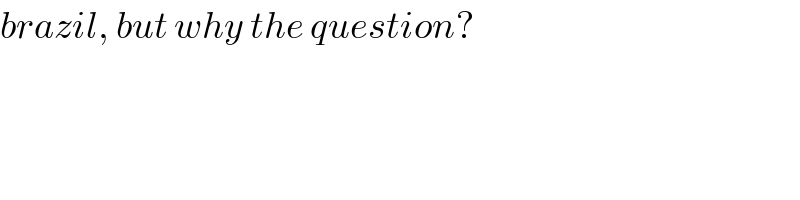
brazil, but why the question?
$${brazil},\:{but}\:{why}\:{the}\:{question}? \\ $$
Commented by math khazana by abdo last updated on 05/May/18
its only a simlple information sir i know that brazil is a beautiful country with good and generous people i am looking that you are most interested to mathematics...i hope to visit brazil some day....
$${its}\:{only}\:{a}\:{simlple}\:{information}\:{sir}\:{i}\:{know}\:{that}\: \\ $$$${brazil}\:{is}\:{a}\:{beautiful}\:{country}\:{with}\:{good}\:{and} \\ $$$${generous}\:{people}\:{i}\:{am}\:{looking}\:{that}\:{you}\:{are}\:{most} \\ $$$${interested}\:{to}\:{mathematics}…{i}\:{hope}\:{to}\:{visit}\:{brazil} \\ $$$${some}\:{day}…. \\ $$
Commented by Rio Mike last updated on 06/May/18
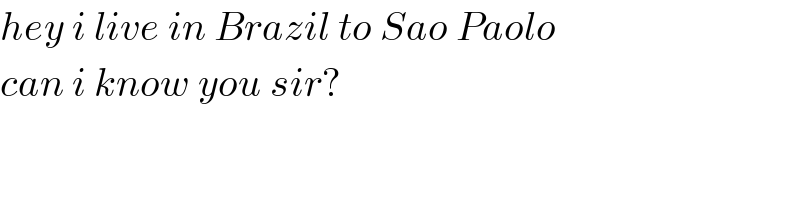
hey i live in Brazil to Sao Paolo can i know you sir?
$${hey}\:{i}\:{live}\:{in}\:{Brazil}\:{to}\:{Sao}\:{Paolo}\: \\ $$$${can}\:{i}\:{know}\:{you}\:{sir}? \\ $$
Commented by candre last updated on 11/May/18
i does live in state of sao paulo, but not the city.
$$\mathrm{i}\:\mathrm{does}\:\mathrm{live}\:\mathrm{in}\:\mathrm{state}\:\mathrm{of}\:\mathrm{sao}\:\mathrm{paulo},\:\mathrm{but}\:\mathrm{not}\:\mathrm{the}\:\mathrm{city}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *