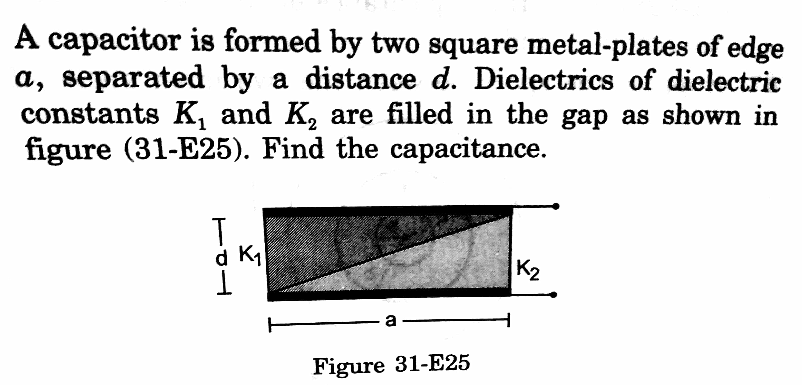
Question Number 34501 by rahul 19 last updated on 07/May/18
Commented by rahul 19 last updated on 07/May/18
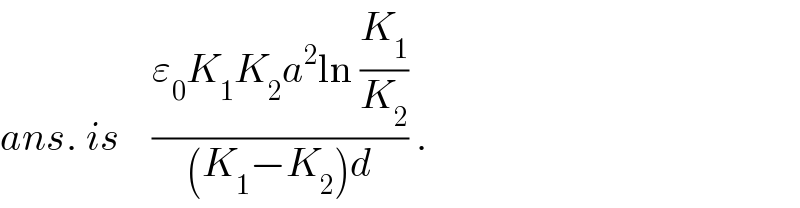
$${ans}.\:{is}\:\:\:\:\frac{\varepsilon_{\mathrm{0}} {K}_{\mathrm{1}} {K}_{\mathrm{2}} {a}^{\mathrm{2}} \mathrm{ln}\:\frac{{K}_{\mathrm{1}} }{{K}_{\mathrm{2}} }}{\left({K}_{\mathrm{1}} −{K}_{\mathrm{2}} \right){d}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/May/18
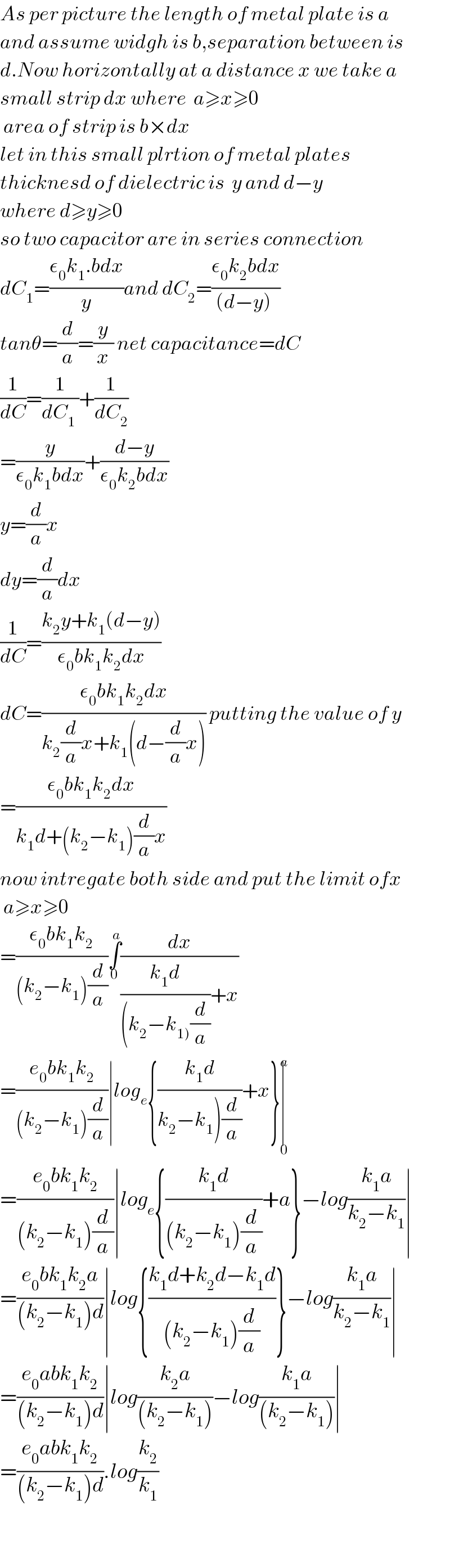
$${As}\:{per}\:{picture}\:{the}\:{length}\:{of}\:{metal}\:{plate}\:{is}\:{a}\: \\ $$$${and}\:{assume}\:{widgh}\:{is}\:{b},{separation}\:{between}\:{is} \\ $$$${d}.{Now}\:{horizontally}\:{at}\:{a}\:{distance}\:{x}\:{we}\:{take}\:{a}\: \\ $$$${small}\:{strip}\:{dx}\:{where}\:\:{a}\geqslant{x}\geqslant\mathrm{0} \\ $$$$\:{area}\:{of}\:{strip}\:{is}\:{b}×{dx} \\ $$$${let}\:{in}\:{this}\:{small}\:{plrtion}\:{of}\:{metal}\:{plates}\: \\ $$$${thicknesd}\:{of}\:{dielectric}\:{is}\:\:{y}\:{and}\:{d}−{y} \\ $$$${where}\:{d}\geqslant{y}\geqslant\mathrm{0} \\ $$$${so}\:{two}\:{capacitor}\:{are}\:{in}\:{series}\:{connection} \\ $$$${dC}_{\mathrm{1}} =\frac{\epsilon_{\mathrm{0}} {k}_{\mathrm{1}} .{bdx}}{{y}}{and}\:{dC}_{\mathrm{2}} =\frac{\epsilon_{\mathrm{0}} {k}_{\mathrm{2}} {bdx}}{\left({d}−{y}\right)\:} \\ $$$${tan}\theta=\frac{{d}}{{a}}=\frac{{y}}{{x}}\:{net}\:{capacitance}={dC} \\ $$$$\frac{\mathrm{1}}{{dC}}=\frac{\mathrm{1}}{{dC}_{\mathrm{1}} \:}+\frac{\mathrm{1}}{{dC}_{\mathrm{2}} } \\ $$$$=\frac{{y}}{\epsilon_{\mathrm{0}} {k}_{\mathrm{1}} {bdx}}+\frac{{d}−{y}}{\epsilon_{\mathrm{0}} {k}_{\mathrm{2}} {bdx}} \\ $$$${y}=\frac{{d}}{{a}}{x} \\ $$$${dy}=\frac{{d}}{{a}}{dx} \\ $$$$\frac{\mathrm{1}}{{dC}}=\frac{{k}_{\mathrm{2}} {y}+{k}_{\mathrm{1}} \left({d}−{y}\right)}{\epsilon_{\mathrm{0}} {bk}_{\mathrm{1}} {k}_{\mathrm{2}} {dx}} \\ $$$${dC}=\frac{\epsilon_{\mathrm{0}} {bk}_{\mathrm{1}} {k}_{\mathrm{2}} {dx}}{{k}_{\mathrm{2}} \frac{{d}}{{a}}{x}+{k}_{\mathrm{1}} \left({d}−\frac{{d}}{{a}}{x}\right)}\:{putting}\:{the}\:{value}\:{of}\:{y} \\ $$$$=\frac{\epsilon_{\mathrm{0}} {bk}_{\mathrm{1}} {k}_{\mathrm{2}} {dx}}{{k}_{\mathrm{1}} {d}+\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right)\frac{{d}}{{a}}{x}} \\ $$$${now}\:{intregate}\:{both}\:{side}\:{and}\:{put}\:{the}\:{limit}\:{ofx} \\ $$$$\:{a}\geqslant{x}\geqslant\mathrm{0} \\ $$$$=\frac{\epsilon_{\mathrm{0}} {bk}_{\mathrm{1}} {k}_{\mathrm{2}} }{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right)\frac{{d}}{{a}}}\underset{\mathrm{0}} {\overset{{a}} {\int}}\frac{{dx}}{\frac{{k}_{\mathrm{1}} {d}}{\left({k}_{\mathrm{2}} −{k}_{\left.\mathrm{1}\right)} \frac{{d}}{{a}}\right.}+{x}} \\ $$$$=\frac{{e}_{\mathrm{0}} {bk}_{\mathrm{1}} {k}_{\mathrm{2}} }{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right)\frac{{d}}{{a}}}\mid{log}_{{e}} \left\{\frac{{k}_{\mathrm{1}} {d}}{\left.{k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right)\frac{{d}}{{a}}}+{x}\right\}\underset{\mathrm{0}} {\overset{{a}} {\mid}} \\ $$$$=\frac{{e}_{\mathrm{0}} {bk}_{\mathrm{1}} {k}_{\mathrm{2}} }{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right)\frac{{d}}{{a}}}\mid{log}_{{e}} \left\{\frac{{k}_{\mathrm{1}} {d}}{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right)\frac{{d}}{{a}}}+{a}\right\}−{log}\frac{{k}_{\mathrm{1}} {a}}{{k}_{\mathrm{2}} −{k}_{\mathrm{1}} }\mid \\ $$$$=\frac{{e}_{\mathrm{0}} {bk}_{\mathrm{1}} {k}_{\mathrm{2}} {a}}{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right){d}}\mid{log}\left\{\frac{{k}_{\mathrm{1}} {d}+{k}_{\mathrm{2}} {d}−{k}_{\mathrm{1}} {d}}{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right)\frac{{d}}{{a}}}\right\}−{log}\frac{{k}_{\mathrm{1}} {a}}{{k}_{\mathrm{2}} −{k}_{\mathrm{1}} }\mid \\ $$$$=\frac{{e}_{\mathrm{0}} {abk}_{\mathrm{1}} {k}_{\mathrm{2}} }{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right){d}}\mid{log}\frac{{k}_{\mathrm{2}} {a}}{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right)}−{log}\frac{{k}_{\mathrm{1}} {a}}{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right)}\mid \\ $$$$=\frac{{e}_{\mathrm{0}} {abk}_{\mathrm{1}} {k}_{\mathrm{2}} }{\left({k}_{\mathrm{2}} −{k}_{\mathrm{1}} \right){d}}.{log}\frac{{k}_{\mathrm{2}} }{{k}_{\mathrm{1}} } \\ $$$$ \\ $$
Commented by rahul 19 last updated on 07/May/18

$${Thank}\:{you}\:{sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 08/May/18
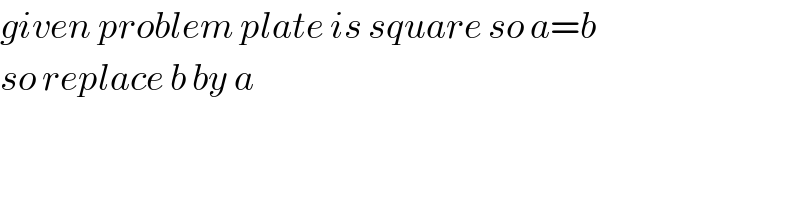
$${given}\:{problem}\:{plate}\:{is}\:{square}\:{so}\:{a}={b}\:\: \\ $$$${so}\:{replace}\:{b}\:{by}\:{a} \\ $$
