Question-34585

Question Number 34585 by tawa tawa last updated on 08/May/18

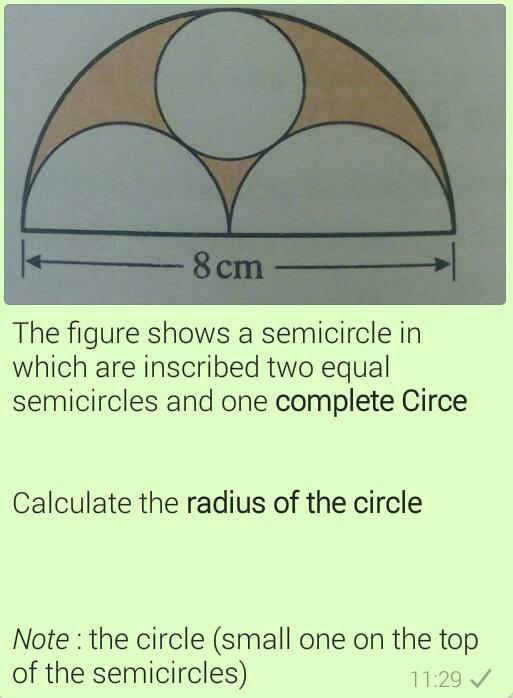
Commented by Rasheed.Sindhi last updated on 08/May/18

Not related to above.... Q#34429 by S@ty@m: 3^m +3^n +1 is not a perfect square. I′ve tried to provide a proof. Anyone who is interested in the question can see my proof.Critical comments will be welcomed.

$$\mathcal{N}{ot}\:{related}\:{to}\:{above}…. \\ $$$$\mathrm{Q}#\mathrm{34429}\:\mathrm{by}\:\mathrm{S}@\mathrm{ty}@\mathrm{m}:\:\mathrm{3}^{\mathrm{m}} +\mathrm{3}^{\mathrm{n}} +\mathrm{1}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}.\:\mathrm{I}'\mathrm{ve}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{provide} \\ $$$$\mathrm{a}\:\mathrm{proof}.\:\mathrm{Anyone}\:\mathrm{who}\:\mathrm{is}\:\mathrm{interested}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{question}\:\mathrm{can}\:\mathrm{see}\:\mathrm{my}\:\mathrm{proof}.\mathrm{Critical} \\ $$$$\mathrm{comments}\:\mathrm{will}\:\mathrm{be}\:\mathrm{welcomed}. \\ $$

Answered by MJS last updated on 09/May/18

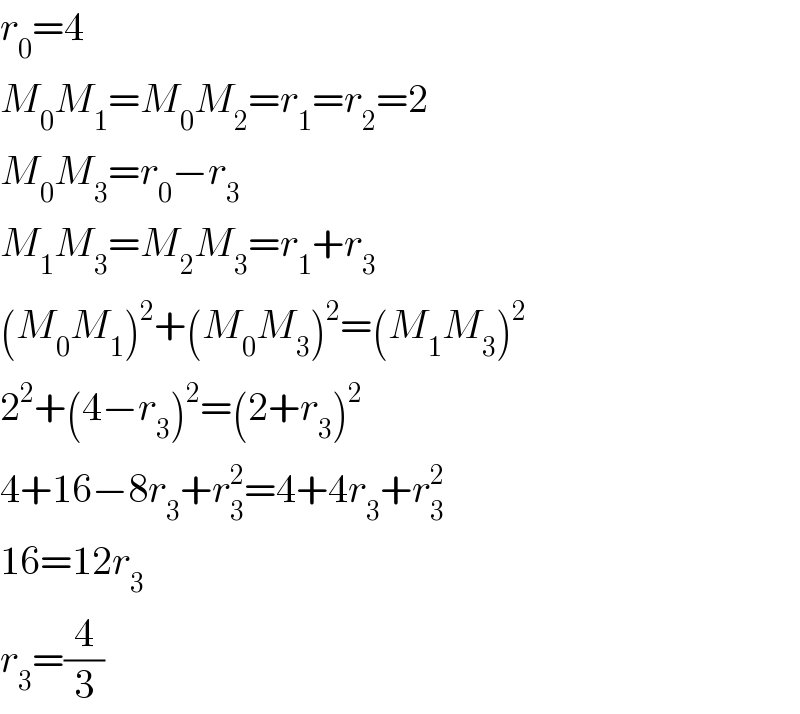
r_0 =4 M_0 M_1 =M_0 M_2 =r_1 =r_2 =2 M_0 M_3 =r_0 −r_3 M_1 M_3 =M_2 M_3 =r_1 +r_3 (M_0 M_1 )^2 +(M_0 M_3 )^2 =(M_1 M_3 )^2 2^2 +(4−r_3 )^2 =(2+r_3 )^2 4+16−8r_3 +r_3 ^2 =4+4r_3 +r_3 ^2 16=12r_3 r_3 =(4/3)

$${r}_{\mathrm{0}} =\mathrm{4} \\ $$$${M}_{\mathrm{0}} {M}_{\mathrm{1}} ={M}_{\mathrm{0}} {M}_{\mathrm{2}} ={r}_{\mathrm{1}} ={r}_{\mathrm{2}} =\mathrm{2} \\ $$$${M}_{\mathrm{0}} {M}_{\mathrm{3}} ={r}_{\mathrm{0}} −{r}_{\mathrm{3}} \\ $$$${M}_{\mathrm{1}} {M}_{\mathrm{3}} ={M}_{\mathrm{2}} {M}_{\mathrm{3}} ={r}_{\mathrm{1}} +{r}_{\mathrm{3}} \\ $$$$\left({M}_{\mathrm{0}} {M}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({M}_{\mathrm{0}} {M}_{\mathrm{3}} \right)^{\mathrm{2}} =\left({M}_{\mathrm{1}} {M}_{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{2}} +\left(\mathrm{4}−{r}_{\mathrm{3}} \right)^{\mathrm{2}} =\left(\mathrm{2}+{r}_{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\mathrm{4}+\mathrm{16}−\mathrm{8}{r}_{\mathrm{3}} +{r}_{\mathrm{3}} ^{\mathrm{2}} =\mathrm{4}+\mathrm{4}{r}_{\mathrm{3}} +{r}_{\mathrm{3}} ^{\mathrm{2}} \\ $$$$\mathrm{16}=\mathrm{12}{r}_{\mathrm{3}} \\ $$$${r}_{\mathrm{3}} =\frac{\mathrm{4}}{\mathrm{3}} \\ $$

Commented by Joel578 last updated on 09/May/18

$${what}\:{is}\:{M}\:? \\ $$

Commented by MJS last updated on 09/May/18

the centers of the circles. sorry, my language is German center is “Mittelpunkt” in German so without further thinking, M seemed natural...

$$\mathrm{the}\:\mathrm{centers}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circles}.\:\mathrm{sorry},\:\mathrm{my}\:\mathrm{language} \\ $$$$\mathrm{is}\:\mathrm{German}\:\mathrm{center}\:\mathrm{is}\:“\mathrm{Mittelpunkt}''\:\mathrm{in}\:\mathrm{German} \\ $$$$\mathrm{so}\:\mathrm{without}\:\mathrm{further}\:\mathrm{thinking},\:{M}\:\mathrm{seemed}\:\mathrm{natural}… \\ $$

Commented by Joel578 last updated on 10/May/18

$${okay},\:{thank}\:{you} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply