Question Number 34759 by Tinkutara last updated on 10/May/18

Answered by ajfour last updated on 10/May/18
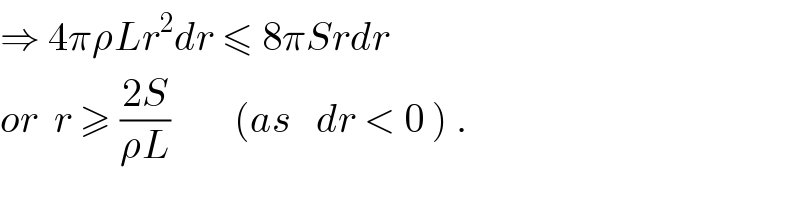
$$\Rightarrow\:\mathrm{4}\pi\rho{Lr}^{\mathrm{2}} {dr}\:\leqslant\:\mathrm{8}\pi{Srdr} \\ $$$${or}\:\:{r}\:\geqslant\:\frac{\mathrm{2}{S}}{\rho{L}}\:\:\:\:\:\:\:\:\left({as}\:\:\:{dr}\:<\:\mathrm{0}\:\right)\:. \\ $$
Commented by Tinkutara last updated on 11/May/18
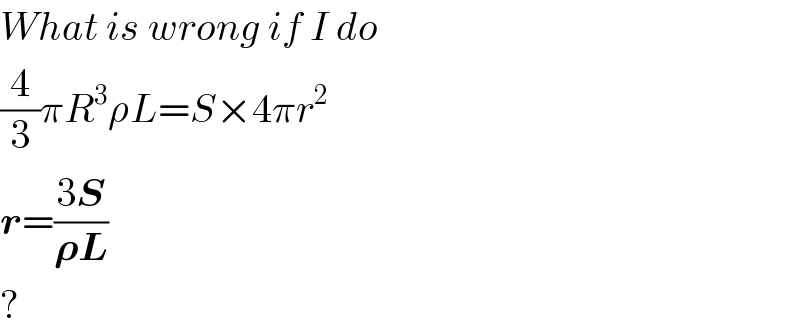
$${What}\:{is}\:{wrong}\:{if}\:{I}\:{do} \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}\pi{R}^{\mathrm{3}} \rho{L}={S}×\mathrm{4}\pi{r}^{\mathrm{2}} \\ $$$$\boldsymbol{{r}}=\frac{\mathrm{3}\boldsymbol{{S}}}{\boldsymbol{\rho{L}}} \\ $$$$? \\ $$
Commented by ajfour last updated on 11/May/18

$${process}\:{is}\:{continuous} \\ $$$${little}\:{energy}\:{required}\:{in}\:{a} \\ $$$${differential}\:{time}\:{interval}\:\:{dt} \\ $$$${for}\:{evaporation}\:{of}\:{a}\:{mass}\:{dm}\:{is} \\ $$$$\rho{L}\left(\mathrm{4}\pi{r}^{\mathrm{2}} \mid{dr}\mid\right)={loss}\:{in}\:{differential} \\ $$$${surface}\:{energy}\:=\:{S}\left(\mathrm{8}\pi{r}\mid{dr}\mid\right) \\ $$$$\left({the}\:{evaporation}\:{should}\:{take}\right. \\ $$$$\left.{place}\:{in}\:{each}\:{such}\:{time}\:{intervals}\right) \\ $$$${and}\:{tbis}\:{overall}\:{eq}.\:{of}\:{yours} \\ $$$${entire}\:{surface}\:{energy}\:=\:{entire} \\ $$$${energy}\:{requirement}\:{for}\:{evaporation} \\ $$$${isn}'{t}\:{correct}. \\ $$
Commented by Tinkutara last updated on 11/May/18
Can't we equate just initial and final conditions when the liquid drop evaporates completely?
Commented by ajfour last updated on 11/May/18

$${na}. \\ $$
Commented by Tinkutara last updated on 11/May/18
Thank you very much Sir! I got the answer. ��������
