Question Number 34781 by Tinkutara last updated on 11/May/18
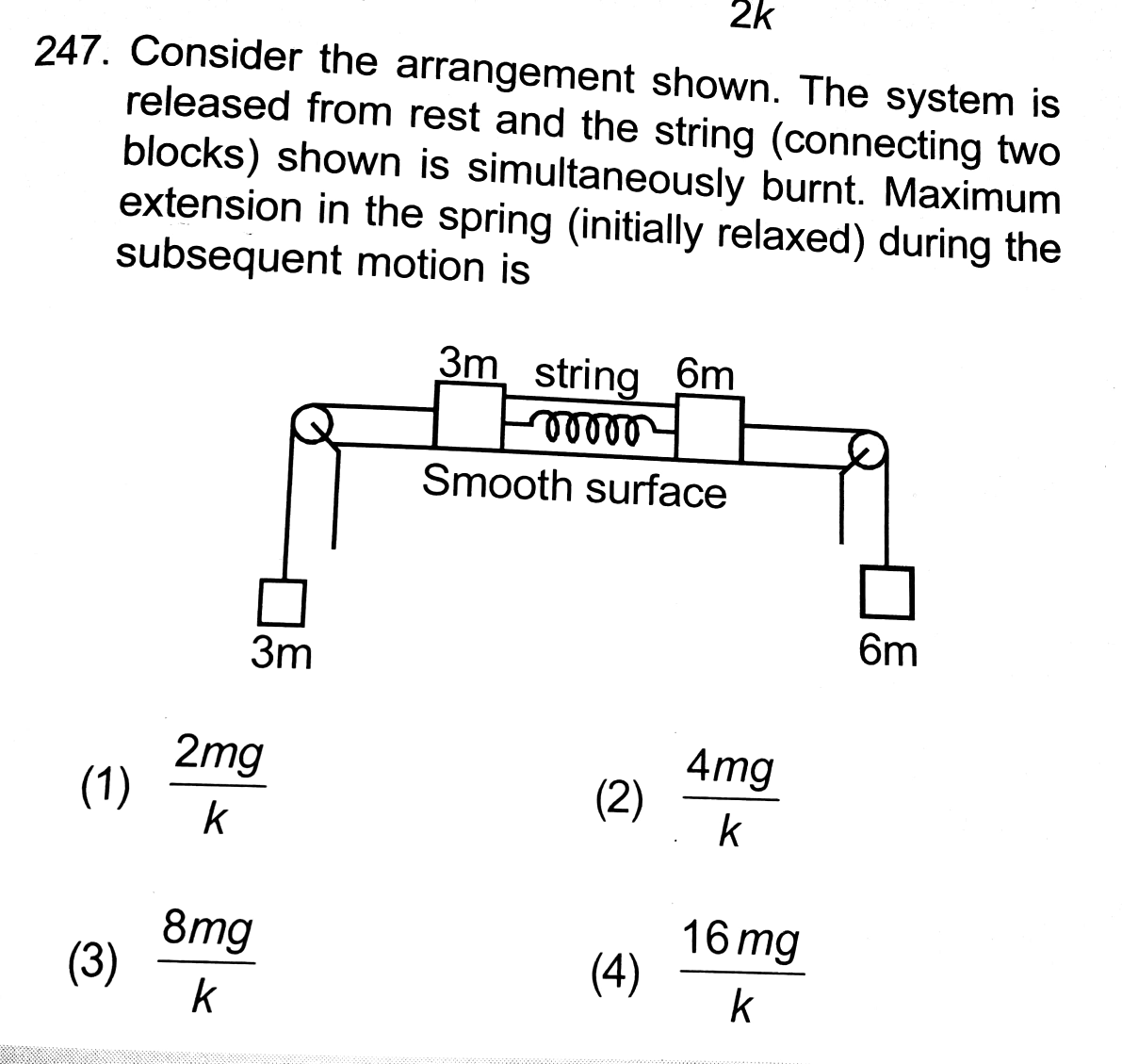
Answered by ajfour last updated on 11/May/18
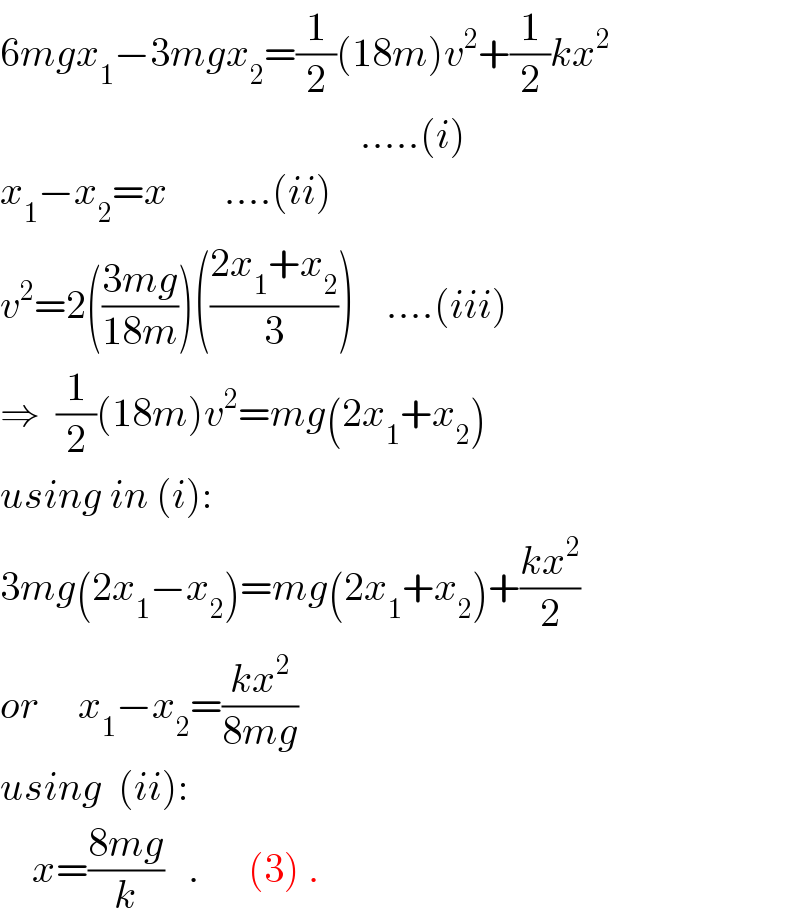
$$\mathrm{6}{mgx}_{\mathrm{1}} −\mathrm{3}{mgx}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{18}{m}\right){v}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{kx}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left({i}\right) \\ $$$${x}_{\mathrm{1}} −{x}_{\mathrm{2}} ={x}\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$${v}^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{3}{mg}}{\mathrm{18}{m}}\right)\left(\frac{\mathrm{2}{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }{\mathrm{3}}\right)\:\:\:\:….\left({iii}\right) \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{18}{m}\right){v}^{\mathrm{2}} ={mg}\left(\mathrm{2}{x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right) \\ $$$${using}\:{in}\:\left({i}\right): \\ $$$$\mathrm{3}{mg}\left(\mathrm{2}{x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)={mg}\left(\mathrm{2}{x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)+\frac{{kx}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${or}\:\:\:\:\:{x}_{\mathrm{1}} −{x}_{\mathrm{2}} =\frac{{kx}^{\mathrm{2}} }{\mathrm{8}{mg}} \\ $$$${using}\:\:\left({ii}\right): \\ $$$$\:\:\:\:{x}=\frac{\mathrm{8}{mg}}{{k}}\:\:\:.\:\:\:\:\:\:\left(\mathrm{3}\right)\:. \\ $$
Commented by Tinkutara last updated on 11/May/18
Please explain (iii) equation.
Commented by ajfour last updated on 11/May/18
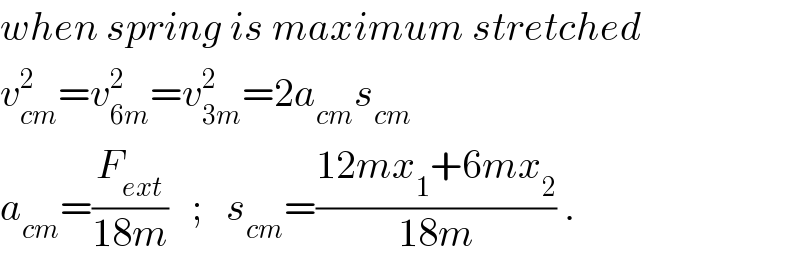
$${when}\:{spring}\:{is}\:{maximum}\:{stretched} \\ $$$${v}_{{cm}} ^{\mathrm{2}} ={v}_{\mathrm{6}{m}} ^{\mathrm{2}} ={v}_{\mathrm{3}{m}} ^{\mathrm{2}} =\mathrm{2}{a}_{{cm}} {s}_{{cm}} \\ $$$${a}_{{cm}} =\frac{{F}_{{ext}} }{\mathrm{18}{m}}\:\:\:;\:\:\:{s}_{{cm}} =\frac{\mathrm{12}{mx}_{\mathrm{1}} +\mathrm{6}{mx}_{\mathrm{2}} }{\mathrm{18}{m}}\:. \\ $$
Commented by Tinkutara last updated on 11/May/18
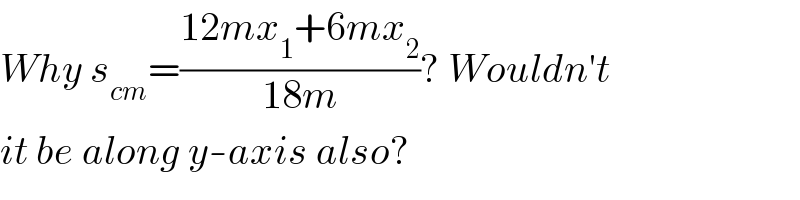
$${Why}\:{s}_{{cm}} =\frac{\mathrm{12}{mx}_{\mathrm{1}} +\mathrm{6}{mx}_{\mathrm{2}} }{\mathrm{18}{m}}?\:{Wouldn}'{t} \\ $$$${it}\:{be}\:{along}\:{y}-{axis}\:{also}? \\ $$
Commented by ajfour last updated on 11/May/18

$${yes}\:{y}_{{cm}\:} \neq\:\mathrm{0}\:,\:{but}\:{we}'{ll}\:{have}\:{to} \\ $$$${go}\:{into}\:{the}\:{normal}\:{reactions}\:{even}. \\ $$$${And}\:{as}\:{far}\:{as}\:{the}\:{displacement} \\ $$$${of}\:{centre}\:{of}\:{mass}\:{is}\:{concerned}, \\ $$$${we}\:{can}\:{assume}\:{the}\:{masses}\:\left(\mathrm{6}{m}\right)_{{s}} \\ $$$${and}\:\left(\mathrm{3}{m}\right)_{{s}} \:{have}\:{moved}\:{by}\:{x}_{\mathrm{1}} \:{and} \\ $$$${x}_{\mathrm{2}} \:{horizontally}.\:{situations}\:{are} \\ $$$${equivalent}\:{for}\:{obtaining}\:{s}_{{cm}} \:. \\ $$
Commented by Tinkutara last updated on 11/May/18
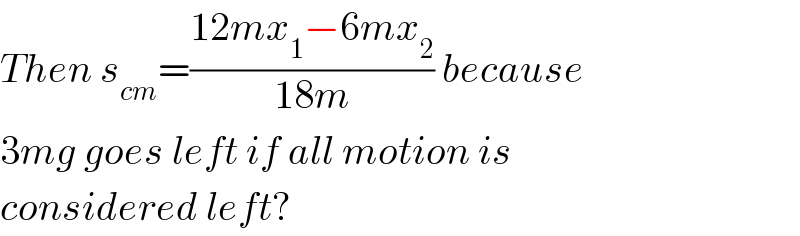
$${Then}\:{s}_{{cm}} =\frac{\mathrm{12}{mx}_{\mathrm{1}} −\mathrm{6}{mx}_{\mathrm{2}} }{\mathrm{18}{m}}\:{because} \\ $$$$\mathrm{3}{mg}\:{goes}\:{left}\:{if}\:{all}\:{motion}\:{is} \\ $$$${considered}\:{left}? \\ $$
Commented by ajfour last updated on 11/May/18
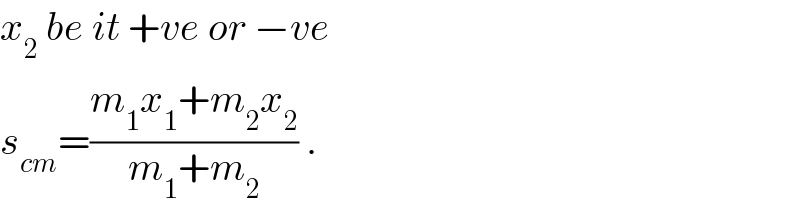
$${x}_{\mathrm{2}} \:{be}\:{it}\:+{ve}\:{or}\:−{ve} \\ $$$${s}_{{cm}} =\frac{{m}_{\mathrm{1}} {x}_{\mathrm{1}} +{m}_{\mathrm{2}} {x}_{\mathrm{2}} }{{m}_{\mathrm{1}} +{m}_{\mathrm{2}} }\:. \\ $$
Commented by Tinkutara last updated on 12/May/18
Thank you very much Sir! I got the answer. ��������
