Question Number 34850 by mondodotto@gmail.com last updated on 11/May/18

Answered by MJS last updated on 11/May/18
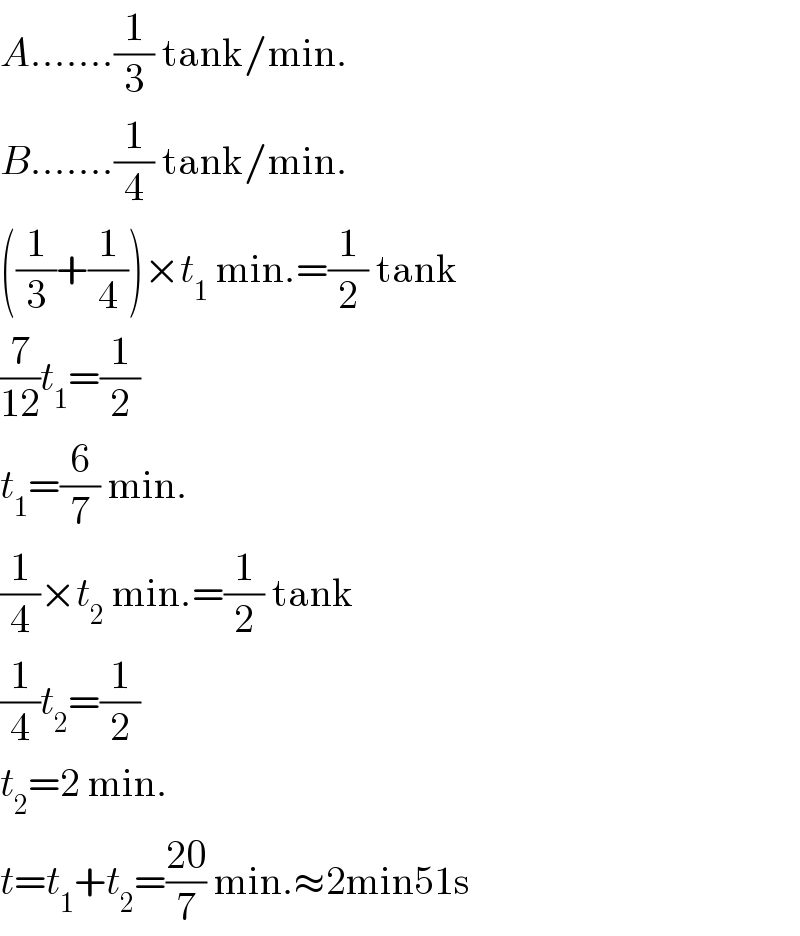
$${A}…….\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{tank}/\mathrm{min}. \\ $$$${B}…….\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{tank}/\mathrm{min}. \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}\right)×{t}_{\mathrm{1}} \:\mathrm{min}.=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{tank} \\ $$$$\frac{\mathrm{7}}{\mathrm{12}}{t}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${t}_{\mathrm{1}} =\frac{\mathrm{6}}{\mathrm{7}}\:\mathrm{min}. \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}×{t}_{\mathrm{2}} \:\mathrm{min}.=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{tank} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{t}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${t}_{\mathrm{2}} =\mathrm{2}\:\mathrm{min}. \\ $$$${t}={t}_{\mathrm{1}} +{t}_{\mathrm{2}} =\frac{\mathrm{20}}{\mathrm{7}}\:\mathrm{min}.\approx\mathrm{2min51s} \\ $$
Answered by candre last updated on 11/May/18
![let call the tank capacity T v_A =T/3 v_B =T/4 v(t)=(v_A +v_B )t [t min] ((T/3)+(T/4))t=(T/2) ((7T)/(12))t=(T/2) t=(T/2)∙((12)/(7T))=(6/7) the time B fills the half is v_B t=(T/2) t=(T/2)∙(4/T)=2 the total time is 2+(6/7)=((20)/7)≈2,85min ≈2min51,43s](https://www.tinkutara.com/question/Q34854.png)
$$\mathrm{let}\:\mathrm{call}\:\mathrm{the}\:\mathrm{tank}\:\mathrm{capacity}\:\mathrm{T} \\ $$$${v}_{{A}} ={T}/\mathrm{3} \\ $$$${v}_{{B}} ={T}/\mathrm{4} \\ $$$${v}\left({t}\right)=\left({v}_{{A}} +{v}_{{B}} \right){t}\:\:\:\left[{t}\:{min}\right] \\ $$$$\left(\frac{{T}}{\mathrm{3}}+\frac{{T}}{\mathrm{4}}\right){t}=\frac{{T}}{\mathrm{2}} \\ $$$$\frac{\mathrm{7}{T}}{\mathrm{12}}{t}=\frac{{T}}{\mathrm{2}} \\ $$$${t}=\frac{{T}}{\mathrm{2}}\centerdot\frac{\mathrm{12}}{\mathrm{7}{T}}=\frac{\mathrm{6}}{\mathrm{7}} \\ $$$$\mathrm{the}\:\mathrm{time}\:\mathrm{B}\:\mathrm{fills}\:\mathrm{the}\:\mathrm{half}\:\mathrm{is} \\ $$$${v}_{{B}} {t}=\frac{{T}}{\mathrm{2}} \\ $$$${t}=\frac{{T}}{\mathrm{2}}\centerdot\frac{\mathrm{4}}{{T}}=\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{total}\:\mathrm{time}\:\mathrm{is} \\ $$$$\mathrm{2}+\frac{\mathrm{6}}{\mathrm{7}}=\frac{\mathrm{20}}{\mathrm{7}}\approx\mathrm{2},\mathrm{85min} \\ $$$$\approx\mathrm{2min51},\mathrm{43}{s} \\ $$
