Question Number 34954 by ajfour last updated on 13/May/18
Commented by ajfour last updated on 13/May/18

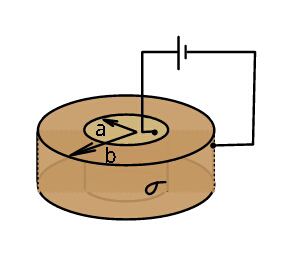
$${Find}\:{resistance}\:{of}\:{a}\:{cylindrical} \\ $$$${conductor}\:{of}\:{radius}\:\boldsymbol{{b}}\:{and}\:{thickness} \\ $$$$\boldsymbol{{t}}\:{with}\:{a}\:{concentric}\:{hole}\:{of}\:{radius} \\ $$$$\boldsymbol{{a}},\:{across}\:{its}\:{inner}\:{and}\:{outer} \\ $$$${surfaces}.\left({conductivity}\:\:{given}\:\sigma\:\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/May/18
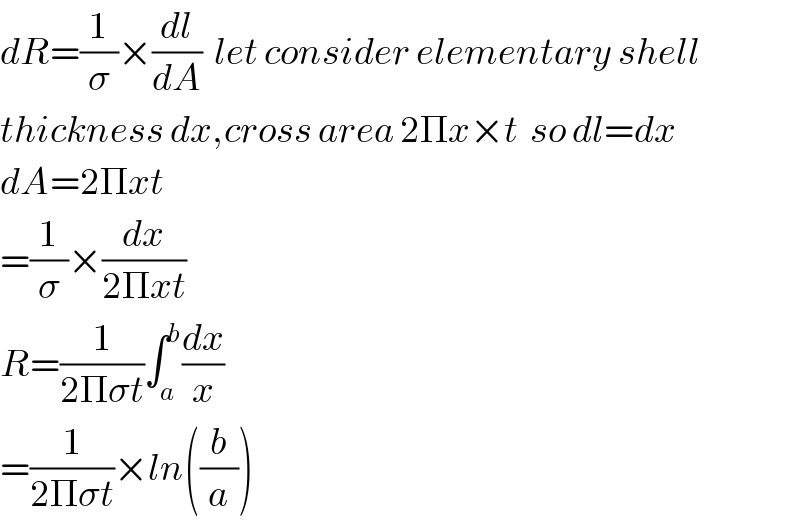
$${dR}=\frac{\mathrm{1}}{\sigma}×\frac{{dl}}{{dA}}\:\:{let}\:{consider}\:{elementary}\:{shell} \\ $$$${thickness}\:{dx},{cross}\:{area}\:\mathrm{2}\Pi{x}×{t}\:\:{so}\:{dl}={dx} \\ $$$${dA}=\mathrm{2}\Pi{xt} \\ $$$$=\frac{\mathrm{1}}{\sigma}×\frac{{dx}}{\mathrm{2}\Pi{xt}} \\ $$$${R}=\frac{\mathrm{1}}{\mathrm{2}\Pi\sigma{t}}\int_{{a}} ^{{b}} \frac{{dx}}{{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\Pi\sigma{t}}×{ln}\left(\frac{{b}}{{a}}\right) \\ $$
Commented by ajfour last updated on 13/May/18
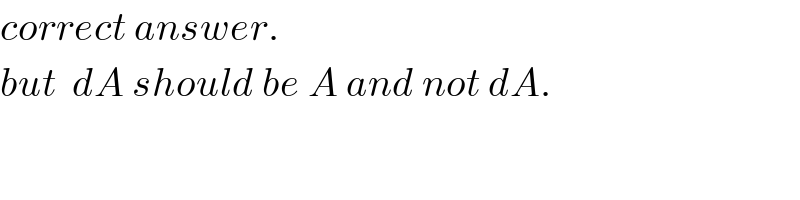
$${correct}\:{answer}. \\ $$$${but}\:\:{dA}\:{should}\:{be}\:{A}\:{and}\:{not}\:{dA}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/May/18

$${true}…{thanks}.. \\ $$
