Question-34956

Question Number 34956 by behi83417@gmail.com last updated on 13/May/18

Commented by a.i msup by abdo last updated on 13/May/18

changement (√x)=t give I = ∫_0 ^1 (t/(t^4 +t^2 +1)) 2tdt = 2∫_0 ^1 (t^2 /(t^4 +t^2 +1))dt ch. t=(1/u) I = −2∫_1 ^(+∞) (1/(u^2 ((1/u^4 ) +(1/u^2 ) +1)))(−(du/u^2 )) =2 ∫_1 ^(+∞) (du/(u^4 +u^2 +1)) 2I = 2{ ∫_0 ^1 ((t^2 )/(t^4 +t^2 +1))dt+∫_1 ^(+∞) (dt/(t^4 +t^2 +1))} ⇒ I = ∫_0 ^∞ ((1+t^2 )/(t^4 +t^2 +1))dt 2I = ∫_(−∞) ^(+∞) ((1+t^2 )/(t^4 +t^2 +1))dt let consider the complex function ϕ(z) = ((1+z^2 )/(z^4 +z^2 +1)) poles of ϕ?

$${changement}\:\sqrt{{x}}={t}\:{give} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{t}}{{t}^{\mathrm{4}} \:+{t}^{\mathrm{2}} \:+\mathrm{1}}\:\mathrm{2}{tdt} \\ $$$$=\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:+{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:{ch}.\:{t}=\frac{\mathrm{1}}{{u}} \\ $$$${I}\:=\:−\mathrm{2}\int_{\mathrm{1}} ^{+\infty} \:\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{u}^{\mathrm{4}} }\:+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\:+\mathrm{1}\right)}\left(−\frac{{du}}{{u}^{\mathrm{2}} }\right) \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\:\:\:\frac{{du}}{{u}^{\mathrm{4}} \:+{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{2}{I}\:=\:\mathrm{2}\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{t}^{\mathrm{2}} \:}{{t}^{\mathrm{4}} \:+{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}+\int_{\mathrm{1}} ^{+\infty} \:\frac{{dt}}{{t}^{\mathrm{4}} \:+{t}^{\mathrm{2}} \:+\mathrm{1}}\right\} \\ $$$$\Rightarrow\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:+{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$\mathrm{2}{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:+{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$${let}\:{consider}\:{the}\:{complex}\:{function} \\ $$$$\varphi\left({z}\right)\:=\:\frac{\mathrm{1}+{z}^{\mathrm{2}} }{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:{poles}\:{of}\:\varphi? \\ $$

Commented by abdo mathsup 649 cc last updated on 13/May/18

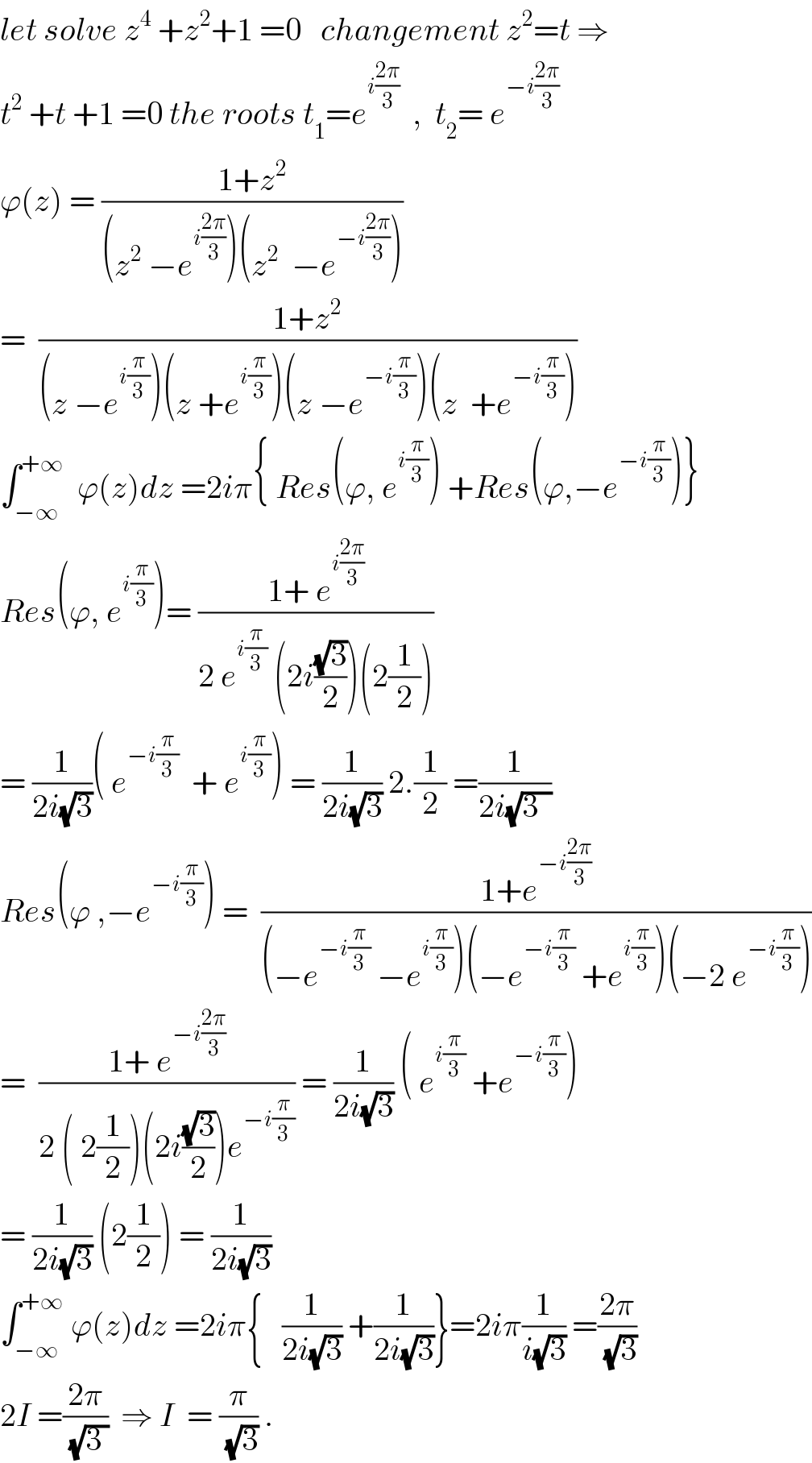
let solve z^4 +z^2 +1 =0 changement z^2 =t ⇒ t^2 +t +1 =0 the roots t_1 =e^(i((2π)/3)) , t_2 = e^(−i((2π)/3)) ϕ(z) = ((1+z^2 )/((z^2 −e^(i((2π)/3)) )(z^2 −e^(−i((2π)/3)) ))) = ((1+z^2 )/((z −e^(i(π/3)) )(z +e^(i(π/3)) )(z −e^(−i(π/3)) )(z +e^(−i(π/3)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ, e^(i(π/3)) ) +Res(ϕ,−e^(−i(π/3)) )} Res(ϕ, e^(i(π/3)) )= ((1+ e^(i((2π)/3)) )/(2 e^(i(π/3)) (2i((√3)/2))(2(1/2)))) = (1/(2i(√3)))( e^(−i(π/3)) + e^(i(π/3)) ) = (1/(2i(√3))) 2.(1/2) =(1/(2i(√(3 )))) Res(ϕ ,−e^(−i(π/3)) ) = ((1+e^(−i((2π)/3)) )/((−e^(−i(π/3)) −e^(i(π/3)) )(−e^(−i(π/3)) +e^(i(π/3)) )(−2 e^(−i(π/3)) ))) = ((1+ e^(−i((2π)/3)) )/(2 ( 2(1/2))(2i((√3)/2))e^(−i(π/3)) )) = (1/(2i(√3))) ( e^(i(π/3)) +e^(−i(π/3)) ) = (1/(2i(√3))) (2(1/2)) = (1/(2i(√3))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ (1/(2i(√3))) +(1/(2i(√3)))}=2iπ(1/(i(√3))) =((2π)/( (√3))) 2I =((2π)/( (√(3 )))) ⇒ I = (π/( (√3))) .

$${let}\:{solve}\:{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} +\mathrm{1}\:=\mathrm{0}\:\:\:{changement}\:{z}^{\mathrm{2}} ={t}\:\Rightarrow \\ $$$${t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}\:=\mathrm{0}\:{the}\:{roots}\:{t}_{\mathrm{1}} ={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:,\:\:{t}_{\mathrm{2}} =\:{e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$\varphi\left({z}\right)\:=\:\frac{\mathrm{1}+{z}^{\mathrm{2}} }{\left({z}^{\mathrm{2}} \:−{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} \:\:−{e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)} \\ $$$$=\:\:\frac{\mathrm{1}+{z}^{\mathrm{2}} }{\left({z}\:−{e}^{{i}\frac{\pi}{\mathrm{3}}} \right)\left({z}\:+{e}^{{i}\frac{\pi}{\mathrm{3}}} \right)\left({z}\:−{e}^{−{i}\frac{\pi}{\mathrm{3}}} \right)\left({z}\:\:+{e}^{−{i}\frac{\pi}{\mathrm{3}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,\:{e}^{{i}\frac{\pi}{\mathrm{3}}} \right)\:+{Res}\left(\varphi,−{e}^{−{i}\frac{\pi}{\mathrm{3}}} \right)\right\} \\ $$$${Res}\left(\varphi,\:{e}^{{i}\frac{\pi}{\mathrm{3}}} \right)=\:\frac{\mathrm{1}+\:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} }{\mathrm{2}\:{e}^{{i}\frac{\pi}{\mathrm{3}}} \:\left(\mathrm{2}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left(\:{e}^{−{i}\frac{\pi}{\mathrm{3}}} \:\:+\:{e}^{{i}\frac{\pi}{\mathrm{3}}} \right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}\:\:}} \\ $$$${Res}\left(\varphi\:,−{e}^{−{i}\frac{\pi}{\mathrm{3}}} \right)\:=\:\:\frac{\mathrm{1}+{e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} }{\left(−{e}^{−{i}\frac{\pi}{\mathrm{3}}} \:−{e}^{{i}\frac{\pi}{\mathrm{3}}} \right)\left(−{e}^{−{i}\frac{\pi}{\mathrm{3}}} \:+{e}^{{i}\frac{\pi}{\mathrm{3}}} \right)\left(−\mathrm{2}\:{e}^{−{i}\frac{\pi}{\mathrm{3}}} \right)} \\ $$$$=\:\:\frac{\mathrm{1}+\:{e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} }{\mathrm{2}\:\left(\:\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{2}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right){e}^{−{i}\frac{\pi}{\mathrm{3}}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:\left(\:{e}^{{i}\frac{\pi}{\mathrm{3}}} \:+{e}^{−{i}\frac{\pi}{\mathrm{3}}} \right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:\left(\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\:\:\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\right\}=\mathrm{2}{i}\pi\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}\:=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{2}{I}\:=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}\:}}\:\:\Rightarrow\:{I}\:\:=\:\frac{\pi}{\:\sqrt{\mathrm{3}}}\:. \\ $$

Answered by ajfour last updated on 13/May/18

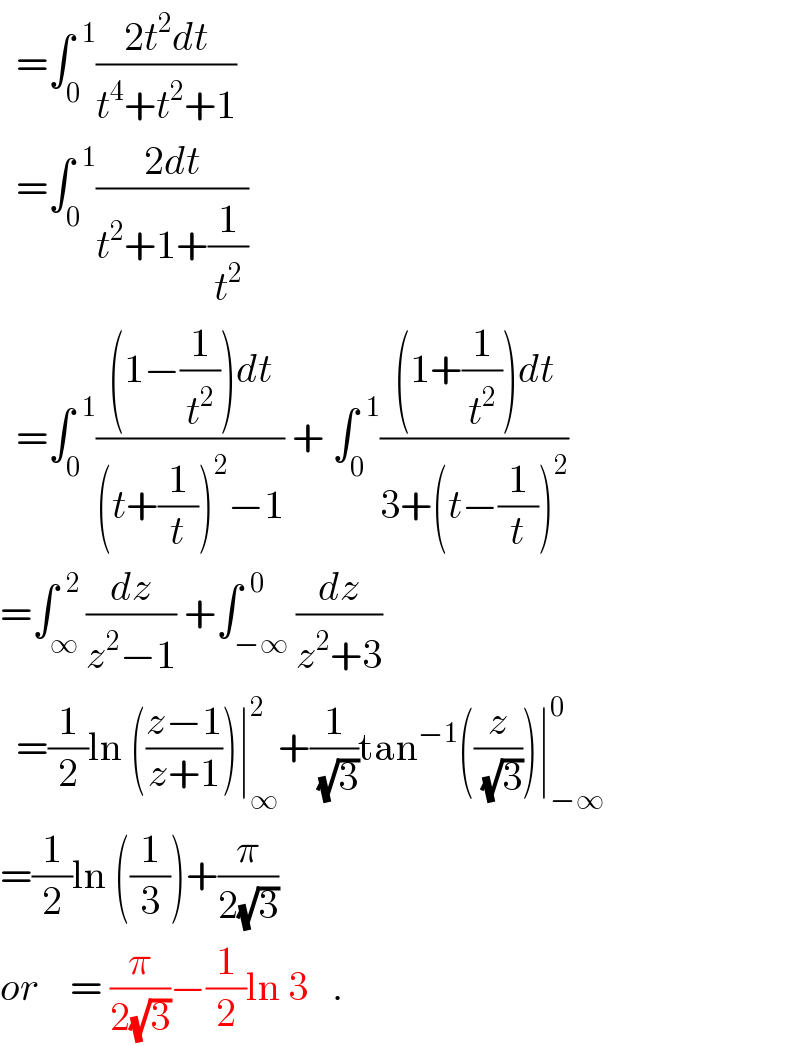
=∫_0 ^( 1) ((2t^2 dt)/(t^4 +t^2 +1)) =∫_0 ^( 1) ((2dt)/(t^2 +1+(1/t^2 ))) =∫_0 ^( 1) (((1−(1/t^2 ))dt)/((t+(1/t))^2 −1)) + ∫_0 ^( 1) (((1+(1/t^2 ))dt)/(3+(t−(1/t))^2 )) =∫_∞ ^( 2) (dz/(z^2 −1)) +∫_(−∞) ^( 0) (dz/(z^2 +3)) =(1/2)ln (((z−1)/(z+1)))∣_∞ ^2 +(1/( (√3)))tan^(−1) ((z/( (√3))))∣_(−∞) ^0 =(1/2)ln ((1/3))+(π/(2(√3))) or = (π/(2(√3)))−(1/2)ln 3 .

$$\:\:=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\mathrm{2}{t}^{\mathrm{2}} {dt}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\:\: \\ $$$$\:\:=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){dt}}{\left({t}+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} −\mathrm{1}}\:+\:\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){dt}}{\mathrm{3}+\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} } \\ $$$$=\int_{\infty} ^{\:\:\mathrm{2}} \frac{{dz}}{{z}^{\mathrm{2}} −\mathrm{1}}\:+\int_{−\infty} ^{\:\:\mathrm{0}} \frac{{dz}}{{z}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\frac{{z}−\mathrm{1}}{{z}+\mathrm{1}}\right)\mid_{\infty} ^{\mathrm{2}} +\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{z}}{\:\sqrt{\mathrm{3}}}\right)\mid_{−\infty} ^{\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\: \\ $$$${or}\:\:\:\:=\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{3}\:\:\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 13/May/18

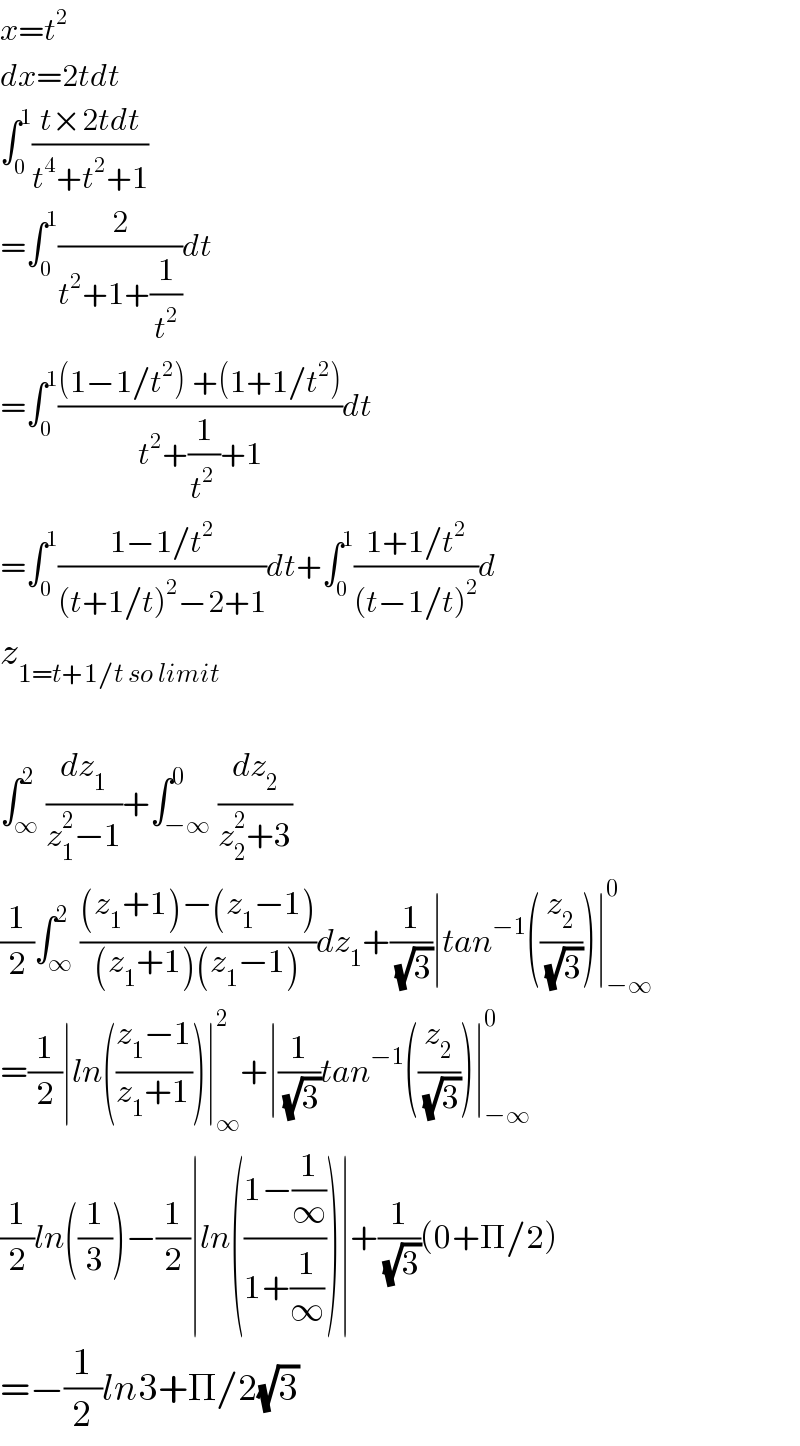
x=t^2 dx=2tdt ∫_0 ^1 ((t×2tdt)/(t^4 +t^2 +1)) =∫_0 ^1 (2/(t^2 +1+(1/t^2 )))dt =∫_0 ^1 (((1−1/t^2 ) +(1+1/t^2 ))/(t^2 +(1/t^(2 ) )+1))dt =∫_0 ^1 ((1−1/t^2 )/((t+1/t)^2 −2+1))dt+∫_0 ^1 ((1+1/t^2 )/((t−1/t)^2 ))d z_(1=t+1/t so limit) ∫_∞ ^2 (dz_1 /(z_1 ^2 −1))+∫_(−∞) ^0 (dz_2 /(z_2 ^2 +3)) (1/2)∫_∞ ^2 (((z_1 +1)−(z_1 −1))/((z_1 +1)(z_1 −1)))dz_1 +(1/( (√3)))∣tan^(−1) ((z_2 /( (√3))))∣_(−∞) ^0 =(1/2)∣ln(((z_1 −1)/(z_1 +1)))∣_∞ ^2 +∣(1/( (√3)))tan^(−1) ((z_2 /( (√3))))∣_(−∞) ^0 (1/2)ln((1/3))−(1/2)∣ln(((1−(1/∞))/(1+(1/∞))))∣+(1/( (√3)))(0+Π/2) =−(1/2)ln3+Π/2(√3)

$${x}={t}^{\mathrm{2}} \\ $$$${dx}=\mathrm{2}{tdt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}×\mathrm{2}{tdt}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}}{{t}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{1}/{t}^{\mathrm{2}} \right)\:+\left(\mathrm{1}+\mathrm{1}/{t}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}\:} }+\mathrm{1}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\mathrm{1}/{t}^{\mathrm{2}} }{\left({t}+\mathrm{1}/{t}\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{1}}{dt}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+\mathrm{1}/{t}^{\mathrm{2}} }{\left({t}−\mathrm{1}/{t}\right)^{\mathrm{2}} }{d} \\ $$$${z}_{\mathrm{1}={t}+\mathrm{1}/{t}\:{so}\:{limit}} \: \\ $$$$ \\ $$$$\int_{\infty} ^{\mathrm{2}} \frac{{dz}_{\mathrm{1}} }{{z}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}}+\int_{−\infty} ^{\mathrm{0}} \frac{{dz}_{\mathrm{2}} }{{z}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\infty} ^{\mathrm{2}} \frac{\left({z}_{\mathrm{1}} +\mathrm{1}\right)−\left({z}_{\mathrm{1}} −\mathrm{1}\right)}{\left({z}_{\mathrm{1}} +\mathrm{1}\right)\left({z}_{\mathrm{1}} −\mathrm{1}\right)}{dz}_{\mathrm{1}} +\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{z}_{\mathrm{2}} }{\:\sqrt{\mathrm{3}}}\right)\mid_{−\infty} ^{\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mid{ln}\left(\frac{{z}_{\mathrm{1}} −\mathrm{1}}{{z}_{\mathrm{1}} +\mathrm{1}}\right)\mid_{\infty} ^{\mathrm{2}} +\mid\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{z}_{\mathrm{2}} }{\:\sqrt{\mathrm{3}}}\right)\mid_{−\infty} ^{\mathrm{0}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mid{ln}\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{\infty}}{\mathrm{1}+\frac{\mathrm{1}}{\infty}}\right)\mid+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{0}+\Pi/\mathrm{2}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{3}+\Pi/\mathrm{2}\sqrt{\mathrm{3}} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 13/May/18

$${true}… \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 13/May/18

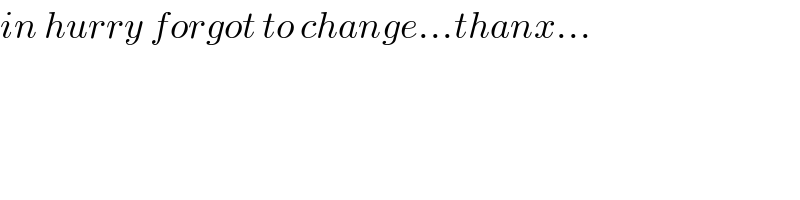
$${in}\:{hurry}\:{forgot}\:{to}\:{change}…{thanx}… \\ $$

Answered by MJS last updated on 13/May/18

∫((√x)/(x^2 +x+1))dx= [u=(√x) → dx=2(√x)du] =2∫(u^2 /(u^4 +u^2 +1))du=2∫(u^2 /((u^2 −u+1)(u^2 +u+1)))du= =2∫((u/(2(u^2 −u+1)))−(u/(2(u^2 +u+1))))du= =∫(u/(u^2 −u+1))du−∫(u/(u^2 +u+1))du= =∫(((2u−1)/(2(u^2 −u+1)))+(1/(2(u^2 −u+1))))du−∫(((2u+1)/(2(u^2 +u+1)))−(1/(2(u^2 +u+1))))du= =(1/2)(∫((2u−1)/(u^2 −u+1))du+∫(1/(u^2 −u+1))du−∫((2u+1)/(u^2 +u+1))du+∫(1/(u^2 +u+1))du)= ∫((2u±1)/(u^2 ±u+1))du= [v=u^2 ±u+1 → du=(dv/(2u±1))] =∫(1/v)dv=ln ∣v∣=ln ∣u^2 ±u+1∣ ∫(1/(u^2 ±u+1))du=∫(1/((u±(1/2))^2 +(3/4)))du= [v=((√3)/3)(2u±1) → du=((√3)/2)dv] ((2(√3))/3)∫(1/(v^2 +1))dv=((2(√3))/3)arctan v=((2(√3))/3)arctan ((√3)/3)(2u±1) =(1/2)(ln ∣u^2 −u+1∣+((2(√3))/3)arctan ((√3)/3)(2u−1)−ln ∣u^2 +u+1∣+((2(√3))/3)arctan ((√3)/3)(2u+1))= =((ln ∣x−(√x)+1∣−ln ∣x+(√x)+1∣)/2)+((√3)/3)(arctan ((√3)/3)(2(√x)−1)+arcran ((√3)/3)(2(√x)+1)) ∫_0 ^1 ((√x)/(x^2 +x+1))dx=((√3)/6)π−(1/2)ln 3

$$\int\frac{\sqrt{{x}}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}}{du}\right] \\ $$$$=\mathrm{2}\int\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{4}} +{u}^{\mathrm{2}} +\mathrm{1}}{du}=\mathrm{2}\int\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} −{u}+\mathrm{1}\right)\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)}{du}= \\ $$$$=\mathrm{2}\int\left(\frac{{u}}{\mathrm{2}\left({u}^{\mathrm{2}} −{u}+\mathrm{1}\right)}−\frac{{u}}{\mathrm{2}\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)}\right){du}= \\ $$$$=\int\frac{{u}}{{u}^{\mathrm{2}} −{u}+\mathrm{1}}{du}−\int\frac{{u}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}}{du}= \\ $$$$=\int\left(\frac{\mathrm{2}{u}−\mathrm{1}}{\mathrm{2}\left({u}^{\mathrm{2}} −{u}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left({u}^{\mathrm{2}} −{u}+\mathrm{1}\right)}\right){du}−\int\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\mathrm{2}\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)}\right){du}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\int\frac{\mathrm{2}{u}−\mathrm{1}}{{u}^{\mathrm{2}} −{u}+\mathrm{1}}{du}+\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} −{u}+\mathrm{1}}{du}−\int\frac{\mathrm{2}{u}+\mathrm{1}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}}{du}+\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}}{du}\right)= \\ $$$$\:\:\:\:\:\:\:\:\:\:\int\frac{\mathrm{2}{u}\pm\mathrm{1}}{{u}^{\mathrm{2}} \pm{u}+\mathrm{1}}{du}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{v}={u}^{\mathrm{2}} \pm{u}+\mathrm{1}\:\rightarrow\:{du}=\frac{{dv}}{\mathrm{2}{u}\pm\mathrm{1}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\int\frac{\mathrm{1}}{{v}}{dv}=\mathrm{ln}\:\mid{v}\mid=\mathrm{ln}\:\mid{u}^{\mathrm{2}} \pm{u}+\mathrm{1}\mid \\ $$$$\:\:\:\:\:\:\:\:\:\:\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} \pm{u}+\mathrm{1}}{du}=\int\frac{\mathrm{1}}{\left({u}\pm\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}{du}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{v}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{u}\pm\mathrm{1}\right)\:\rightarrow\:{du}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dv}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{\mathrm{1}}{{v}^{\mathrm{2}} +\mathrm{1}}{dv}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:{v}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{u}\pm\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\:\mid{u}^{\mathrm{2}} −{u}+\mathrm{1}\mid+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{u}−\mathrm{1}\right)−\mathrm{ln}\:\mid{u}^{\mathrm{2}} +{u}+\mathrm{1}\mid+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{u}+\mathrm{1}\right)\right)= \\ $$$$=\frac{\mathrm{ln}\:\mid{x}−\sqrt{{x}}+\mathrm{1}\mid−\mathrm{ln}\:\mid{x}+\sqrt{{x}}+\mathrm{1}\mid}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}\sqrt{{x}}−\mathrm{1}\right)+\mathrm{arcran}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}\sqrt{{x}}+\mathrm{1}\right)\right) \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\sqrt{{x}}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\pi−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{3} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply