Question Number 34985 by NECx last updated on 14/May/18
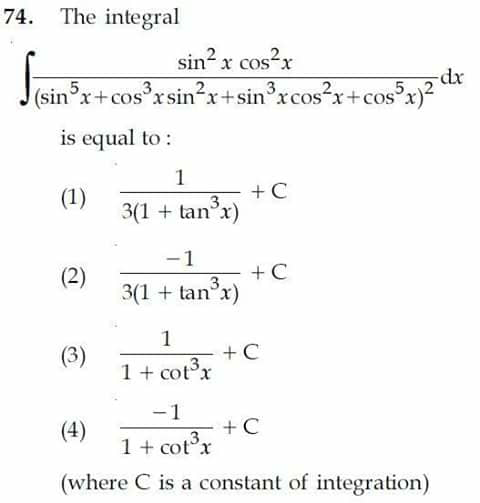
Answered by ajfour last updated on 14/May/18

$${Dividing}\:{numerator}\:{and}\:{Denominator} \\ $$$${by}\:\mathrm{cos}\:^{\mathrm{10}} {x}\:\:{we}\:{get} \\ $$$$=\int\frac{\mathrm{tan}\:^{\mathrm{2}} {x}\left(\mathrm{sec}\:^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{\left(\mathrm{tan}\:^{\mathrm{5}} {x}+\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{tan}\:^{\mathrm{3}} {x}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{sec}\:^{\mathrm{2}} {xdx} \\ $$$$=\int\frac{{t}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} {dt}}{\left({t}^{\mathrm{5}} +{t}^{\mathrm{3}} +{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\:\:\:\:\:\:\:\left(\forall\:{t}=\mathrm{tan}\:{x}\right) \\ $$$$ \\ $$$$\:=\int\frac{{t}^{\mathrm{2}} {dt}}{\left(\mathrm{1}+{t}^{\mathrm{3}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{3}}\left(−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{3}} {x}}\right)+{c} \\ $$$${So}\:\:\left(\mathrm{2}\right). \\ $$
Commented by NECx last updated on 14/May/18
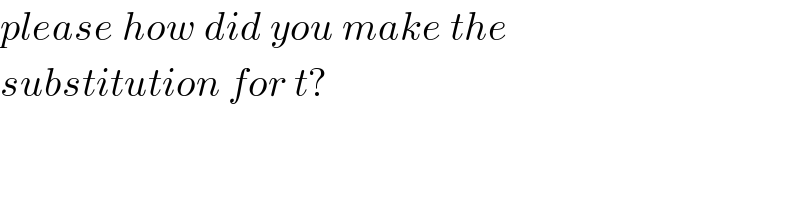
$${please}\:{how}\:{did}\:{you}\:{make}\:{the} \\ $$$${substitution}\:{for}\:{t}? \\ $$
Commented by NECx last updated on 14/May/18
$${Thank}\:{you}\:{so}\:{much}\: \\ $$
