Menu Close

Question-35124

Tinku Tara 0 Comments
Pin




Question Number 35124 by Tinkutara last updated on 15/May/18
Commented by Tinkutara last updated on 15/May/18
It contains no α?
$${It}\:{contains}\:{no}\:\alpha? \\ $$
Commented by Tinkutara last updated on 15/May/18
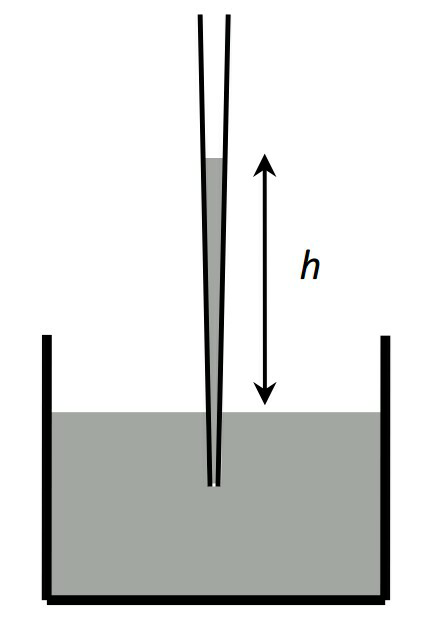
Commented by ajfour last updated on 15/May/18
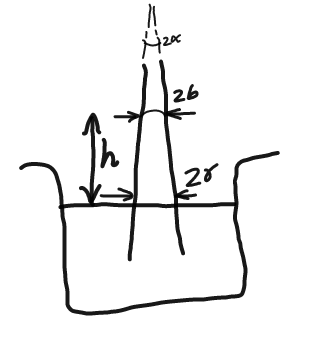
Commented by ajfour last updated on 16/May/18
S(2πb)cos θ = (π/3){r^2 (h+y)−b^2 y}ρg ((h+y)/r) = (y/b) = (1/(tan α)) ⇒ r=b+htan α ⇒ S(2πb)cos (θ+α)=(π/(3tan α)){r^3 −b^3 }ρg r^3 =((6bStan αcos (θ+α))/(ρg))+b^3 h=(1/(tan α)){(((6bStan αcos (θ+α))/(ρg))+b^3 )^(1/3) −b} . if S is small , α is small too, then h=(b/(tan α)){1+(1/3)×((6Stan αcos (θ+α))/(b^2 ρg))−1} = ((2Scos (θ+α))/(ρgb)) . I have taken the apex angle to be 2α. If apex angle is α (as in your question) the answer indeed is then : h=((2Scos (𝛉+(𝛂/2)))/(𝛒bg)) .
$${S}\left(\mathrm{2}\pi{b}\right)\mathrm{cos}\:\theta\:=\:\frac{\pi}{\mathrm{3}}\left\{{r}^{\mathrm{2}} \left({h}+{y}\right)−{b}^{\mathrm{2}} {y}\right\}\rho{g} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{h}+{y}}{{r}}\:=\:\frac{{y}}{{b}}\:=\:\frac{\mathrm{1}}{\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow\:\:\:{r}={b}+{h}\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\:{S}\left(\mathrm{2}\pi{b}\right)\mathrm{cos}\:\left(\theta+\alpha\right)=\frac{\pi}{\mathrm{3tan}\:\alpha}\left\{{r}^{\mathrm{3}} −{b}^{\mathrm{3}} \right\}\rho{g} \\ $$$${r}^{\mathrm{3}} =\frac{\mathrm{6}{bS}\mathrm{tan}\:\alpha\mathrm{cos}\:\left(\theta+\alpha\right)}{\rho{g}}+{b}^{\mathrm{3}} \\ $$$$\boldsymbol{{h}}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}\left\{\left(\frac{\mathrm{6}{bS}\mathrm{tan}\:\alpha\mathrm{cos}\:\left(\theta+\alpha\right)}{\rho{g}}+{b}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} −{b}\right\}\:. \\ $$$${if}\:{S}\:{is}\:{small}\:,\:\alpha\:{is}\:{small}\:{too},\:{then} \\ $$$$\:\:\:\:\boldsymbol{{h}}=\frac{{b}}{\mathrm{tan}\:\alpha}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{6}{S}\mathrm{tan}\:\alpha\mathrm{cos}\:\left(\theta+\alpha\right)}{{b}^{\mathrm{2}} \rho{g}}−\mathrm{1}\right\} \\ $$$$\:\:\:=\:\frac{\mathrm{2}{S}\mathrm{cos}\:\left(\theta+\alpha\right)}{\rho{gb}}\:. \\ $$$${I}\:{have}\:{taken}\:{the}\:{apex}\:{angle}\:{to}\:{be} \\ $$$$\mathrm{2}\alpha.\:{If}\:{apex}\:{angle}\:{is}\:\alpha\:\left({as}\:{in}\:{your}\right. \\ $$$$\left.{question}\right)\:{the}\:{answer}\:{indeed}\:{is} \\ $$$${then}\:\:\::\:\:\:\boldsymbol{{h}}=\frac{\mathrm{2}\boldsymbol{{S}}\mathrm{cos}\:\left(\boldsymbol{\theta}+\frac{\boldsymbol{\alpha}}{\mathrm{2}}\right)}{\boldsymbol{\rho{bg}}}\:. \\ $$
Commented by Tinkutara last updated on 16/May/18
Answer given is dependent on alpha.
Commented by ajfour last updated on 16/May/18
post the answer please.
$${post}\:{the}\:{answer}\:{please}. \\ $$
Commented by Tinkutara last updated on 16/May/18
Question from JEE Advanced 2014.
Commented by ajfour last updated on 16/May/18
i compared the capillary in the diagrams now only, sorry for the reverse orientation, however my answer for h is the same !
$${i}\:{compared}\:{the}\:{capillary}\:{in}\:{the} \\ $$$${diagrams}\:{now}\:{only},\:{sorry}\:{for} \\ $$$${the}\:{reverse}\:{orientation},\:{however} \\ $$$${my}\:{answer}\:{for}\:\boldsymbol{{h}}\:{is}\:{the}\:{same}\:! \\ $$
Commented by Tinkutara last updated on 16/May/18
I appreciate your solution Sir!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *