Question Number 35167 by behi83417@gmail.com last updated on 16/May/18
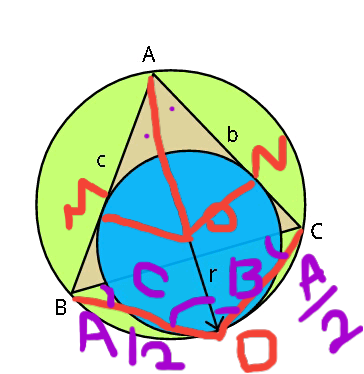
Commented by behi83417@gmail.com last updated on 16/May/18
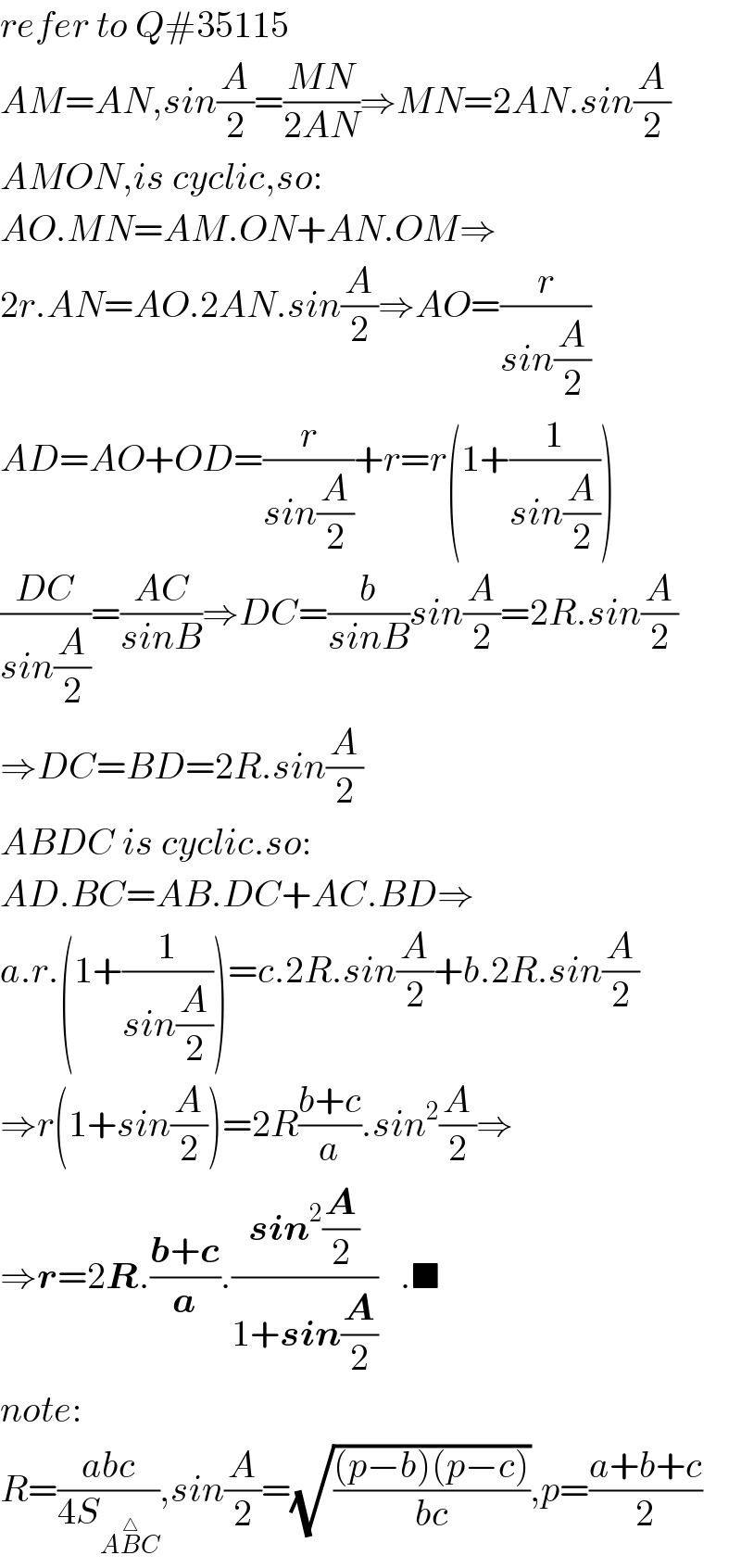
$${refer}\:{to}\:{Q}#\mathrm{35115} \\ $$$${AM}={AN},{sin}\frac{{A}}{\mathrm{2}}=\frac{{MN}}{\mathrm{2}{AN}}\Rightarrow{MN}=\mathrm{2}{AN}.{sin}\frac{{A}}{\mathrm{2}} \\ $$$${AMON},{is}\:{cyclic},{so}: \\ $$$${AO}.{MN}={AM}.{ON}+{AN}.{OM}\Rightarrow \\ $$$$\mathrm{2}{r}.{AN}={AO}.\mathrm{2}{AN}.{sin}\frac{{A}}{\mathrm{2}}\Rightarrow{AO}=\frac{{r}}{{sin}\frac{{A}}{\mathrm{2}}} \\ $$$${AD}={AO}+{OD}=\frac{{r}}{{sin}\frac{{A}}{\mathrm{2}}}+{r}={r}\left(\mathrm{1}+\frac{\mathrm{1}}{{sin}\frac{{A}}{\mathrm{2}}}\right) \\ $$$$\frac{{DC}}{{sin}\frac{{A}}{\mathrm{2}}}=\frac{{AC}}{{sinB}}\Rightarrow{DC}=\frac{{b}}{{sinB}}{sin}\frac{{A}}{\mathrm{2}}=\mathrm{2}{R}.{sin}\frac{{A}}{\mathrm{2}} \\ $$$$\Rightarrow{DC}={BD}=\mathrm{2}{R}.{sin}\frac{{A}}{\mathrm{2}} \\ $$$${ABDC}\:{is}\:{cyclic}.{so}: \\ $$$${AD}.{BC}={AB}.{DC}+{AC}.{BD}\Rightarrow \\ $$$${a}.{r}.\left(\mathrm{1}+\frac{\mathrm{1}}{{sin}\frac{{A}}{\mathrm{2}}}\right)={c}.\mathrm{2}{R}.{sin}\frac{{A}}{\mathrm{2}}+{b}.\mathrm{2}{R}.{sin}\frac{{A}}{\mathrm{2}} \\ $$$$\Rightarrow{r}\left(\mathrm{1}+{sin}\frac{{A}}{\mathrm{2}}\right)=\mathrm{2}{R}\frac{{b}+{c}}{{a}}.{sin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}\Rightarrow \\ $$$$\Rightarrow\boldsymbol{{r}}=\mathrm{2}\boldsymbol{{R}}.\frac{\boldsymbol{{b}}+\boldsymbol{{c}}}{\boldsymbol{{a}}}.\frac{\boldsymbol{{sin}}^{\mathrm{2}} \frac{\boldsymbol{{A}}}{\mathrm{2}}}{\mathrm{1}+\boldsymbol{{sin}}\frac{\boldsymbol{{A}}}{\mathrm{2}}}\:\:\:.\blacksquare \\ $$$${note}: \\ $$$${R}=\frac{{abc}}{\mathrm{4}{S}_{{A}\overset{\bigtriangleup} {{B}C}} },{sin}\frac{{A}}{\mathrm{2}}=\sqrt{\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{bc}}},{p}=\frac{{a}+{b}+{c}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 16/May/18
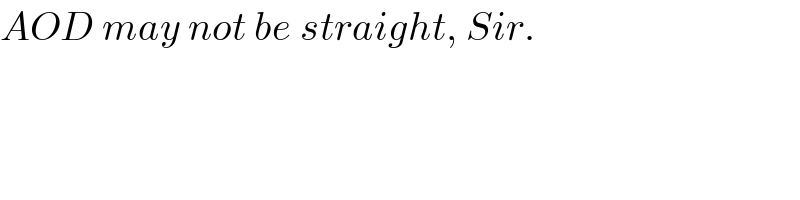
$${AOD}\:{may}\:{not}\:{be}\:{straight},\:{Sir}. \\ $$
