Question Number 35195 by ajfour last updated on 16/May/18

Commented by ajfour last updated on 16/May/18

$${Q}.\mathrm{35178}\:{carried}\:{forward}.. \\ $$
Answered by ajfour last updated on 18/May/18

$${lets}\:{take}\:{the}\:{common}\:{diameter} \\ $$$${as}\:{our}\:{y}\:{axis}.\:{L}\:{and}\:{T}\:{on}\:{x}\:{axis}. \\ $$$${further}\:{let}\:{AP}={l}\:,\:\:\angle{ALT}\:=\:\theta \\ $$$$\alpha=\frac{\angle{A}}{\mathrm{2}} \\ $$$${A}\left({l}\mathrm{cos}\:\theta,\:{r}+{l}\mathrm{sin}\:\theta\right)\:{is}\:{on}\:{circum}- \\ $$$${circle},\:{so} \\ $$$${l}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+\left({r}+{l}\mathrm{sin}\:\theta−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \:\:..\left(\boldsymbol{{i}}\right) \\ $$$${MR}={OP}\:\mathrm{cos}\:\left(\theta+\alpha−\frac{\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:{l}\mathrm{cos}\:\alpha−\frac{{b}}{\mathrm{2}}=\left({R}−{r}\right)\mathrm{sin}\:\left(\theta+\alpha\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left(\boldsymbol{{ii}}\right) \\ $$$${NS}={OP}\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\left(\theta−\alpha\right)\right) \\ $$$$\Rightarrow\:\:{l}\mathrm{cos}\:\alpha−\frac{{c}}{\mathrm{2}}=\left({R}−{r}\right)\mathrm{sin}\:\left(\theta−\alpha\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left(\boldsymbol{{iii}}\right) \\ $$$$\Rightarrow\:\mathrm{4}\left({R}−{r}\right)\mathrm{cos}\:\theta\mathrm{sin}\:\alpha=\:{c}−{b}\:\:\:…\left({a}\right) \\ $$$${and} \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3sin}\:^{\mathrm{2}} \theta\right)\mathrm{cos}\:^{\mathrm{2}} \alpha− \\ $$$$\:\:\:\:\:\:\left({R}−{r}\right)\left({b}+{c}\right)\mathrm{sin}\:\theta\mathrm{cos}\:\alpha+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\frac{{b}+{c}}{\mathrm{4}}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha\:=\:\mathrm{0}\:\:\:\:….\left({b}\right) \\ $$$${where}\:{R}=\frac{{a}}{\mathrm{2sin}\:\mathrm{2}\alpha}=\frac{{b}}{\mathrm{2sin}\:\mathrm{2}\beta}=\frac{{c}}{\mathrm{2sin}\:\mathrm{2}\gamma} \\ $$$$\:\:\:\alpha=\frac{\angle{A}}{\mathrm{2}}\:,\:\beta=\frac{\angle{B}}{\mathrm{2}}\:,\:\gamma=\frac{\angle{C}}{\mathrm{2}}\:. \\ $$$$\mathrm{sin}\:\theta,\:\mathrm{cos}\:\theta\:\:{need}\:{be}\:{eliminated}\:{amongst} \\ $$$${the}\:{equations}\:\left({a}\right),{and}\:\left({b}\right)! \\ $$
Commented by MJS last updated on 21/May/18

$$…\mathrm{this}\:\mathrm{is}\:\mathrm{possible}\:\mathrm{I}\:\mathrm{think}… \\ $$
Commented by ajfour last updated on 21/May/18
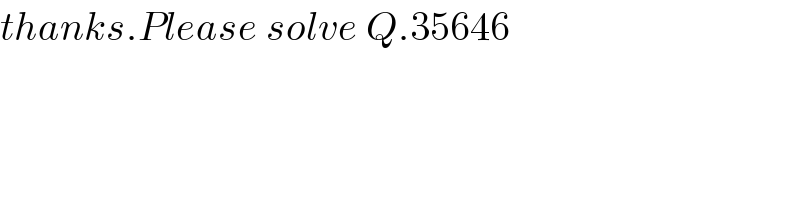
$${thanks}.{Please}\:{solve}\:{Q}.\mathrm{35646} \\ $$
Commented by MJS last updated on 22/May/18

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{work},\:\mathrm{Sir}\:\mathrm{Aifour},\:\mathrm{I}'\mathrm{m}\:\mathrm{glad} \\ $$$$\mathrm{to}\:\mathrm{add}\:\mathrm{my}\:\mathrm{part}: \\ $$$$\left({a}\right) \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta=\frac{{c}−{b}}{\mathrm{4}\left({R}−{r}\right)\mathrm{sin}\:\alpha};\:\mathrm{sin}\:\theta=\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\left({b}\right) \\ $$$$\Rightarrow\:{r}^{\mathrm{4}} +\mathcal{B}{r}^{\mathrm{3}} +\mathcal{C}{r}^{\mathrm{2}} +\mathcal{D}{r}+\mathcal{E}=\mathrm{0} \\ $$$$\mathrm{but}\:\mathrm{with}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{step}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{it}\:\mathrm{leads}\:\mathrm{to} \\ $$$${r}={s}−\frac{\mathcal{B}}{\mathrm{4}} \\ $$$${s}^{\mathrm{4}} +\mathcal{P}{s}^{\mathrm{2}} +\mathcal{Q}=\mathrm{0} \\ $$$${s}_{\mathrm{1}} =−\sqrt{−\frac{\mathcal{P}}{\mathrm{2}}−\frac{\sqrt{\mathcal{P}^{\mathrm{2}} −\mathrm{4}\mathcal{Q}}}{\mathrm{2}}} \\ $$$${s}_{\mathrm{2}} =−\sqrt{−\frac{\mathcal{P}}{\mathrm{2}}+\frac{\sqrt{\mathcal{P}^{\mathrm{2}} −\mathrm{4}\mathcal{Q}}}{\mathrm{2}}} \\ $$$${s}_{\mathrm{3}} =\sqrt{−\frac{\mathcal{P}}{\mathrm{2}}−\frac{\sqrt{\mathcal{P}^{\mathrm{2}} −\mathrm{4}\mathcal{Q}}}{\mathrm{2}}} \\ $$$${s}_{\mathrm{4}} =\sqrt{−\frac{\mathcal{P}}{\mathrm{2}}+\frac{\sqrt{\mathcal{P}^{\mathrm{2}} −\mathrm{4}\mathcal{Q}}}{\mathrm{2}}} \\ $$$${r}_{{i}} ={s}_{{i}} −\frac{\mathcal{B}}{\mathrm{4}} \\ $$$${R}=\frac{{abc}}{\delta};\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\alpha}{\mathrm{2}}};\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\alpha}{\mathrm{2}}}; \\ $$$$\mathrm{cos}\:\alpha=\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{bc}};\:\delta=\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}−{b}+{c}\right)\left(−{a}+{b}+{c}\right)} \\ $$$$\mathcal{B}=−\frac{\mathrm{4}{abc}}{\delta}=−\mathrm{4}{R} \\ $$$$\mathcal{P}=\frac{{bc}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} \left({b}^{\mathrm{2}} +\mathrm{6}{bc}+{c}^{\mathrm{2}} \right)+\delta^{\mathrm{2}} \right)}{\mathrm{4}\delta^{\mathrm{2}} } \\ $$$$\mathcal{Q}=\frac{{a}^{\mathrm{2}} {b}^{\mathrm{3}} {c}^{\mathrm{3}} \left({b}−{c}\right)^{\mathrm{2}} \left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)}{\mathrm{4}\delta^{\mathrm{2}} } \\ $$$$\frac{\sqrt{\mathcal{P}^{\mathrm{2}} −\mathrm{4}\mathcal{Q}}}{\mathrm{2}}=\frac{{bc}\left({b}+{c}\right)^{\mathrm{2}} }{\mathrm{8}\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)} \\ $$$$\sqrt{−\frac{\mathcal{P}}{\mathrm{2}}−\frac{\sqrt{\mathcal{P}^{\mathrm{2}} −\mathrm{4}\mathcal{Q}}}{\mathrm{2}}}=\frac{\left({b}−{c}\right)\sqrt{{bc}}}{\mathrm{2}\sqrt{\left({a}+{b}−{c}\right)\left({a}−{b}+{c}\right)}} \\ $$$$\sqrt{−\frac{\mathcal{P}}{\mathrm{2}}+\frac{\sqrt{\mathcal{P}^{\mathrm{2}} −\mathrm{4}\mathcal{Q}}}{\mathrm{2}}}=\frac{{abc}}{\delta}={R} \\ $$$${r}_{\mathrm{1}} ={R}−\frac{\left({b}−{c}\right)\sqrt{{bc}}}{\mathrm{2}\sqrt{\left({a}+{b}−{c}\right)\left({a}−{b}+{c}\right)}} \\ $$$${r}_{\mathrm{2}} ={R}−{R}=\mathrm{0} \\ $$$${r}_{\mathrm{3}} ={R}+\frac{\left({b}−{c}\right)\sqrt{{bc}}}{\mathrm{2}\sqrt{\left({a}+{b}−{c}\right)\left({a}−{b}+{c}\right)}} \\ $$$${r}_{\mathrm{4}} ={R}+{R}=\mathrm{2}{R} \\ $$$$ \\ $$$${r}_{\mathrm{1}} \:\mathrm{and}\:{r}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{same}\:\mathrm{if}\:\mathrm{we}\:\mathrm{interchange} \\ $$$${b}\:\mathrm{and}\:{c}.\:\mathrm{Could}\:\mathrm{the}\:\mathrm{lower}\:\mathrm{value}\:\mathrm{be}\:\mathrm{the}\:\mathrm{radius} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{touching}\:\mathrm{the}\:\mathrm{circumcircle}\:\mathrm{inside} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{higher}\:\mathrm{value}\:\mathrm{be}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{circle}\:\mathrm{touching}\:\mathrm{it}\:\mathrm{from}\:\mathrm{outside}? \\ $$$${r}_{\mathrm{2}} =\mathrm{0}\:\mathrm{is}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{identical} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{point}\:{A}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}. \\ $$$$\mathrm{But}\:\mathrm{what}\:\mathrm{about}\:{r}_{\mathrm{4}} =\mathrm{2}{R}? \\ $$$$\mathrm{Please}\:\mathrm{try}\:\mathrm{to}\:\mathrm{construct}\:\mathrm{all}\:\mathrm{of}\:\mathrm{them}\:\mathrm{for}\:\mathrm{a} \\ $$$$\mathrm{given}\:\mathrm{triangle},\:\mathrm{using}\:\mathrm{my}\:\mathrm{formulas}.\:\mathrm{I}'\mathrm{m} \\ $$$$\mathrm{afraid}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{the}\:\mathrm{time}\:\mathrm{to}\:\mathrm{do}\:\mathrm{it}\:\mathrm{myself}, \\ $$$$\mathrm{and}\:\mathrm{let}\:\mathrm{me}\:\mathrm{know}\:\mathrm{if}\:\mathrm{we}\:\mathrm{made}\:\mathrm{any}\:\mathrm{mistake}… \\ $$$$ \\ $$$$…\mathrm{it}'\mathrm{s}\:\mathrm{wrong}\:\mathrm{for}\:\mathrm{an}\:\mathrm{equilateral}\:\mathrm{triangle}… \\ $$$$…\mathrm{it}'\mathrm{s}\:\mathrm{wrong}\:\mathrm{for}\:{b}={c}… \\ $$
Commented by ajfour last updated on 22/May/18

$${Thanks}\:{for}\:{the}\:{effort},\:{let}\:{me} \\ $$$${comprehend}\:{it}\:{all},\:{surely}\:{its} \\ $$$${gonna}\:{take}\:{a}\:{while}\:! \\ $$
