Question-35258

Question Number 35258 by Tinkutara last updated on 17/May/18

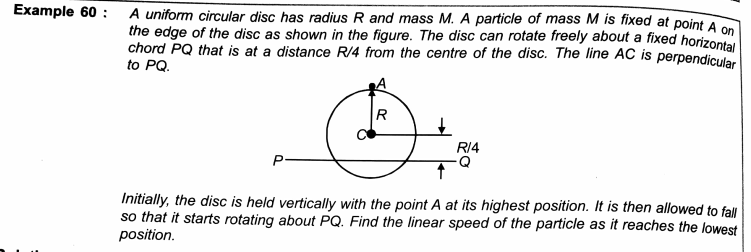
Answered by ajfour last updated on 17/May/18

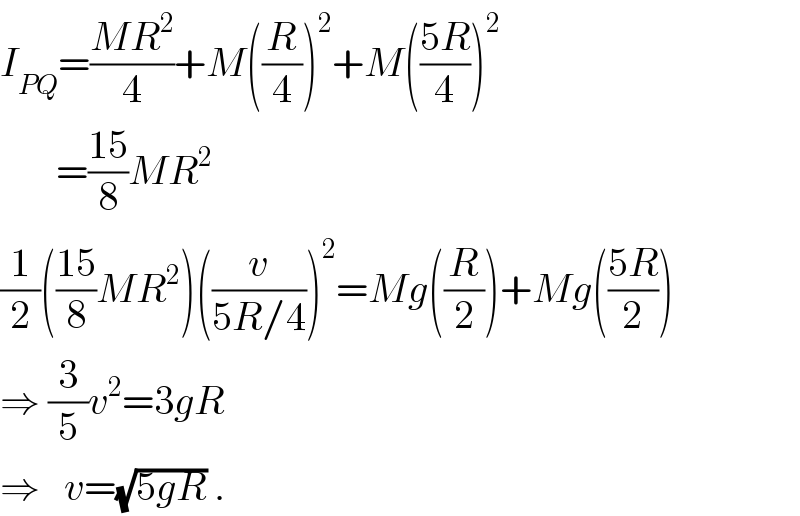
I_(PQ) =((MR^2 )/4)+M((R/4))^2 +M(((5R)/4))^2 =((15)/8)MR^2 (1/2)(((15)/8)MR^2 )((v/(5R/4)))^2 =Mg((R/2))+Mg(((5R)/2)) ⇒ (3/5)v^2 =3gR ⇒ v=(√(5gR)) .

$${I}_{{PQ}} =\frac{{MR}^{\mathrm{2}} }{\mathrm{4}}+{M}\left(\frac{{R}}{\mathrm{4}}\right)^{\mathrm{2}} +{M}\left(\frac{\mathrm{5}{R}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{15}}{\mathrm{8}}{MR}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{15}}{\mathrm{8}}{MR}^{\mathrm{2}} \right)\left(\frac{{v}}{\mathrm{5}{R}/\mathrm{4}}\right)^{\mathrm{2}} ={Mg}\left(\frac{{R}}{\mathrm{2}}\right)+{Mg}\left(\frac{\mathrm{5}{R}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\frac{\mathrm{3}}{\mathrm{5}}{v}^{\mathrm{2}} =\mathrm{3}{gR} \\ $$$$\Rightarrow\:\:\:{v}=\sqrt{\mathrm{5}{gR}}\:. \\ $$

Commented by Tinkutara last updated on 17/May/18

Sir please explain line 3.

Commented by ajfour last updated on 17/May/18

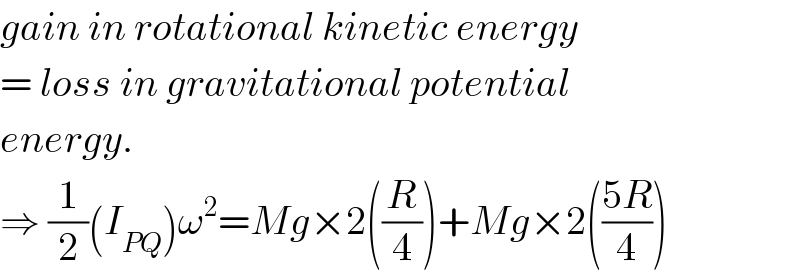
gain in rotational kinetic energy = loss in gravitational potential energy. ⇒ (1/2)(I_(PQ) )ω^2 =Mg×2((R/4))+Mg×2(((5R)/4))

$${gain}\:{in}\:{rotational}\:{kinetic}\:{energy} \\ $$$$=\:{loss}\:{in}\:{gravitational}\:{potential} \\ $$$${energy}. \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\left({I}_{{PQ}} \right)\omega^{\mathrm{2}} ={Mg}×\mathrm{2}\left(\frac{{R}}{\mathrm{4}}\right)+{Mg}×\mathrm{2}\left(\frac{\mathrm{5}{R}}{\mathrm{4}}\right) \\ $$

Commented by Tinkutara last updated on 17/May/18

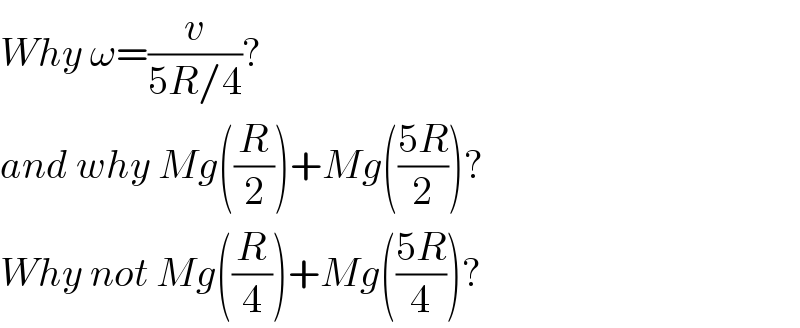
Why ω=(v/(5R/4))? and why Mg((R/2))+Mg(((5R)/2))? Why not Mg((R/4))+Mg(((5R)/4))?

$${Why}\:\omega=\frac{{v}}{\mathrm{5}{R}/\mathrm{4}}? \\ $$$${and}\:{why}\:{Mg}\left(\frac{{R}}{\mathrm{2}}\right)+{Mg}\left(\frac{\mathrm{5}{R}}{\mathrm{2}}\right)? \\ $$$${Why}\:{not}\:{Mg}\left(\frac{{R}}{\mathrm{4}}\right)+{Mg}\left(\frac{\mathrm{5}{R}}{\mathrm{4}}\right)? \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply