Question Number 35267 by Tinkutara last updated on 17/May/18

Answered by ajfour last updated on 17/May/18

$${q}=\left(\pi{r}_{\mathrm{0}} ^{\mathrm{2}} \right){v}_{\mathrm{0}} =\left(\pi{r}^{\mathrm{2}} \right){v} \\ $$$${v}^{\mathrm{2}} ={v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}{gh} \\ $$$$\Rightarrow\:{v}_{\mathrm{0}} ^{\mathrm{2}} \left(\frac{{r}_{\mathrm{0}} }{{r}}\right)^{\mathrm{4}} ={v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}{gh} \\ $$$$\Rightarrow\:{r}\:=\:{r}_{\mathrm{0}} \left(\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{{v}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}{gh}}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{4}×\mathrm{10}^{−\mathrm{3}} \left(\frac{\mathrm{0}.\mathrm{16}}{\mathrm{0}.\mathrm{16}+\mathrm{4}}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:{d}=\mathrm{2}{r}\:=\:\mathrm{8}×\mathrm{10}^{−\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{26}}\right)^{\mathrm{1}/\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{8}}{\mathrm{2}.\mathrm{24}}×\mathrm{10}^{−\mathrm{3}} \approx\:\frac{\mathrm{32}}{\mathrm{9}}×\mathrm{10}^{−\mathrm{3}} \\ $$$${hence}\:\:\left({c}\right)\:. \\ $$
Commented by Tinkutara last updated on 17/May/18

$${Why}\:{can}'{t}\:{we}\:{use} \\ $$$$\rho{gh}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}\rho{v}_{\mathrm{1}} ^{\mathrm{2}} =\rho{gh}_{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\rho{v}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$? \\ $$
Commented by ajfour last updated on 17/May/18

$${yes}\:{we}\:{can}. \\ $$
Commented by Tinkutara last updated on 17/May/18
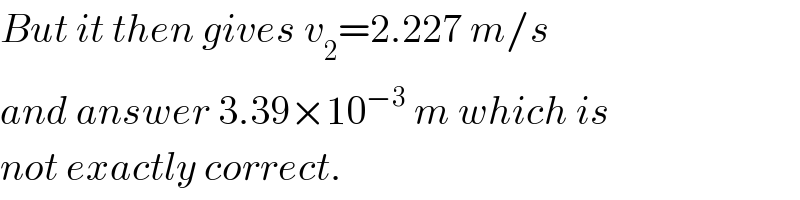
$${But}\:{it}\:{then}\:{gives}\:{v}_{\mathrm{2}} =\mathrm{2}.\mathrm{227}\:{m}/{s} \\ $$$${and}\:{answer}\:\mathrm{3}.\mathrm{39}×\mathrm{10}^{−\mathrm{3}} \:{m}\:{which}\:{is} \\ $$$${not}\:{exactly}\:{correct}. \\ $$
