Question Number 35279 by ajfour last updated on 17/May/18
Commented by ajfour last updated on 17/May/18

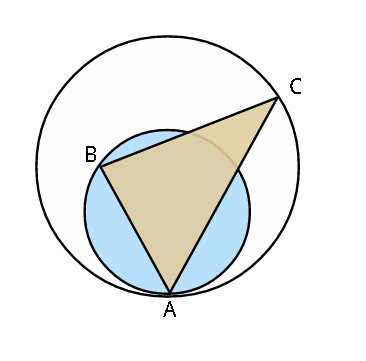
$${Given}\:{two}\:{circles}\:{of}\:{radii}\:\boldsymbol{{r}}\:{and}\:\boldsymbol{{R}}. \\ $$$${The}\:{circles}\:{touch}\:{each}\:{other} \\ $$$${internally}.\:{Triangle}\:{ABC}\:{has} \\ $$$${its}\:{vertex}\:\boldsymbol{{A}}\:{at}\:{the}\:{point}\:{where} \\ $$$${the}\:{circles}\:{touch}.\:{Vertex}\:\boldsymbol{{B}}\:{lies} \\ $$$${on}\:{the}\:{circumference}\:{of}\:{smaller} \\ $$$${circle}\:{of}\:{radius}\:\boldsymbol{{r}}\:{while}\:{vertex}\:\boldsymbol{{C}} \\ $$$${lies}\:{on}\:{circumference}\:{of}\:{circle} \\ $$$${of}\:{radius}\:\boldsymbol{{R}}. \\ $$$${Find}\:{maximum}\:{area}\:{of}\:\bigtriangleup{ABC} \\ $$$${in}\:{terms}\:{of}\:\boldsymbol{{r}},\:{and}\:\boldsymbol{{R}}. \\ $$
Commented by ajfour last updated on 17/May/18
Commented by ajfour last updated on 17/May/18
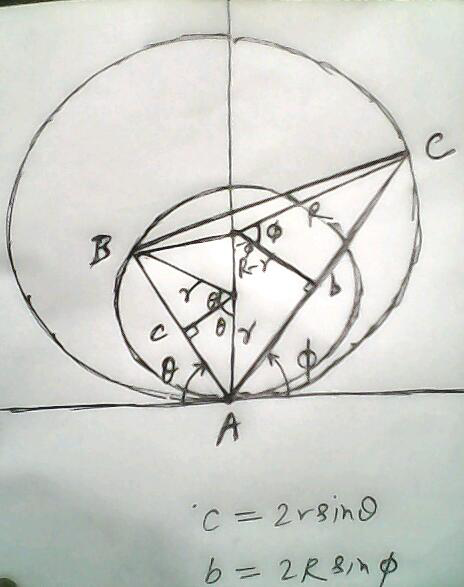
![A(θ,φ)=(1/2)bcsin (θ+φ) b=2Rsin φ , c=2rsin θ A(θ,φ)=2rRsin θsin φsin (θ+φ) (∂A/∂θ)=2rRsin φ[cos θsin (θ+φ) +sin θcos (θ+φ)]=0 ⇒ sin φ=0,π or sin (2θ+φ)=0 similarly (∂A/∂φ)=0 ⇒ sin θ=0,π or sin (2φ+θ)=0 for our case ⇒ 2θ+φ=π and 2φ+θ=π ⇒ θ+φ=((2π)/3) So θ=φ=(π/3) A=(2rR)(((3(√3))/8)) =((3(√3)rR)/4) .](https://www.tinkutara.com/question/Q35287.png)
$${A}\left(\theta,\phi\right)=\frac{\mathrm{1}}{\mathrm{2}}{bc}\mathrm{sin}\:\left(\theta+\phi\right) \\ $$$${b}=\mathrm{2}{R}\mathrm{sin}\:\phi\:\:,\:\:{c}=\mathrm{2}{r}\mathrm{sin}\:\theta \\ $$$${A}\left(\theta,\phi\right)=\mathrm{2}{rR}\mathrm{sin}\:\theta\mathrm{sin}\:\phi\mathrm{sin}\:\left(\theta+\phi\right) \\ $$$$\frac{\partial{A}}{\partial\theta}=\mathrm{2}{rR}\mathrm{sin}\:\phi\left[\mathrm{cos}\:\theta\mathrm{sin}\:\left(\theta+\phi\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{sin}\:\theta\mathrm{cos}\:\left(\theta+\phi\right)\right]=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{sin}\:\phi=\mathrm{0},\pi\:\:{or} \\ $$$$\:\:\:\:\:\:\:\mathrm{sin}\:\left(\mathrm{2}\theta+\phi\right)=\mathrm{0} \\ $$$${similarly}\:\:\frac{\partial{A}}{\partial\phi}=\mathrm{0}\:\Rightarrow\:\:\:\mathrm{sin}\:\theta=\mathrm{0},\pi \\ $$$${or}\:\:\:\mathrm{sin}\:\left(\mathrm{2}\phi+\theta\right)=\mathrm{0} \\ $$$${for}\:{our}\:{case} \\ $$$$\Rightarrow\:\:\mathrm{2}\theta+\phi=\pi\:\:{and}\:\:\mathrm{2}\phi+\theta=\pi \\ $$$$\Rightarrow\:\:\theta+\phi=\frac{\mathrm{2}\pi}{\mathrm{3}}\: \\ $$$${So}\:\:\theta=\phi=\frac{\pi}{\mathrm{3}} \\ $$$${A}=\left(\mathrm{2}{rR}\right)\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)\:=\frac{\mathrm{3}\sqrt{\mathrm{3}}\boldsymbol{{rR}}}{\mathrm{4}}\:. \\ $$
