Question Number 35294 by ajfour last updated on 17/May/18
Commented by ajfour last updated on 17/May/18

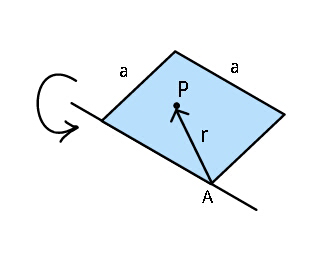
$${Find}\:{moment}\:{of}\:{inertia}\:{of}\:{a} \\ $$$${square}\:{plate}\:{if}\:{its}\:{density}\:{at}\:{a} \\ $$$${point}\:\left({say}\:{P}\right)\:{is}\:{proportional}\:{to}\:{the} \\ $$$${distance}\:{of}\:{that}\:{point}\:{from} \\ $$$${vertex}\:{A}. \\ $$
Answered by ajfour last updated on 18/May/18
![lets take the rotational axis the y axis. A the origin. dI=ρx^2 (dy)(dx) let ρ=kr ⇒ I = k ∫_0 ^( a) [∫_0 ^( a) x^2 (√(x^2 +y^2 )) dy]dx or let x=rcos θ , y=rsin θ I=∫_0 ^( π/4) [∫_0 ^( asec θ) kr(r^2 cos^2 θ)(rdr)]dθ +∫_(π/4) ^( π/2) [∫_0 ^( acosec θ) kr(r^2 cos^2 θ)rdr]dθ =((ka^5 )/5)[∫_0 ^( π/4) sec^3 θdθ+∫_(π/4) ^( π/2) cot^2 θcosec^3 θdθ] =((ka^5 )/5)(I_1 +I_2 ) I_1 =∫_0 ^( π/4) sec θsec^2 θdθ =sec θtan θ∣_0 ^(π/4) −∫_0 ^( π/4) (sec^2 θ−1)sec θdθ ⇒ 2I_1 =(√2)+ln ∣sec θ+tan θ∣_0 ^(π/4) ⇒ I_1 =((√2)/2)+(1/2)ln (1+(√2)) I_2 = ∫_(π/4) ^( π/2) cot^2 θcosec^3 θdθ let φ=(π/2)−θ ⇒ dφ=−dθ I_2 =∫_0 ^( π/4) tan^2 θsec^3 θdθ let tan θ=t ⇒ dt=sec^2 θdθ =∫_0 ^( 1) t^2 (√(1+t^2 )) dt =(t^3 /3)(√(1+t^2 )) ∣_0 ^1 −∫_0 ^( 1) (t^3 /3)×(t/( (√(1+t^2 ))))dt 3I_2 =(√2)−∫_0 ^( 1) ((t^4 −1)/( (√(1+t^2 ))))dt−∫_0 ^( 1) (dt/( (√(1+t^2 )))) 3I_2 = (√2)−∫_0 ^( 1) (t^2 −1)(√(1+t^2 )) dt−∫(dt/( (√(1+t^2 )))) 4I_2 = (√2)+∫_0 ^( 1) (√(1+t^2 ))−∫_0 ^( 1) (dt/( (√(1+t^2 )))) = (√2)+((t/2)(√(1+t^2 )))∣_0 ^1 +(1/2)ln ∣t+(√(1+t^2 ))∣_0 ^1 −ln ∣t+(√(1+t^2 ))∣_0 ^1 ⇒ I_2 =((√2)/4)+((√2)/8)−(1/8)ln (1+(√2)) As I=((ka^5 )/5)(I_1 +I_2 ) I=((ka^5 )/5)[((√2)/2)+(1/2)ln (1+(√2))+ +((√2)/4)+((√2)/8)−(1/8)ln (1+(√2))] ⇒ I = ((ka^5 )/(40))[7(√2)+3ln (1+(√2)] .](https://www.tinkutara.com/question/Q35301.png)
$${lets}\:{take}\:{the}\:{rotational}\:{axis}\:{the} \\ $$$${y}\:{axis}.\:{A}\:{the}\:{origin}. \\ $$$${dI}=\rho{x}^{\mathrm{2}} \left({dy}\right)\left({dx}\right) \\ $$$${let}\:\:\rho={kr} \\ $$$$\Rightarrow\:\:{I}\:=\:{k}\:\int_{\mathrm{0}} ^{\:\:{a}} \left[\int_{\mathrm{0}} ^{\:\:{a}} {x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:{dy}\right]{dx} \\ $$$$\:\:\:{or} \\ $$$${let}\:{x}={r}\mathrm{cos}\:\theta\:\:,\:\:{y}={r}\mathrm{sin}\:\theta \\ $$$${I}=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left[\int_{\mathrm{0}} ^{\:\:{a}\mathrm{sec}\:\theta} {kr}\left({r}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)\left({rdr}\right)\right]{d}\theta \\ $$$$\:+\int_{\pi/\mathrm{4}} ^{\:\:\pi/\mathrm{2}} \left[\int_{\mathrm{0}} ^{\:\:{a}\mathrm{cosec}\:\theta} {kr}\left({r}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right){rdr}\right]{d}\theta \\ $$$$=\frac{{ka}^{\mathrm{5}} }{\mathrm{5}}\left[\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \mathrm{sec}\:^{\mathrm{3}} \theta{d}\theta+\int_{\pi/\mathrm{4}} ^{\:\:\pi/\mathrm{2}} \mathrm{cot}\:^{\mathrm{2}} \theta\mathrm{cosec}\:^{\mathrm{3}} \theta{d}\theta\right] \\ $$$$=\frac{{ka}^{\mathrm{5}} }{\mathrm{5}}\left({I}_{\mathrm{1}} +{I}_{\mathrm{2}} \right) \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \mathrm{sec}\:\theta\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\:\:=\mathrm{sec}\:\theta\mathrm{tan}\:\theta\mid_{\mathrm{0}} ^{\pi/\mathrm{4}} −\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{sec}\:^{\mathrm{2}} \theta−\mathrm{1}\right)\mathrm{sec}\:\theta{d}\theta \\ $$$$\Rightarrow\:\mathrm{2}{I}_{\mathrm{1}} =\sqrt{\mathrm{2}}+\mathrm{ln}\:\mid\mathrm{sec}\:\theta+\mathrm{tan}\:\theta\mid_{\mathrm{0}} ^{\pi/\mathrm{4}} \\ $$$$\Rightarrow\:{I}_{\mathrm{1}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$${I}_{\mathrm{2}} =\:\int_{\pi/\mathrm{4}} ^{\:\:\pi/\mathrm{2}} \mathrm{cot}\:^{\mathrm{2}} \theta\mathrm{cosec}\:^{\mathrm{3}} \theta{d}\theta \\ $$$${let}\:\phi=\frac{\pi}{\mathrm{2}}−\theta\:\:\:\Rightarrow\:\:{d}\phi=−{d}\theta \\ $$$$\:\:{I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \mathrm{tan}\:^{\mathrm{2}} \theta\mathrm{sec}\:^{\mathrm{3}} \theta{d}\theta \\ $$$${let}\:\:\mathrm{tan}\:\theta={t}\:\:\:\Rightarrow\:\:{dt}=\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} {t}^{\mathrm{2}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$\:\:\:\:\:=\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\mid_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{t}^{\mathrm{3}} }{\mathrm{3}}×\frac{{t}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{dt} \\ $$$$\:\:\mathrm{3}{I}_{\mathrm{2}} =\sqrt{\mathrm{2}}−\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{t}^{\mathrm{4}} −\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{dt}−\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$\mathrm{3}{I}_{\mathrm{2}} =\:\sqrt{\mathrm{2}}−\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}−\int\frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$\mathrm{4}{I}_{\mathrm{2}} =\:\sqrt{\mathrm{2}}+\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }−\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:=\:\sqrt{\mathrm{2}}+\left(\frac{{t}}{\mathrm{2}}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\mid_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{ln}\:\mid{t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Rightarrow\:{I}_{\mathrm{2}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$${As}\:\:\:\:\:{I}=\frac{{ka}^{\mathrm{5}} }{\mathrm{5}}\left({I}_{\mathrm{1}} +{I}_{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:{I}=\frac{\boldsymbol{{ka}}^{\mathrm{5}} }{\mathrm{5}}\left[\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right] \\ $$$$\:\Rightarrow\:\:\boldsymbol{{I}}\:=\:\frac{\boldsymbol{{ka}}^{\mathrm{5}} }{\mathrm{40}}\left[\mathrm{7}\sqrt{\mathrm{2}}+\mathrm{3ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right]\:.\right. \\ $$
