Question Number 35362 by 26488679 last updated on 18/May/18

Commented by 26488679 last updated on 18/May/18
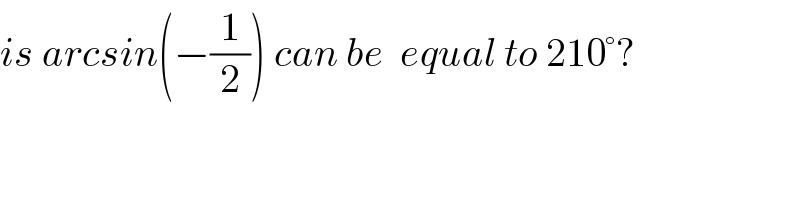
$${is}\:{arcsin}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\:{can}\:{be}\:\:{equal}\:{to}\:\mathrm{210}°? \\ $$
Commented by ajfour last updated on 18/May/18

$${not}\:{a}\:{principal}\:{value}. \\ $$
Commented by prof Abdo imad last updated on 18/May/18
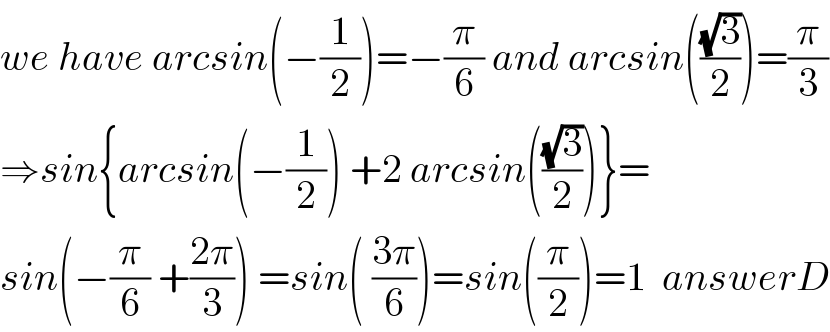
$${we}\:{have}\:{arcsin}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\pi}{\mathrm{6}}\:{and}\:{arcsin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow{sin}\left\{{arcsin}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\:+\mathrm{2}\:{arcsin}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right\}= \\ $$$${sin}\left(−\frac{\pi}{\mathrm{6}}\:+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\:={sin}\left(\:\frac{\mathrm{3}\pi}{\mathrm{6}}\right)={sin}\left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{1}\:\:{answerD} \\ $$
Answered by ajfour last updated on 18/May/18
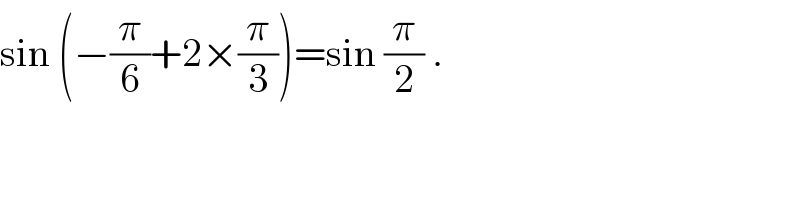
$$\mathrm{sin}\:\left(−\frac{\pi}{\mathrm{6}}+\mathrm{2}×\frac{\pi}{\mathrm{3}}\right)=\mathrm{sin}\:\frac{\pi}{\mathrm{2}}\:. \\ $$
