Menu Close

Question-35390

Tinku Tara 0 Comments
Pin




Question Number 35390 by ajfour last updated on 18/May/18
Commented by ajfour last updated on 18/May/18
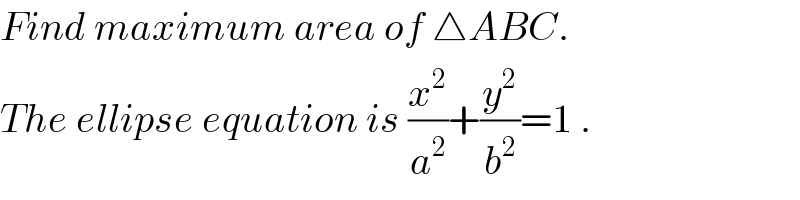
Find maximum area of △ABC. The ellipse equation is (x^2 /a^2 )+(y^2 /b^2 )=1 .
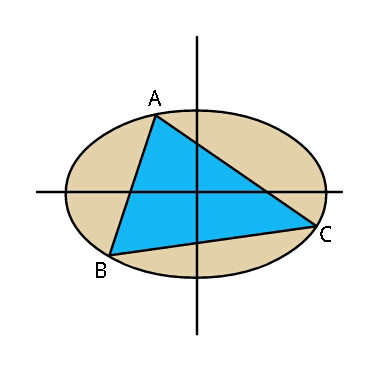
$${Find}\:{maximum}\:{area}\:{of}\:\bigtriangleup{ABC}. \\ $$$${The}\:{ellipse}\:{equation}\:{is}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:. \\ $$
Commented by MJS last updated on 18/May/18
lol. I solved this some years ago, not knowing that Steiner solved it long before me. all triangles with barycenter in the center of the ellipse are of equal area. I will post my proof but it might take some time. google Steiner−ellipse or look it up on Wikipedia
$$\mathrm{lol}.\:\mathrm{I}\:\mathrm{solved}\:\mathrm{this}\:\mathrm{some}\:\mathrm{years}\:\mathrm{ago},\:\mathrm{not}\:\mathrm{knowing} \\ $$$$\mathrm{that}\:\mathrm{Steiner}\:\mathrm{solved}\:\mathrm{it}\:\mathrm{long}\:\mathrm{before}\:\mathrm{me}. \\ $$$$\mathrm{all}\:\mathrm{triangles}\:\mathrm{with}\:\mathrm{barycenter}\:\mathrm{in}\:\mathrm{the}\:\mathrm{center} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{ellipse}\:\mathrm{are}\:\mathrm{of}\:\mathrm{equal}\:\mathrm{area}. \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{post}\:\mathrm{my}\:\mathrm{proof}\:\mathrm{but}\:\mathrm{it}\:\mathrm{might}\:\mathrm{take}\:\mathrm{some} \\ $$$$\mathrm{time}. \\ $$$$\mathrm{google}\:{Steiner}−{ellipse}\:\mathrm{or}\:\mathrm{look}\:\mathrm{it}\:\mathrm{up}\:\mathrm{on}\: \\ $$$${Wikipedia} \\ $$
Commented by MJS last updated on 18/May/18
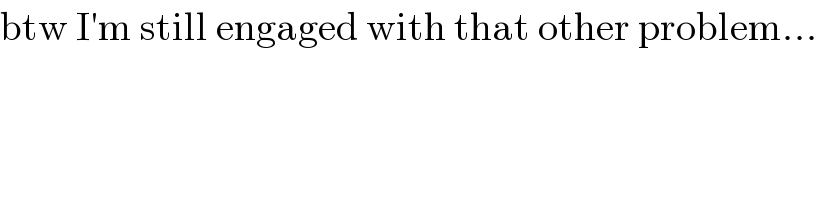
btw I′m still engaged with that other problem...
$$\mathrm{btw}\:\mathrm{I}'\mathrm{m}\:\mathrm{still}\:\mathrm{engaged}\:\mathrm{with}\:\mathrm{that}\:\mathrm{other}\:\mathrm{problem}… \\ $$
Commented by ajfour last updated on 18/May/18
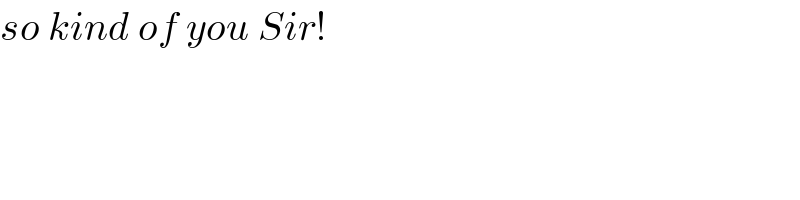
so kind of you Sir!
$${so}\:{kind}\:{of}\:{you}\:{Sir}! \\ $$
Commented by MJS last updated on 18/May/18
start with a circle with radius a x^2 +(y^∗ )^2 =a^2 insert an equilateral triangle A^∗ B^∗ C^∗ with A^∗ = ((x_A ),((y_A ^∗ =(a/b)y_A )) ) ; B^∗ = ((x_B ),((y_B ^∗ =(a/b)y_B )) ) ;C^∗ = ((x_C ),((y_C ^∗ =(a/b)y_C )) ) now transform y=(b/a)y^∗ the circle becomes the ellipse with area_(ell) =(b/a)×area_(circle) =abπ the equilateral triangle becomes the given one with area_△ =(b/a)×area_(equi△) it should be easy to see that the barycenter stays in place and all possible triangles have the same area. I will post some equations for calculating both directions: find smallest ellipse to a given triangle and find the angle and ratio to transform a equilateral triangle into any triangle... just give me some time to find these formulas within the chaos in my library...
$$\mathrm{start}\:\mathrm{with}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{radius}\:{a} \\ $$$${x}^{\mathrm{2}} +\left({y}^{\ast} \right)^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\mathrm{insert}\:\mathrm{an}\:\mathrm{equilateral}\:\mathrm{triangle}\:{A}^{\ast} {B}^{\ast} {C}^{\ast} \:\mathrm{with} \\ $$$${A}^{\ast} =\begin{pmatrix}{{x}_{{A}} }\\{{y}_{{A}} ^{\ast} =\frac{{a}}{{b}}{y}_{{A}} }\end{pmatrix}\:;\:{B}^{\ast} =\begin{pmatrix}{{x}_{{B}} }\\{{y}_{{B}} ^{\ast} =\frac{{a}}{{b}}{y}_{{B}} }\end{pmatrix}\:;{C}^{\ast} =\begin{pmatrix}{{x}_{{C}} }\\{{y}_{{C}} ^{\ast} =\frac{{a}}{{b}}{y}_{{C}} }\end{pmatrix} \\ $$$$\mathrm{now}\:\mathrm{transform}\:{y}=\frac{{b}}{{a}}{y}^{\ast} \\ $$$$\mathrm{the}\:\mathrm{circle}\:\mathrm{becomes}\:\mathrm{the}\:\mathrm{ellipse} \\ $$$$\:\:\:\:\:\mathrm{with}\:\mathrm{area}_{\mathrm{ell}} =\frac{{b}}{{a}}×\mathrm{area}_{\mathrm{circle}} ={ab}\pi \\ $$$$\mathrm{the}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{becomes}\:\mathrm{the}\:\mathrm{given}\:\mathrm{one} \\ $$$$\:\:\:\:\:\mathrm{with}\:\mathrm{area}_{\bigtriangleup} =\frac{{b}}{{a}}×\mathrm{area}_{\mathrm{equi}\bigtriangleup} \\ $$$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{the}\:\mathrm{barycenter} \\ $$$$\mathrm{stays}\:\mathrm{in}\:\mathrm{place}\:\mathrm{and}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{triangles} \\ $$$$\mathrm{have}\:\mathrm{the}\:\mathrm{same}\:\mathrm{area}. \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{post}\:\mathrm{some}\:\mathrm{equations}\:\mathrm{for}\:\mathrm{calculating} \\ $$$$\mathrm{both}\:\mathrm{directions}:\:\mathrm{find}\:\mathrm{smallest}\:\mathrm{ellipse}\:\mathrm{to}\:\mathrm{a} \\ $$$$\mathrm{given}\:\mathrm{triangle}\:\mathrm{and}\:\mathrm{find}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{and}\:\mathrm{ratio} \\ $$$$\mathrm{to}\:\mathrm{transform}\:\mathrm{a}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{into} \\ $$$$\mathrm{any}\:\mathrm{triangle}…\:\mathrm{just}\:\mathrm{give}\:\mathrm{me}\:\mathrm{some}\:\mathrm{time}\:\mathrm{to} \\ $$$$\mathrm{find}\:\mathrm{these}\:\mathrm{formulas}\:\mathrm{within}\:\mathrm{the}\:\mathrm{chaos}\:\mathrm{in}\:\mathrm{my} \\ $$$$\mathrm{library}… \\ $$
Commented by ajfour last updated on 18/May/18
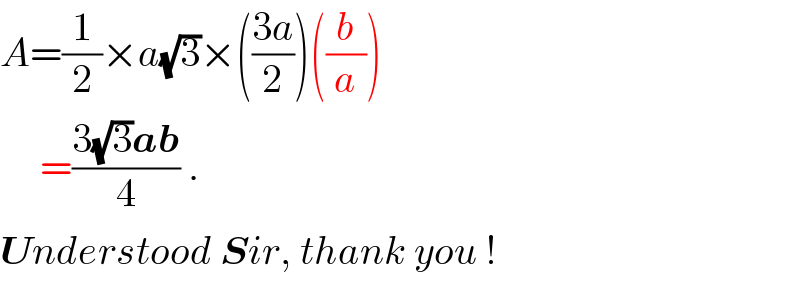
A=(1/2)×a(√3)×(((3a)/2))((b/a)) =((3(√3)ab)/4) . Understood Sir, thank you !
$${A}=\frac{\mathrm{1}}{\mathrm{2}}×{a}\sqrt{\mathrm{3}}×\left(\frac{\mathrm{3}{a}}{\mathrm{2}}\right)\left(\frac{{b}}{{a}}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{3}\sqrt{\mathrm{3}}\boldsymbol{{ab}}}{\mathrm{4}}\:. \\ $$$$\boldsymbol{{U}}{nderstood}\:\boldsymbol{{S}}{ir},\:{thank}\:{you}\:! \\ $$
Answered by rahul 19 last updated on 18/May/18
((3(√3))/4) ab .
$$\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{4}}\:{ab}\:. \\ $$
Commented by rahul 19 last updated on 19/May/18
Got the same answer by assuming triangle to be isosceles !:)
$$\:{Got}\:{the}\:{same}\:{answer}\:{by}\:{assuming} \\ $$$$\left.{triangle}\:{to}\:{be}\:{isosceles}\:!:\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *