Question Number 35430 by ajfour last updated on 18/May/18

Commented by ajfour last updated on 19/May/18
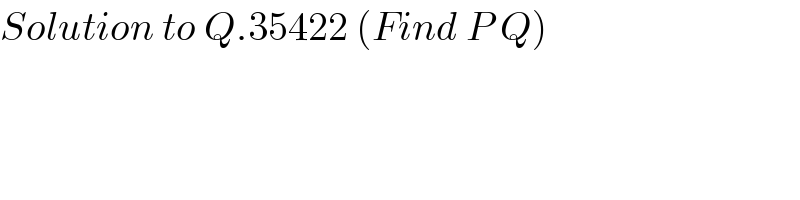
$${Solution}\:{to}\:{Q}.\mathrm{35422}\:\left({Find}\:{P}\:{Q}\right) \\ $$
Answered by ajfour last updated on 20/May/18
![We shall orient the xyz coordinate system as shown with A as origin. So line APQ lies entirely in xz plane. eqn. of sphere: (x−acos φ)^2 +(y−asin φ)^2 +(z−R)^2 =R^2 eqn. of circle of intersection of sphere with xz plane (y=0) is (x−acos φ)^2 +(z−R)^2 =R^2 −a^2 sin^2 φ equation of APQ is z=xtan θ For x coordinates of P and Q (intersection of circle with line) (x−acos φ)^2 +(xtan θ−R)^2 =R^2 −a^2 sin^2 φ x^2 sec^2 θ−2x(scos φ+Rtan θ)+a^2 =0 PQ=∣x_Q −x_P ∣sec θ ∣x_Q −x_P ∣=(√((x_Q +x_P )^2 −4x_B x_P )) ⇒ PQ=(sec θ)(√([((2(acos φ+Rtan θ))/(sec^2 θ))]^2 −((4a^2 )/(sec^2 θ)))) P Q=2(√((acos φ+Rtan θ)^2 cos^2 θ−a^2 )) .](https://www.tinkutara.com/question/Q35432.png)
$${We}\:{shall}\:{orient}\:{the}\:{xyz}\:{coordinate} \\ $$$${system}\:{as}\:{shown}\:{with}\:{A}\:{as}\:{origin}. \\ $$$${So}\:{line}\:{APQ}\:{lies}\:{entirely}\:{in}\: \\ $$$${xz}\:{plane}. \\ $$$${eqn}.\:{of}\:{sphere}: \\ $$$$\left({x}−{a}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +\left({y}−{a}\mathrm{sin}\:\phi\right)^{\mathrm{2}} +\left({z}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${eqn}.\:{of}\:{circle}\:{of}\:{intersection}\:{of} \\ $$$${sphere}\:{with}\:{xz}\:{plane}\:\left({y}=\mathrm{0}\right)\:{is} \\ $$$$\left({x}−{a}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +\left({z}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} −{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi \\ $$$${equation}\:{of}\:{APQ}\:{is} \\ $$$$\:\:\:\:\:\:\:\:{z}={x}\mathrm{tan}\:\theta \\ $$$${For}\:{x}\:{coordinates}\:{of}\:{P}\:{and}\:{Q} \\ $$$$\left({intersection}\:{of}\:{circle}\:{with}\:{line}\right) \\ $$$$\left({x}−{a}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +\left({x}\mathrm{tan}\:\theta−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} −{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi \\ $$$${x}^{\mathrm{2}} \mathrm{sec}\:^{\mathrm{2}} \theta−\mathrm{2}{x}\left({s}\mathrm{cos}\:\phi+{R}\mathrm{tan}\:\theta\right)+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${PQ}=\mid{x}_{{Q}} −{x}_{{P}} \mid\mathrm{sec}\:\theta \\ $$$$\mid{x}_{{Q}} −{x}_{{P}} \mid=\sqrt{\left({x}_{{Q}} +{x}_{{P}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{{B}} {x}_{{P}} }\: \\ $$$$\Rightarrow\:{PQ}=\left(\mathrm{sec}\:\theta\right)\sqrt{\left[\frac{\mathrm{2}\left({a}\mathrm{cos}\:\phi+{R}\mathrm{tan}\:\theta\right)}{\mathrm{sec}\:^{\mathrm{2}} \theta}\right]^{\mathrm{2}} −\frac{\mathrm{4}{a}^{\mathrm{2}} }{\mathrm{sec}\:^{\mathrm{2}} \theta}}\: \\ $$$${P}\:{Q}=\mathrm{2}\sqrt{\left({a}\mathrm{cos}\:\phi+{R}\mathrm{tan}\:\theta\right)^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta−{a}^{\mathrm{2}} }\:. \\ $$
