Question Number 35496 by ajfour last updated on 19/May/18
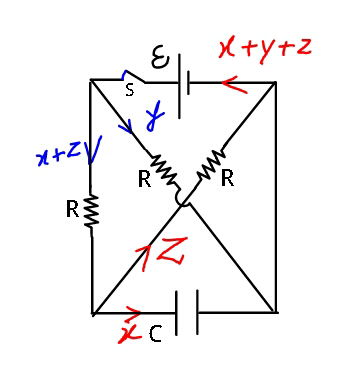
Commented by ajfour last updated on 19/May/18

$${Solution}\:{to}\:{Q}.\mathrm{35493} \\ $$
Answered by ajfour last updated on 19/May/18
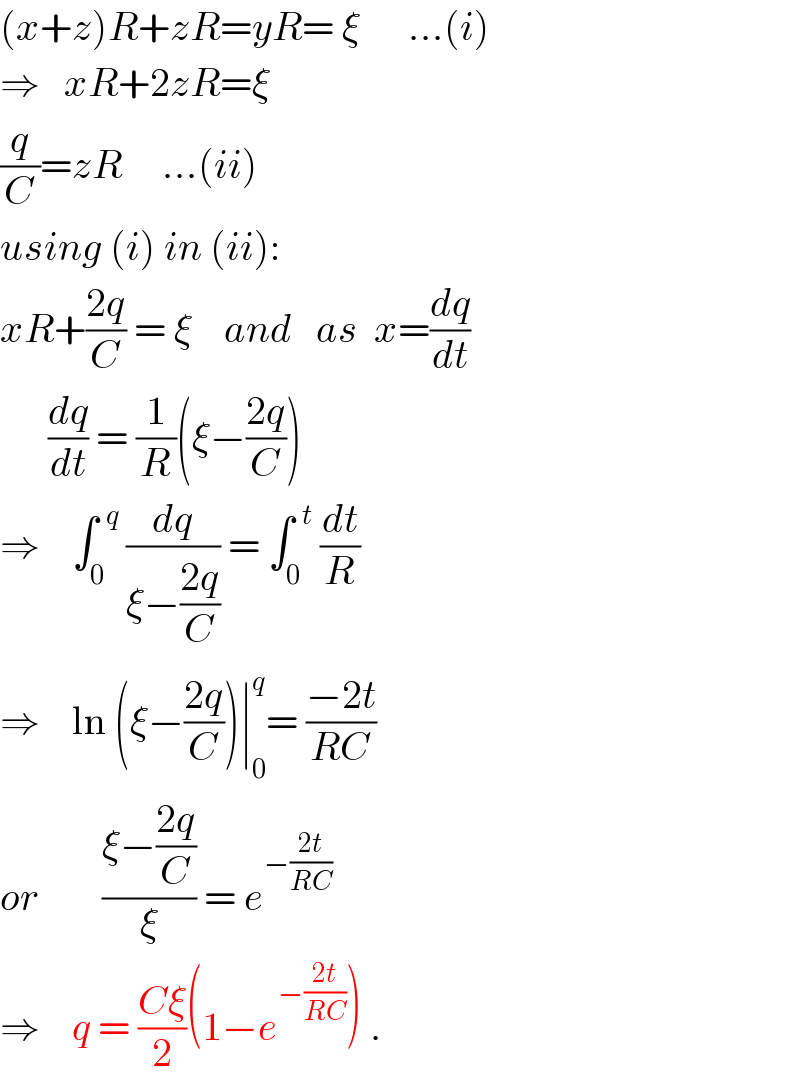
$$\left({x}+{z}\right){R}+{zR}={yR}=\:\xi\:\:\:\:\:\:…\left({i}\right) \\ $$$$\Rightarrow\:\:\:{xR}+\mathrm{2}{zR}=\xi \\ $$$$\frac{{q}}{{C}}={zR}\:\:\:\:\:…\left({ii}\right) \\ $$$${using}\:\left({i}\right)\:{in}\:\left({ii}\right): \\ $$$${xR}+\frac{\mathrm{2}{q}}{{C}}\:=\:\xi\:\:\:\:{and}\:\:\:{as}\:\:{x}=\frac{{dq}}{{dt}} \\ $$$$\:\:\:\:\:\:\frac{{dq}}{{dt}}\:=\:\frac{\mathrm{1}}{{R}}\left(\xi−\frac{\mathrm{2}{q}}{{C}}\right) \\ $$$$\Rightarrow\:\:\:\:\int_{\mathrm{0}} ^{\:\:{q}} \:\frac{{dq}}{\xi−\frac{\mathrm{2}{q}}{{C}}}\:=\:\int_{\mathrm{0}} ^{\:\:{t}} \:\frac{{dt}}{{R}} \\ $$$$\Rightarrow\:\:\:\:\mathrm{ln}\:\left(\xi−\frac{\mathrm{2}{q}}{{C}}\right)\mid_{\mathrm{0}} ^{{q}} =\:\frac{−\mathrm{2}{t}}{{RC}} \\ $$$${or}\:\:\:\:\:\:\:\:\frac{\xi−\frac{\mathrm{2}{q}}{{C}}}{\xi}\:=\:{e}^{−\frac{\mathrm{2}{t}}{{RC}}} \\ $$$$\Rightarrow\:\:\:\:{q}\:=\:\frac{{C}\xi}{\mathrm{2}}\left(\mathrm{1}−{e}^{−\frac{\mathrm{2}{t}}{{RC}}} \right)\:. \\ $$
