Question Number 35537 by Raj Singh last updated on 20/May/18

Answered by tanmay.chaudhury50@gmail.com last updated on 20/May/18
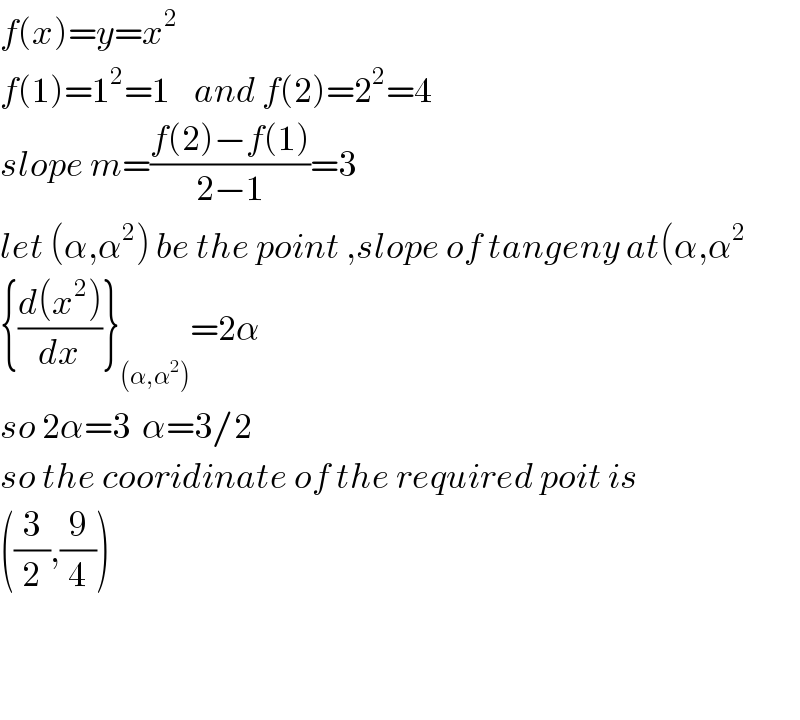
$${f}\left({x}\right)={y}={x}^{\mathrm{2}} \:\: \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}^{\mathrm{2}} =\mathrm{1}\:\:\:\:{and}\:{f}\left(\mathrm{2}\right)=\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$${slope}\:{m}=\frac{{f}\left(\mathrm{2}\right)−{f}\left(\mathrm{1}\right)}{\mathrm{2}−\mathrm{1}}=\mathrm{3} \\ $$$${let}\:\left(\alpha,\alpha^{\mathrm{2}} \right)\:{be}\:{the}\:{point}\:,{slope}\:{of}\:{tangeny}\:{at}\left(\alpha,\alpha^{\mathrm{2}} \right. \\ $$$$\left\{\frac{{d}\left({x}^{\mathrm{2}} \right)}{{dx}}\right\}_{\left(\alpha,\alpha^{\mathrm{2}} \right)} =\mathrm{2}\alpha \\ $$$${so}\:\mathrm{2}\alpha=\mathrm{3}\:\:\alpha=\mathrm{3}/\mathrm{2} \\ $$$${so}\:{the}\:{cooridinate}\:{of}\:{the}\:{required}\:{poit}\:{is} \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{9}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$ \\ $$
