Question Number 35606 by ajfour last updated on 21/May/18

Commented by ajfour last updated on 21/May/18
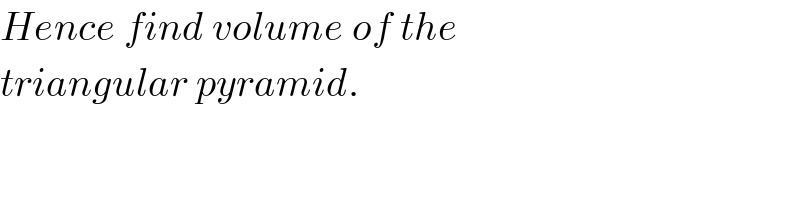
$${Hence}\:{find}\:{volume}\:{of}\:{the} \\ $$$${triangular}\:{pyramid}. \\ $$
Commented by MrW3 last updated on 04/Nov/18

$${a}={BC}=\sqrt{{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{qr}\:\mathrm{cos}\:\phi} \\ $$$${b}={CA}=\sqrt{{r}^{\mathrm{2}} +{p}^{\mathrm{2}} −\mathrm{2}{rp}\:\mathrm{cos}\:\psi} \\ $$$${c}={AB}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{pq}\:\mathrm{cos}\:\theta} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ah}_{{a}} =\frac{\mathrm{1}}{\mathrm{2}}{qr}\:\mathrm{sin}\:\phi \\ $$$$\Rightarrow{h}_{{a}} =\frac{{qr}\:\mathrm{sin}\:\phi}{{a}}=\frac{{qr}\:\mathrm{sin}\:\phi}{\:\sqrt{{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{qr}\:\mathrm{cos}\:\phi}} \\ $$$${similarly} \\ $$$$\Rightarrow{h}_{{b}} =\frac{{rp}\:\mathrm{sin}\:\psi}{\:\sqrt{{r}^{\mathrm{2}} +{p}^{\mathrm{2}} −\mathrm{2}{rp}\:\mathrm{cos}\:\psi}} \\ $$$$\Rightarrow{h}_{{c}} =\frac{{pq}\:\mathrm{sin}\:\theta}{\:\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{pq}\:\mathrm{cos}\:\theta}} \\ $$$${let}\:{h}={height}\:{of}\:{pyramid} \\ $$$${d}_{{a}} =\sqrt{{h}_{{a}} ^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$${d}_{{b}} =\sqrt{{h}_{{a}} ^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$${d}_{{c}} =\sqrt{{h}_{{c}} ^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$${let}\:{s}=\frac{{a}+{b}+{c}}{\mathrm{2}} \\ $$$${A}_{{base}} =\frac{\mathrm{1}}{\mathrm{2}}\left({ad}_{{a}} +{bd}_{{b}} +{cd}_{{c}} \right)=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$$\sqrt{{q}^{\mathrm{2}} {r}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\phi−{a}^{\mathrm{2}} {h}^{\mathrm{2}} }+\sqrt{{r}^{\mathrm{2}} {p}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\psi−{b}^{\mathrm{2}} {h}^{\mathrm{3}} }+\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta−{c}^{\mathrm{2}} {h}^{\mathrm{2}} }=\mathrm{2}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$$\Rightarrow{h} \\ $$$${V}=\frac{{h}\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}}{\mathrm{3}} \\ $$
