Question Number 35696 by Tinkutara last updated on 22/May/18
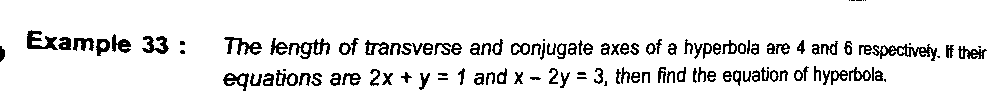
Commented by Rasheed.Sindhi last updated on 22/May/18

$$\mathrm{Mr}\:\mathrm{Tinkutara}, \\ $$$$\:^{\bullet} \mathrm{I}'\mathrm{ve}\:\mathrm{tried}\:\mathrm{many}\:\mathrm{attempts}\:\mathrm{to}\:\mathrm{your} \\ $$$$\mathrm{Q}#\mathrm{34870}.\:\mathrm{I}\:\mathrm{could}\:\mathrm{be}\:\mathrm{able}\:\mathrm{to}\:\mathrm{complete} \\ $$$$\:\mathrm{only}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{under}\:\mathrm{the}\:\mathrm{topic}, \\ $$$$'\mathrm{Pattern}\:\mathrm{approach}'.\mathrm{Other}\:\mathrm{attempts} \\ $$$$\mathrm{are}\:\mathrm{almost}\:\mathrm{deleteable}. \\ $$$$\:^{\bullet} \mathrm{I}'\mathrm{ve}\:\mathrm{produced}\:\mathrm{an}\:\mathrm{other}\:\mathrm{soution}\:\mathrm{of} \\ $$$$\:\mathrm{the}\:\mathrm{Q}#\mathrm{34760}\:\mathrm{using}\:\mathrm{hint}\:\mathrm{provided} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{question}. \\ $$$$\mathrm{Pl}\:\mathrm{see}\:\mathrm{if}\:\mathrm{you}\:\mathrm{didn}'\mathrm{t}. \\ $$
Commented by ajfour last updated on 22/May/18

Commented by ajfour last updated on 22/May/18
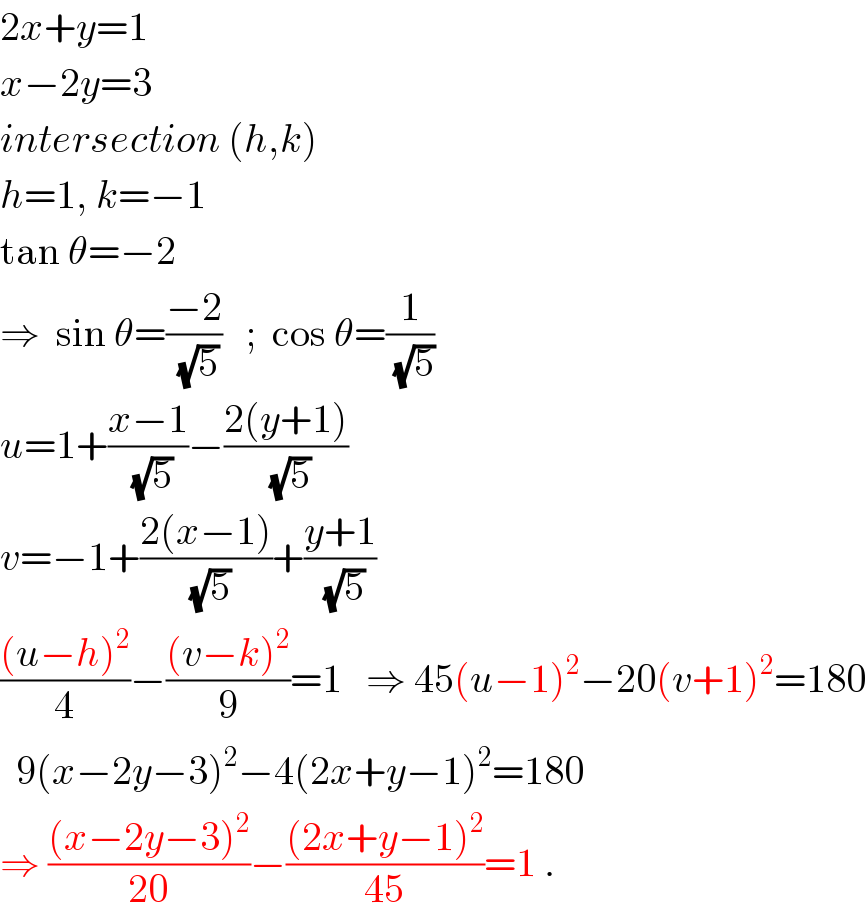
$$\mathrm{2}{x}+{y}=\mathrm{1} \\ $$$${x}−\mathrm{2}{y}=\mathrm{3} \\ $$$${intersection}\:\left({h},{k}\right) \\ $$$${h}=\mathrm{1},\:{k}=−\mathrm{1} \\ $$$$\mathrm{tan}\:\theta=−\mathrm{2} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\theta=\frac{−\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\:\:;\:\:\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${u}=\mathrm{1}+\frac{{x}−\mathrm{1}}{\:\sqrt{\mathrm{5}}}−\frac{\mathrm{2}\left({y}+\mathrm{1}\right)}{\:\sqrt{\mathrm{5}}} \\ $$$${v}=−\mathrm{1}+\frac{\mathrm{2}\left({x}−\mathrm{1}\right)}{\:\sqrt{\mathrm{5}}}+\frac{{y}+\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\frac{\left({u}−{h}\right)^{\mathrm{2}} }{\mathrm{4}}−\frac{\left({v}−{k}\right)^{\mathrm{2}} }{\mathrm{9}}=\mathrm{1}\:\:\:\Rightarrow\:\mathrm{45}\left({u}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{20}\left({v}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{180} \\ $$$$\:\:\mathrm{9}\left({x}−\mathrm{2}{y}−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{2}{x}+{y}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{180}\: \\ $$$$\Rightarrow\:\frac{\left({x}−\mathrm{2}{y}−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{20}}−\frac{\left(\mathrm{2}{x}+{y}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{45}}=\mathrm{1}\:. \\ $$
Commented by Tinkutara last updated on 22/May/18
@ajfour Sir: The answer is little wrong.
@Rasheed Sir: I also did the first case by hit and trial only. We can do it only when c given is small.
Commented by ajfour last updated on 22/May/18

$$\mathscr{T}{hanks}. \\ $$
Commented by Tinkutara last updated on 22/May/18
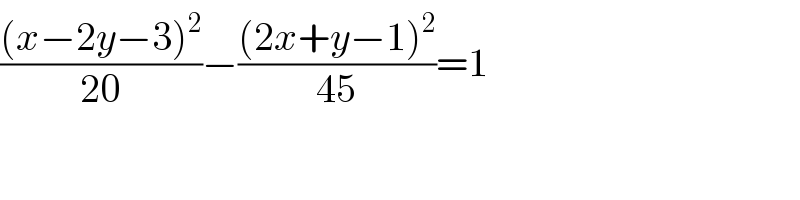
$$\frac{\left({x}−\mathrm{2}{y}−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{20}}−\frac{\left(\mathrm{2}{x}+{y}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{45}}=\mathrm{1} \\ $$
Commented by Tinkutara last updated on 22/May/18
Thanks Sir! It also has a shorter approach.
