Question Number 35750 by ajfour last updated on 23/May/18
Commented by ajfour last updated on 23/May/18

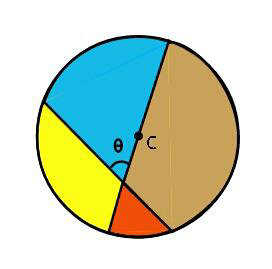
$${Find}\:{proportion}\:{of}\:{blue},\:{brown}, \\ $$$${yellow},\:{and}\:{red}\:{coloured}\:{areas}. \\ $$$${Given}:\:{chord}\:{makes}\:{angle}\:\theta\:{with} \\ $$$${the}\:{diameter}\:{shown}\:{and}\:{that}\:{the} \\ $$$${point}\:{of}\:{intersection}\:{of}\:{the}\:{chord} \\ $$$${and}\:{the}\:{diameter}\:{is}\:{at}\:{distance} \\ $$$$\boldsymbol{\lambda{r}}\:{from}\:{centre}\:{of}\:{circle}. \\ $$
Commented by ajfour last updated on 23/May/18
Commented by ajfour last updated on 23/May/18

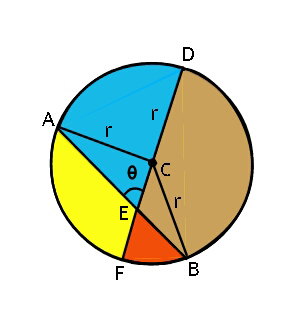
$${CE}\:=\lambda{r}\: \\ $$
Commented by ajfour last updated on 23/May/18
![AB=2(√(r^2 −λ^2 r^2 sin^2 θ)) AE= ((AB)/2)+CEcos θ =r(√(1−λ^2 sin^2 θ))+λrcos θ BE=r(√(1−λ^2 sin^2 θ))−λrcos θ Area(△ACE)=(1/2)(AE)(CE)sin θ =((λr^2 sin θ)/2)((√(1−λ^2 sin^2 θ))+λcos θ) similarly Area(△BCE)=(1/2)(BE)(CE)sin θ =((λr^2 sin θ)/2)((√(1−λ^2 sin^2 θ))−λcos θ) let sin ∠CAE =sin ∠CBE =sin α sin α =((λrsin θ)/r) =λsin θ ⇒ α=sin^(−1) (λsin θ) ∠ACD = α+θ Area(sector CAD)=(r^2 /2)(θ+α) −−−−−−−−−−−−−−− Area(blue)=Area(△ACE)+ Area(sector CAD) =((λr^2 sin θ)/2)((√(1−λ^2 sin^2 θ))+λcos θ) +(r^2 /2)[θ+sin^(−1) (λsin θ)] −−−−−−−−−−−−−−− Area(yellow)=Area(sector ACF) −Area(△ACE) =(r^2 /2)[π−θ−sin^(−1) (λsin θ)] − ((λr^2 sin θ)/2)((√(1−λ^2 sin^2 θ))+λcos θ) −−−−−−−−−−−−−−− Area(△BCE) =((λr^2 sin θ)/2)((√(1−λ^2 sin^2 θ))−λcos θ) Area(brown)=(r^2 /2)(π−θ+α) +Area(△BCE) =(r^2 /2)[π−θ+sin^(−1) (λsin θ)] +((λr^2 sin θ)/2)((√(1−λ^2 sin^2 θ))−λcos θ) −−−−−−−−−−−−−−− Area(red)=(r^2 /2)[θ−sin^(−1) (λsin θ)] −((λr^2 sin θ)/2)((√(1−λ^2 sin^2 θ))−λcos θ) −−−−−−−−−−−−−−−.](https://www.tinkutara.com/question/Q35770.png)
$${AB}=\mathrm{2}\sqrt{{r}^{\mathrm{2}} −\lambda^{\mathrm{2}} {r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$${AE}=\:\frac{{AB}}{\mathrm{2}}+{CE}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:={r}\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}+\lambda{r}\mathrm{cos}\:\theta \\ $$$${BE}={r}\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}−\lambda{r}\mathrm{cos}\:\theta \\ $$$${Area}\left(\bigtriangleup{ACE}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({AE}\right)\left({CE}\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:=\frac{\lambda{r}^{\mathrm{2}} \mathrm{sin}\:\theta}{\mathrm{2}}\left(\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}+\lambda\mathrm{cos}\:\theta\right) \\ $$$${similarly} \\ $$$$\:{Area}\left(\bigtriangleup{BCE}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({BE}\right)\left({CE}\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:=\frac{\lambda{r}^{\mathrm{2}} \mathrm{sin}\:\theta}{\mathrm{2}}\left(\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}−\lambda\mathrm{cos}\:\theta\right) \\ $$$${let}\:\:\mathrm{sin}\:\angle{CAE}\:=\mathrm{sin}\:\angle{CBE}\:=\mathrm{sin}\:\alpha \\ $$$$\mathrm{sin}\:\alpha\:=\frac{\lambda{r}\mathrm{sin}\:\theta}{{r}}\:=\lambda\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\alpha=\mathrm{sin}^{−\mathrm{1}} \left(\lambda\mathrm{sin}\:\theta\right) \\ $$$$\angle{ACD}\:=\:\alpha+\theta \\ $$$${Area}\left({sector}\:{CAD}\right)=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\theta+\alpha\right) \\ $$$$−−−−−−−−−−−−−−− \\ $$$${Area}\left({blue}\right)={Area}\left(\bigtriangleup{ACE}\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Area}\left({sector}\:{CAD}\right) \\ $$$$\:\:\:=\frac{\lambda{r}^{\mathrm{2}} \mathrm{sin}\:\theta}{\mathrm{2}}\left(\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}+\lambda\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left[\theta+\mathrm{sin}^{−\mathrm{1}} \left(\lambda\mathrm{sin}\:\theta\right)\right] \\ $$$$−−−−−−−−−−−−−−− \\ $$$${Area}\left({yellow}\right)={Area}\left({sector}\:{ACF}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{Area}\left(\bigtriangleup{ACE}\right) \\ $$$$\:\:=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left[\pi−\theta−\mathrm{sin}^{−\mathrm{1}} \left(\lambda\mathrm{sin}\:\theta\right)\right] \\ $$$$\:\:\:−\:\frac{\lambda{r}^{\mathrm{2}} \mathrm{sin}\:\theta}{\mathrm{2}}\left(\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}+\lambda\mathrm{cos}\:\theta\right) \\ $$$$−−−−−−−−−−−−−−− \\ $$$${Area}\left(\bigtriangleup{BCE}\right) \\ $$$$\:\:=\frac{\lambda{r}^{\mathrm{2}} \mathrm{sin}\:\theta}{\mathrm{2}}\left(\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}−\lambda\mathrm{cos}\:\theta\right) \\ $$$${Area}\left({brown}\right)=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\pi−\theta+\alpha\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{Area}\left(\bigtriangleup{BCE}\right) \\ $$$$\:\:\:\:=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left[\pi−\theta+\mathrm{sin}^{−\mathrm{1}} \left(\lambda\mathrm{sin}\:\theta\right)\right] \\ $$$$\:\:\:\:+\frac{\lambda{r}^{\mathrm{2}} \mathrm{sin}\:\theta}{\mathrm{2}}\left(\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}−\lambda\mathrm{cos}\:\theta\right) \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\:\:{Area}\left({red}\right)=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left[\theta−\mathrm{sin}^{−\mathrm{1}} \left(\lambda\mathrm{sin}\:\theta\right)\right] \\ $$$$\:\:\:−\frac{\lambda{r}^{\mathrm{2}} \mathrm{sin}\:\theta}{\mathrm{2}}\left(\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}−\lambda\mathrm{cos}\:\theta\right) \\ $$$$−−−−−−−−−−−−−−−. \\ $$
