Question Number 35763 by $@ty@m last updated on 23/May/18
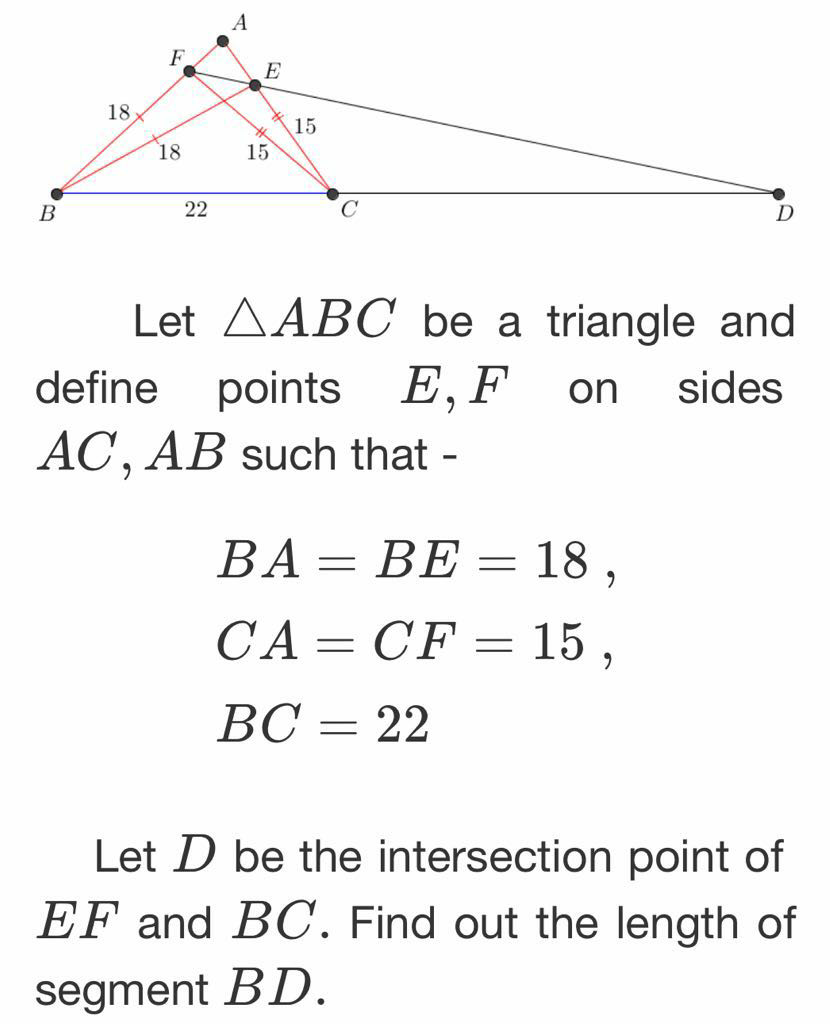
Answered by ajfour last updated on 23/May/18

$${let}\:\angle{BDF}\:=\:\alpha \\ $$$${AF}=\mathrm{30cos}\:{A}\:\:;\:\:\:{AE}=\mathrm{36cos}\:{A} \\ $$$$\mathrm{cot}\:\alpha\:=\:\frac{{AF}\mathrm{cos}\:{B}+{AE}\mathrm{cos}\:{C}}{{BF}\mathrm{sin}\:{B}−{CE}\mathrm{sin}\:{C}} \\ $$$$\:\:\:=\frac{\mathrm{30cos}\:{A}\mathrm{cos}\:{B}+\mathrm{36cos}\:{A}\mathrm{cos}\:{C}}{\left(\mathrm{18}−\mathrm{30cos}\:{A}\right)\mathrm{sin}\:{B}−\left(\mathrm{15}−\mathrm{36cos}\:{A}\right)\mathrm{sin}\:{C}} \\ $$$${BD}={BF}\mathrm{cos}\:{B}+{BF}\mathrm{sin}\:{B}\mathrm{cot}\:\alpha \\ $$$$\:\:\:\:\:\:{where}\:\:\:{BF}\:=\:\mathrm{18}−\mathrm{30cos}\:{A} \\ $$$$\mathrm{cos}\:{A},\:\:\mathrm{sin}\:{B},\:\mathrm{cos}\:{B},\:\mathrm{sin}\:{C},\:\mathrm{cos}\:{C} \\ $$$${can}\:{be}\:{evaluated}\:{from}\:{the}\:{known} \\ $$$${values}\:{of}\:{the}\:{sides}\:{of}\:{the}\:\bigtriangleup{ABC}. \\ $$
Commented by $@ty@m last updated on 23/May/18

$${Thanks}\:{a}\:{lot}! \\ $$
