Question-35769

Question Number 35769 by Tinkutara last updated on 23/May/18

Answered by ajfour last updated on 23/May/18

let f(x)=((2x)/(1+x^2 )) ((df(x))/dx)=((2(1+x^2 )−4x^2 )/((1+x^2 )^2 )) = ((2(1−x)(1+x))/((1+x^2 )^2 )) ⇒ f(x)_(min) = f(−1) = −1 f(x)_(max) =f(1) = 1 Hence y=tan^(−1) [f(x)] has range ∈ [−(π/4) , (π/4)] .

$${let}\:\:{f}\left({x}\right)=\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\frac{{df}\left({x}\right)}{{dx}}=\frac{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\mathrm{4}{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\:\frac{\mathrm{2}\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:{f}\left({x}\right)_{{min}} =\:{f}\left(−\mathrm{1}\right)\:=\:−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{f}\left({x}\right)_{{max}} ={f}\left(\mathrm{1}\right)\:=\:\mathrm{1} \\ $$$${Hence}\:\:{y}=\mathrm{tan}^{−\mathrm{1}} \left[{f}\left({x}\right)\right]\:{has}\:{range} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\in\:\left[−\frac{\pi}{\mathrm{4}}\:,\:\frac{\pi}{\mathrm{4}}\right]\:. \\ $$

Commented by Tinkutara last updated on 23/May/18

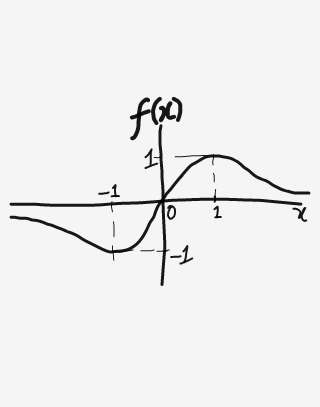
Is f(x) increasing or decreasing continuously?

Commented by ajfour last updated on 23/May/18

decreasing, then increasing, then again decreasing.

Commented by Tinkutara last updated on 23/May/18

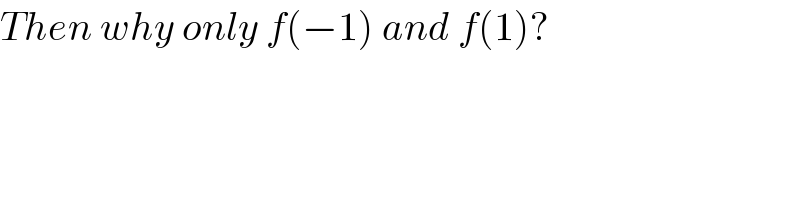
$${Then}\:{why}\:{only}\:{f}\left(−\mathrm{1}\right)\:{and}\:{f}\left(\mathrm{1}\right)? \\ $$

Commented by ajfour last updated on 23/May/18

Commented by Tinkutara last updated on 23/May/18

Thank you very much Sir! I got the answer. ��

Answered by tanmay.chaudhury50@gmail.com last updated on 24/May/18

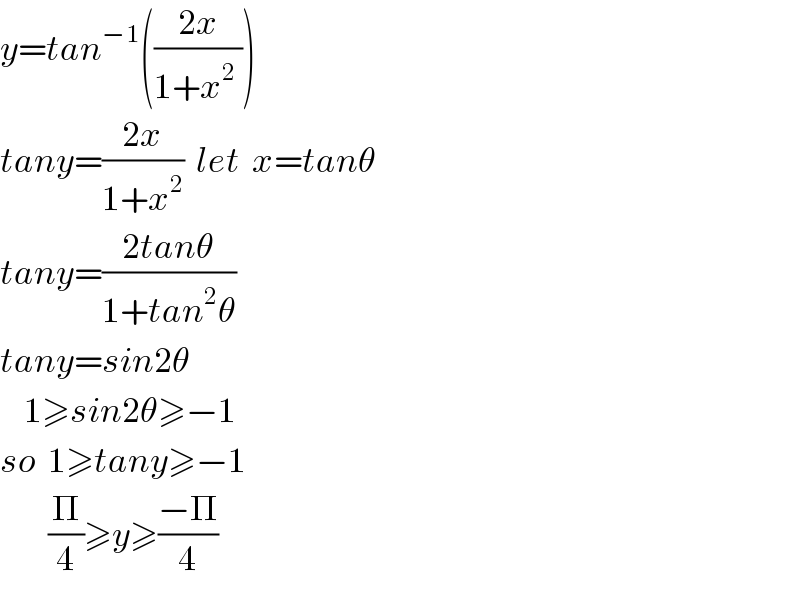
y=tan^(−1) (((2x)/(1+x^2 ))) tany=((2x)/(1+x^2 )) let x=tanθ tany=((2tanθ)/(1+tan^2 θ)) tany=sin2θ 1≥sin2θ≥−1 so 1≥tany≥−1 (Π/4)≥y≥((−Π)/4)

$${y}={tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} \:}\right) \\ $$$${tany}=\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:{let}\:\:{x}={tan}\theta \\ $$$${tany}=\frac{\mathrm{2}{tan}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta} \\ $$$${tany}={sin}\mathrm{2}\theta \\ $$$$\:\:\:\:\mathrm{1}\geqslant{sin}\mathrm{2}\theta\geqslant−\mathrm{1} \\ $$$${so}\:\:\mathrm{1}\geqslant{tany}\geqslant−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\frac{\Pi}{\mathrm{4}}\geqslant{y}\geqslant\frac{−\Pi}{\mathrm{4}} \\ $$

Commented by Tinkutara last updated on 24/May/18

Thank you very much Sir! I got the answer. �� Nice method.

Facebook Tweet Pin

Leave a Reply Cancel reply