Question Number 35828 by ajfour last updated on 24/May/18
Commented by ajfour last updated on 24/May/18

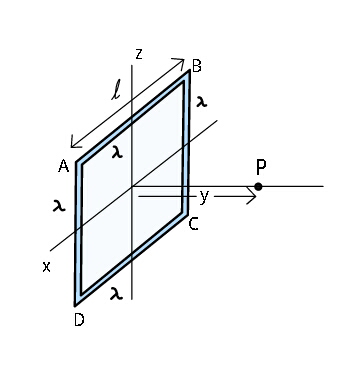
$${Find}\:{the}\:{electric}\:{field}\:{at}\:{point}\:{P} \\ $$$${on}\:{the}\:{y}\:{axis}\:{at}\:{a}\:{distance}\:{y}\:{from} \\ $$$${origin}\:{due}\:{to}\:{a}\:{uniformly}\:{charged} \\ $$$${square}\:{wire}\:{frame}\:{of}\:{linear}\:{charge} \\ $$$${density}\:\lambda.\:{The}\:{frame}\:{lies}\:{in}\:{xz} \\ $$$${plane}\:{with}\:{sides}\:{of}\:{frame}\://\:{to} \\ $$$${x}\:{and}\:{z}\:{axis}\:{with}\:{centre}\:{of}\:{frame} \\ $$$${at}\:{origin}. \\ $$
Commented by ajfour last updated on 24/May/18

$${Can}\:{we}\:{also}\:{find}\:{Electric}\:{Potential} \\ $$$${at}\:{an}\:{arbitrary}\:{point}\:{P}\:\left({x},{y},{z}\right) \\ $$$${and}\:{hence}\:{find}\:{Electric}\:{field}\:{too} \\ $$$${by}\:{taking}\:{partial}\:{derivatives}\:? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/May/18
![let from mid point of AB at a distance x we consider dx elemetary length. charge in dx element=λdx electricfield at p is dE=(1/(4Πε_0 ))×((λdx)/({((l/2))^2 +x^2 +y^2 })) effective dE is dEcosθ cosθ=(y/( (√(((l/2))^2 +x^2 +y^(2 _ ) )))) (dE)_e =(1/(4Πε_0 ))×((λdx)/({((l/2))^2 +x^2 +y^2 }))×(y/( (√(((l/2))^2 +x^2 +y^2 )))) (dE)_e =(1/(4Πε_0 ))×((λydx)/({((l/2))^2 +y^2 +x^2 }^(3/2) )) (E)_e =((λy)/(4Πε_0 ))∫_((−l)/2) ^(l/2) (dx/({((l/2))^2 +y^2 +x^2 }^(3/2) )) supose the value of this intregation is I same result for BC,CD,DA so Eletric field at P for ABCD is 4I give me time to solve the intregal see the method... let I′=∫(dx/({((l/2))^2 +y^2 +x^2 }^(3/2) )) let x={(√(((l/2))^2 +y^2 )) } tanθ dx={(√(((l/2))^2 +y^2 )) }sec^2 θ dθ ∫(({(√(((l/2))^2 +y^2 ))}sec^2 θ dθ)/([{((l/2))^2 +y^2 }sec^2 θ]^(3/2) )) =(1/({((l/2))^2 +y^2 }))×∫(dθ/(secθ)) =(1/({((l/2))^2 +y^2 }))×sinθ =(1/({((l/2))^2 +y^2 }))×(x/({((l/2))^2 +y^2 +x^2 }^(1/2) )) nos putting the limits =(1/({((l/2))^2 +y^2 }))×∣(x/({((l/2))^2 +y^2 +x^2 }^(1/2) ))∣_(−(l/2)) ^(l/2) =(1/({((l/2))^2 +y^2 }))×(l/({((l/2))^2 +y^2 +((l/2))^2 }^(1/2) )) =(1/({((l/2))^2 +y^2 }))×(l/({(l^2 /2)+y^2 }^((1/2) ) )) hence required electric field is =4×((λy)/(4Πε_0 ))×(1/({((l/2))^2 +y^2 }))×(l/({(l^2 /2)+y^2 }^(1/2) ))](https://www.tinkutara.com/question/Q35831.png)
$${let}\:{from}\:{mid}\:{point}\:{of}\:{AB}\:{at}\:{a}\:{distance}\:{x}\:{we} \\ $$$${consider}\:{dx}\:{elemetary}\:{length}.\:{charge}\:{in}\:{dx} \\ $$$${element}=\lambda{dx} \\ $$$${electricfield}\:{at}\:{p}\:{is} \\ $$$${dE}=\frac{\mathrm{1}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\frac{\lambda{dx}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}} \\ $$$${effective}\:{dE}\:{is}\:{dEcos}\theta \\ $$$${cos}\theta=\frac{{y}}{\:\sqrt{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} +{y}^{\mathrm{2}\:_{\:} } }} \\ $$$$\left({dE}\right)_{{e}} =\frac{\mathrm{1}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\frac{\lambda{dx}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}}×\frac{{y}}{\:\sqrt{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }} \\ $$$$\left({dE}\right)_{{e}} =\frac{\mathrm{1}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\frac{\lambda{ydx}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \right\}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\left({E}\right)_{{e}} =\frac{\lambda{y}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }\int_{\frac{−{l}}{\mathrm{2}}} ^{\frac{{l}}{\mathrm{2}}} \:\frac{{dx}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \right\}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${supose}\:{the}\:{value}\:{of}\:{this}\:{intregation}\:{is}\:{I} \\ $$$${same}\:{result}\:{for}\:{BC},{CD},{DA} \\ $$$${so}\:{Eletric}\:{field}\:{at}\:{P}\:{for}\:{ABCD}\:{is}\:\mathrm{4}{I} \\ $$$${give}\:{me}\:{time}\:{to}\:{solve}\:{the}\:{intregal} \\ $$$${see}\:{the}\:{method}… \\ $$$${let}\:\:{I}'=\int\frac{{dx}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \:\right\}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${let}\:{x}=\left\{\sqrt{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\right\}\:{tan}\theta \\ $$$${dx}=\left\{\sqrt{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:\right\}{sec}^{\mathrm{2}} \theta\:{d}\theta \\ $$$$\int\frac{\left\{\sqrt{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\right\}{sec}^{\mathrm{2}} \theta\:{d}\theta}{\left[\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}{sec}^{\mathrm{2}} \theta\right]^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{\mathrm{1}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}}×\int\frac{{d}\theta}{{sec}\theta} \\ $$$$=\frac{\mathrm{1}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}}×{sin}\theta \\ $$$$=\frac{\mathrm{1}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}}×\frac{{x}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \right\}^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$${nos}\:{putting}\:{the}\:{limits} \\ $$$$=\frac{\mathrm{1}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}}×\mid\frac{{x}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}^{\mathrm{2}} \right\}^{\frac{\mathrm{1}}{\mathrm{2}}} }\mid_{−\frac{{l}}{\mathrm{2}}} ^{\frac{{l}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}}×\frac{{l}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} \right\}^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$=\frac{\mathrm{1}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}}×\frac{{l}}{\left\{\frac{{l}^{\mathrm{2}} }{\mathrm{2}}+{y}^{\mathrm{2}} \right\}^{\frac{\mathrm{1}}{\mathrm{2}}\:} } \\ $$$${hence}\:{required}\:{electric}\:{field}\:{is} \\ $$$$=\mathrm{4}×\frac{\lambda{y}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\frac{\mathrm{1}}{\left\{\left(\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \right\}}×\frac{{l}}{\left\{\frac{{l}^{\mathrm{2}} }{\mathrm{2}}+{y}^{\mathrm{2}} \right\}^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 25/May/18

$${you}\:{are}\:{a}\:{train}\:{and}\:{the}\:{train}\:{must}\:{finich}\:{his} \\ $$$${road}…. \\ $$
Commented by ajfour last updated on 24/May/18
$${Beautiful}\:!\:{Thanks}\:{Tanmay}\:{Sir}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 24/May/18

$${i}\:{am}\:{govt}\:{employee}…{interested}\:{in}\:{physics} \\ $$$${and}\:{math}…{food}\:{of}\:{brain}.. \\ $$
