Question-35844

Question Number 35844 by behi83417@gmail.com last updated on 24/May/18

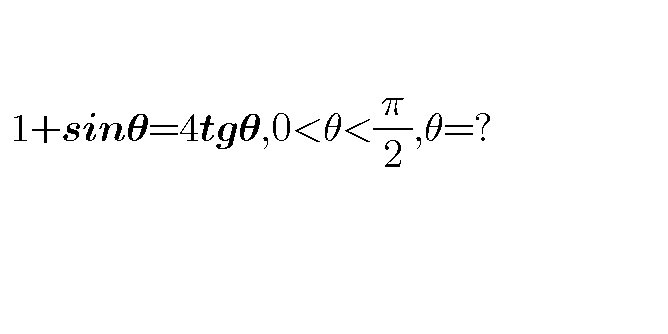
Commented by abdo mathsup 649 cc last updated on 30/May/18

let put θ =arctant with t>0 (e)⇔ 1+sin(arctant) =4t ⇔ 1+ (t/( (√(1+t^2 )))) =4t ⇔ t +(√(1+t^2 )) =4t(√(1+t^2 )) ⇔ t =(4t−1)(√(1+t^2 )) ⇔t^2 =(4t−1)^2 (1+t^2 ) ⇔ t^2 =(16t^2 −8t +1)(1+t^2 ) ⇔t^2 =16t^2 −8t +1 +16 t^4 −8t^3 +t^2 ⇔ 16 t^4 −8t^3 +16 t^2 −8t +1 =0 ...be continued...

$${let}\:{put}\:\theta\:={arctant}\:\:{with}\:{t}>\mathrm{0} \\ $$$$\left({e}\right)\Leftrightarrow\:\mathrm{1}+{sin}\left({arctant}\right)\:=\mathrm{4}{t}\:\Leftrightarrow \\ $$$$\mathrm{1}+\:\frac{{t}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:=\mathrm{4}{t}\:\Leftrightarrow\:{t}\:+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\:=\mathrm{4}{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\:{t}\:\:=\left(\mathrm{4}{t}−\mathrm{1}\right)\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Leftrightarrow{t}^{\mathrm{2}} \:=\left(\mathrm{4}{t}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\:{t}^{\mathrm{2}} \:=\left(\mathrm{16}{t}^{\mathrm{2}} −\mathrm{8}{t}\:+\mathrm{1}\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow{t}^{\mathrm{2}} \:=\mathrm{16}{t}^{\mathrm{2}} \:−\mathrm{8}{t}\:+\mathrm{1}\:+\mathrm{16}\:{t}^{\mathrm{4}} \:−\mathrm{8}{t}^{\mathrm{3}} \:+{t}^{\mathrm{2}} \\ $$$$\Leftrightarrow\:\mathrm{16}\:{t}^{\mathrm{4}} \:−\mathrm{8}{t}^{\mathrm{3}} \:+\mathrm{16}\:{t}^{\mathrm{2}} \:−\mathrm{8}{t}\:+\mathrm{1}\:=\mathrm{0}\:…{be}\:{continued}… \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 25/May/18

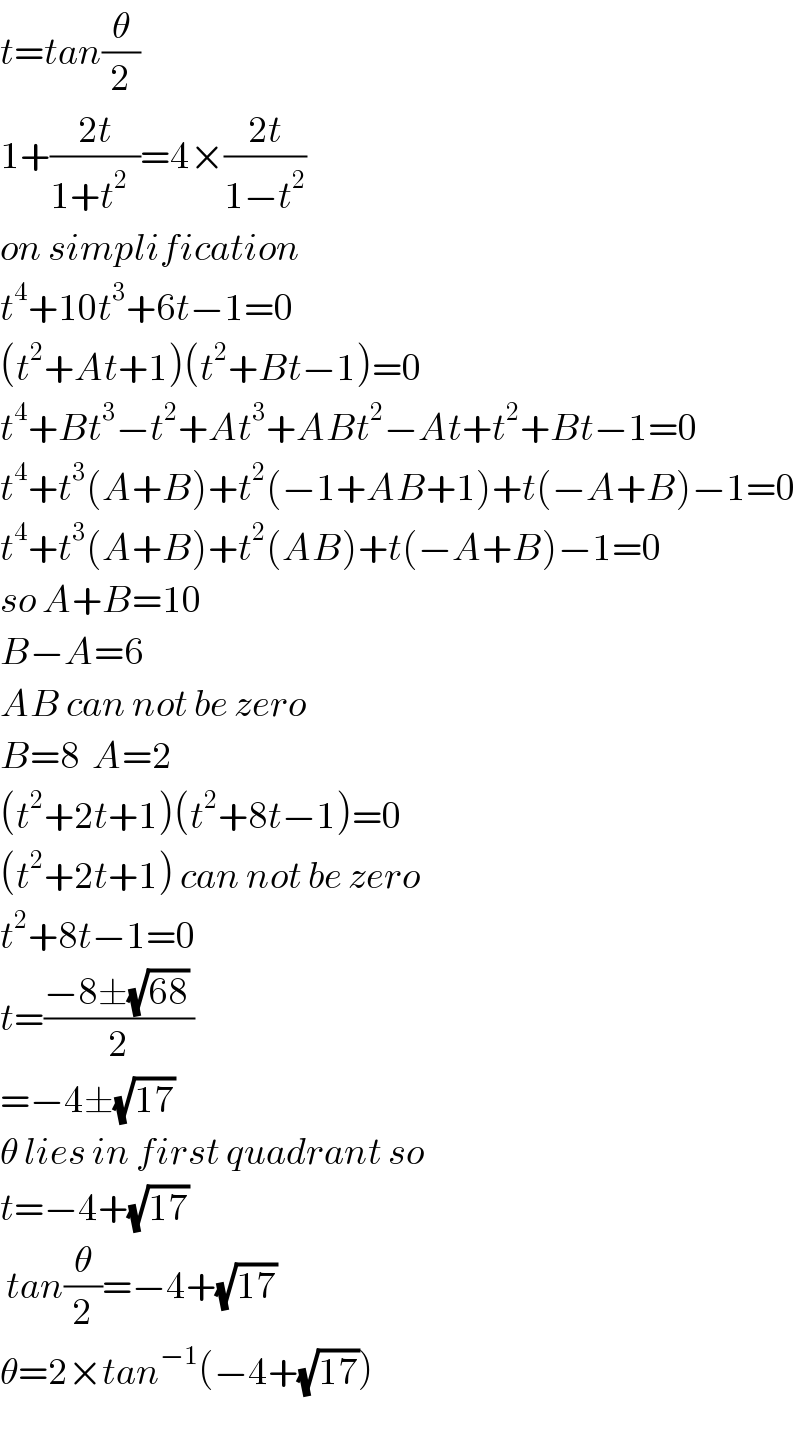
t=tan(θ/2) 1+((2t)/(1+t^(2 ) ))=4×((2t)/(1−t^2 )) on simplification t^4 +10t^3 +6t−1=0 (t^2 +At+1)(t^2 +Bt−1)=0 t^4 +Bt^3 −t^2 +At^3 +ABt^2 −At+t^2 +Bt−1=0 t^4 +t^3 (A+B)+t^2 (−1+AB+1)+t(−A+B)−1=0 t^4 +t^3 (A+B)+t^2 (AB)+t(−A+B)−1=0 so A+B=10 B−A=6 AB can not be zero B=8 A=2 (t^2 +2t+1)(t^2 +8t−1)=0 (t^2 +2t+1) can not be zero t^2 +8t−1=0 t=((−8±(√(68)) )/2) =−4±(√(17)) θ lies in first quadrant so t=−4+(√(17)) tan(θ/2)=−4+(√(17)) θ=2×tan^(−1) (−4+(√(17)))

$${t}={tan}\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}\:\:\:} }=\mathrm{4}×\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$${on}\:{simplification}\: \\ $$$${t}^{\mathrm{4}} +\mathrm{10}{t}^{\mathrm{3}} +\mathrm{6}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} +{At}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +{Bt}−\mathrm{1}\right)=\mathrm{0} \\ $$$${t}^{\mathrm{4}} +{Bt}^{\mathrm{3}} −{t}^{\mathrm{2}} +{At}^{\mathrm{3}} +{ABt}^{\mathrm{2}} −{At}+{t}^{\mathrm{2}} +{Bt}−\mathrm{1}=\mathrm{0} \\ $$$${t}^{\mathrm{4}} +{t}^{\mathrm{3}} \left({A}+{B}\right)+{t}^{\mathrm{2}} \left(−\mathrm{1}+{AB}+\mathrm{1}\right)+{t}\left(−{A}+{B}\right)−\mathrm{1}=\mathrm{0} \\ $$$${t}^{\mathrm{4}} +{t}^{\mathrm{3}} \left({A}+{B}\right)+{t}^{\mathrm{2}} \left({AB}\right)+{t}\left(−{A}+{B}\right)−\mathrm{1}=\mathrm{0} \\ $$$${so}\:{A}+{B}=\mathrm{10} \\ $$$${B}−{A}=\mathrm{6} \\ $$$${AB}\:{can}\:{not}\:{be}\:{zero} \\ $$$${B}=\mathrm{8}\:\:{A}=\mathrm{2} \\ $$$$\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{8}{t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)\:{can}\:{not}\:{be}\:{zero} \\ $$$${t}^{\mathrm{2}} +\mathrm{8}{t}−\mathrm{1}=\mathrm{0} \\ $$$${t}=\frac{−\mathrm{8}\pm\sqrt{\mathrm{68}}\:}{\mathrm{2}} \\ $$$$=−\mathrm{4}\pm\sqrt{\mathrm{17}} \\ $$$$\theta\:{lies}\:{in}\:{first}\:{quadrant}\:{so} \\ $$$${t}=−\mathrm{4}+\sqrt{\mathrm{17}}\: \\ $$$$\:{tan}\frac{\theta}{\mathrm{2}}=−\mathrm{4}+\sqrt{\mathrm{17}}\: \\ $$$$\theta=\mathrm{2}×{tan}^{−\mathrm{1}} \left(−\mathrm{4}+\sqrt{\mathrm{17}}\right)\:\: \\ $$

Commented by Rasheed.Sindhi last updated on 25/May/18

$$\vee\in\mathbb{R}\lambda\:\mathbb{N}{i}\mathbb{C}{e}! \\ $$

Commented by behi83417@gmail.com last updated on 25/May/18

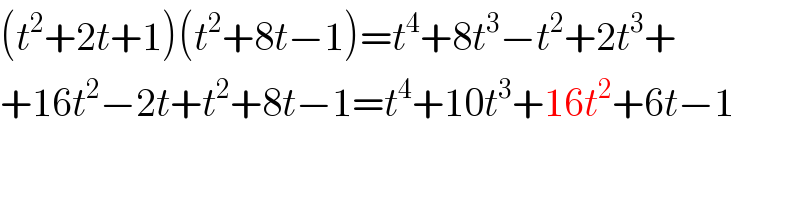
(t^2 +2t+1)(t^2 +8t−1)=t^4 +8t^3 −t^2 +2t^3 + +16t^2 −2t+t^2 +8t−1=t^4 +10t^3 +16t^2 +6t−1

$$\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{8}{t}−\mathrm{1}\right)={t}^{\mathrm{4}} +\mathrm{8}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} +\mathrm{2}{t}^{\mathrm{3}} + \\ $$$$+\mathrm{16}{t}^{\mathrm{2}} −\mathrm{2}{t}+{t}^{\mathrm{2}} +\mathrm{8}{t}−\mathrm{1}={t}^{\mathrm{4}} +\mathrm{10}{t}^{\mathrm{3}} +\mathrm{16}{t}^{\mathrm{2}} +\mathrm{6}{t}−\mathrm{1} \\ $$

Commented by ajfour last updated on 25/May/18

$${Excellent}\:{Sir},\:{i}\:{had}\:{this}\:{in}\:{mind}, \\ $$$${couldn}'{t}\:{find}\:{the}\:{time}\:{n}\:{courage}. \\ $$

Commented by behi83417@gmail.com last updated on 25/May/18

Commented by tanmay.chaudhury50@gmail.com last updated on 25/May/18

$${hanks}… \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 25/May/18

$${this}\:{method}\:{of}\:{solve}\:{may}\:{be}\:{the}\:{paradox} \\ $$$${of}\:{mathematics}\:{as}\:{Mr}.{Behi}\:\:{detected}\:{the}\:{flaw} \\ $$

Commented by Rasheed.Sindhi last updated on 26/May/18

tanmay Sir I don′t think that your method is paradox. Actually your answer suggest AB=0 also,which you didn′t consider.

$$\mathrm{tanmay}\:\mathrm{Sir} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{that}\:\mathrm{your}\:\mathrm{method}\:\mathrm{is}\:\mathrm{paradox}. \\ $$$$\mathrm{Actually}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{suggest}\:\mathrm{AB}=\mathrm{0} \\ $$$$\mathrm{also},\mathrm{which}\:\mathrm{you}\:\mathrm{didn}'\mathrm{t}\:\mathrm{consider}. \\ $$

Commented by Rasheed.Sindhi last updated on 26/May/18

A+B=10 ∧ B−A=6 ∧ AB=0 There aren′t any values which satisfy all these equations simultaneously. If these all condions were satisfied by by some values simultaneously,your method might yeild correct result. So the method is not a paradox!

$$\:\:\mathrm{A}+\mathrm{B}=\mathrm{10}\:\wedge\:\mathrm{B}−\mathrm{A}=\mathrm{6}\:\wedge\:\mathrm{AB}=\mathrm{0} \\ $$$$\mathrm{There}\:\mathrm{aren}'\mathrm{t}\:\mathrm{any}\:\mathrm{values}\:\mathrm{which}\:\mathrm{satisfy} \\ $$$$\mathrm{all}\:\mathrm{these}\:\mathrm{equations}\:\mathrm{simultaneously}. \\ $$$$\mathrm{If}\:\mathrm{these}\:\mathrm{all}\:\mathrm{condions}\:\mathrm{were}\:\mathrm{satisfied}\:\mathrm{by} \\ $$$$\mathrm{by}\:\mathrm{some}\:\mathrm{values}\:\mathrm{simultaneously},\mathrm{your} \\ $$$$\mathrm{method}\:\mathrm{might}\:\mathrm{yeild}\:\mathrm{correct}\:\mathrm{result}. \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{method}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{paradox}! \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 26/May/18

$${thank}\:{you}..{i}\:{thought}\:{i}\:{made}\:{a}\:{huge}\:{mkstake}.. \\ $$

Commented by behi83417@gmail.com last updated on 26/May/18

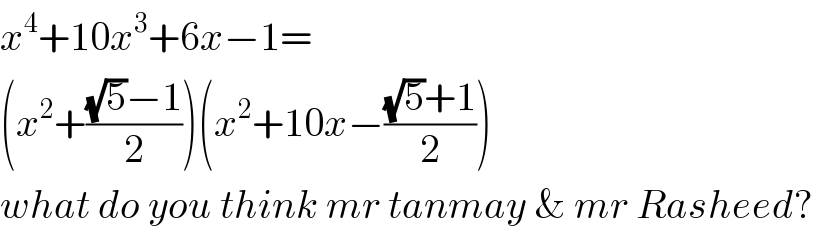
x^4 +10x^3 +6x−1= (x^2 +(((√5)−1)/2))(x^2 +10x−(((√5)+1)/2)) what do you think mr tanmay & mr Rasheed?

$${x}^{\mathrm{4}} +\mathrm{10}{x}^{\mathrm{3}} +\mathrm{6}{x}−\mathrm{1}= \\ $$$$\left({x}^{\mathrm{2}} +\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\left({x}^{\mathrm{2}} +\mathrm{10}{x}−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right) \\ $$$${what}\:{do}\:{you}\:{think}\:{mr}\:{tanmay}\:\&\:{mr}\:{Rasheed}? \\ $$

Commented by Rasheed.Sindhi last updated on 27/May/18

What method did you use to factorize? The method Mr tanmay used is failed in this particular case.

$$\mathrm{What}\:\mathrm{method}\:\mathrm{did}\:\mathrm{you}\:\mathrm{use}\:\mathrm{to}\:\mathrm{factorize}? \\ $$$$\mathrm{The}\:\mathrm{method}\:\mathrm{Mr}\:\mathrm{tanmay}\:\mathrm{used}\:\mathrm{is}\:\mathrm{failed} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{particular}\:\mathrm{case}. \\ $$

Commented by $@ty@m last updated on 27/May/18

In fact it is wrong to assume that the quadratic factors have 1 and −1 as constant terms. The product of two irratioal numbers may also yield 1 as in the present case.

$${In}\:{fact}\:{it}\:{is}\:{wrong}\:{to}\:{assume}\:{that} \\ $$$${the}\:{quadratic}\:{factors}\:{have}\:\mathrm{1}\:{and}\:−\mathrm{1} \\ $$$${as}\:{constant}\:{terms}. \\ $$$${The}\:{product}\:{of}\:{two}\:{irratioal} \\ $$$${numbers}\:{may}\:{also}\:{yield}\:\mathrm{1}\:{as}\:{in} \\ $$$${the}\:{present}\:{case}. \\ $$

Commented by Rasheed.Sindhi last updated on 27/May/18

Good approach sir, But (ii) should be,I think ab+ac+ad+bc+bd+cd=0 instead of (a+b)(c+d)=0 ...If coefficient of the highest term is unity: The sum of the products of the roots, taken two at a time,is equal to the coefficient of the third term.

$$\mathrm{Good}\:\mathrm{approach}\:\mathrm{sir}, \\ $$$$\mathrm{But}\:\left({ii}\right)\:\mathrm{should}\:\mathrm{be},\mathrm{I}\:\mathrm{think} \\ $$$${ab}+{ac}+{ad}+{bc}+{bd}+{cd}=\mathrm{0} \\ $$$$\mathrm{instead}\:\mathrm{of} \\ $$$$\left({a}+{b}\right)\left({c}+{d}\right)=\mathrm{0}\: \\ $$$$…{If}\:{coefficient}\:{of}\:{the}\:{highest}\:{term}\:{is} \\ $$$${unity}: \\ $$$${The}\:{sum}\:{of}\:{the}\:{products}\:{of}\:{the}\:{roots}, \\ $$$${taken}\:{two}\:{at}\:{a}\:{time},{is}\:{equal}\:{to}\:{the} \\ $$$${coefficient}\:{of}\:{the}\:{third}\:{term}. \\ $$

Commented by Rasheed.Sindhi last updated on 27/May/18

t^4 +10t^3 +6t−1=0 If one root is(√((3/5) ))i ((√((3/5) ))i )^4 +10((√((3/5) ))i )^3 +6((√((3/5) ))i )−1=0 (9/(25))+10((√((3/5) ))i )((√((3/5) ))i )^2 +6i(√(3/5))−1=0 (9/(25))+10×−(3/5)×(√((3/5) ))i +6i(√(3/5))−1=0 (9/(25))−6i(√((3/5) ))+6i(√(3/5))−1=0 (9/(25))−1≠0

$$\mathrm{t}^{\mathrm{4}} +\mathrm{10t}^{\mathrm{3}} +\mathrm{6t}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{If}\:\mathrm{one}\:\mathrm{root}\:\mathrm{is}\sqrt{\frac{\mathrm{3}}{\mathrm{5}}\:}{i}\: \\ $$$$\left(\sqrt{\frac{\mathrm{3}}{\mathrm{5}}\:}{i}\:\right)^{\mathrm{4}} +\mathrm{10}\left(\sqrt{\frac{\mathrm{3}}{\mathrm{5}}\:}{i}\:\right)^{\mathrm{3}} +\mathrm{6}\left(\sqrt{\frac{\mathrm{3}}{\mathrm{5}}\:}{i}\:\right)−\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{9}}{\mathrm{25}}+\mathrm{10}\left(\sqrt{\frac{\mathrm{3}}{\mathrm{5}}\:}{i}\:\right)\left(\sqrt{\frac{\mathrm{3}}{\mathrm{5}}\:}{i}\:\right)^{\mathrm{2}} +\mathrm{6i}\sqrt{\frac{\mathrm{3}}{\mathrm{5}}}−\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{9}}{\mathrm{25}}+\mathrm{10}×−\frac{\mathrm{3}}{\mathrm{5}}×\sqrt{\frac{\mathrm{3}}{\mathrm{5}}\:}{i}\:+\mathrm{6i}\sqrt{\frac{\mathrm{3}}{\mathrm{5}}}−\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{9}}{\mathrm{25}}−\mathrm{6i}\sqrt{\frac{\mathrm{3}}{\mathrm{5}}\:}+\mathrm{6i}\sqrt{\frac{\mathrm{3}}{\mathrm{5}}}−\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{9}}{\mathrm{25}}−\mathrm{1}\neq\mathrm{0} \\ $$

Commented by $@ty@m last updated on 28/May/18

$${You}\:{are}\:{right}. \\ $$$${I}'{ll}\:{try}\:{again}. \\ $$$${Thanks}\:{for}\:{correcting}\:{me}. \\ $$

Commented by MJS last updated on 29/May/18

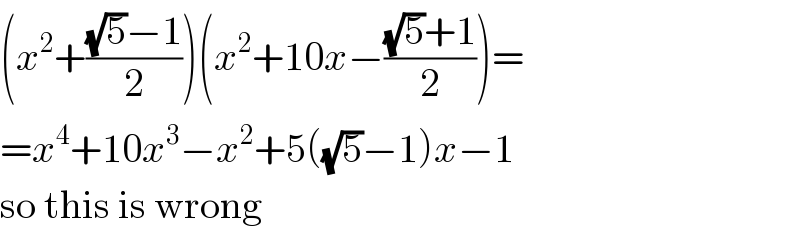
(x^2 +(((√5)−1)/2))(x^2 +10x−(((√5)+1)/2))= =x^4 +10x^3 −x^2 +5((√5)−1)x−1 so this is wrong

$$\left({x}^{\mathrm{2}} +\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\left({x}^{\mathrm{2}} +\mathrm{10}{x}−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)= \\ $$$$={x}^{\mathrm{4}} +\mathrm{10}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{5}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right){x}−\mathrm{1} \\ $$$$\mathrm{so}\:\mathrm{this}\:\mathrm{is}\:\mathrm{wrong} \\ $$

Answered by Rasheed.Sindhi last updated on 28/May/18

..... ........ t^4 +10t^3 +6t−1=0 (Drived by Mr tanmay) ⇒(t^2 +At+B)(t^2 +Ct+D)=0 (Say) Where BD=−1 t^4 +Ct^3 + Dt^2 +At^3 +ACt^2 +ADt + Bt^2 +BCt+BD(=−1)=0 −−−−−−−−−−−−−−−−−− t^4 +(A+C)t^3 +(AC+B+D)t^2 +(AD+BC)t−1=0 A+C=10,AC+B+D=0,AD+BC=6 ( BD=−1 A+C=10 AC+B+D=0 AD+BC=6 are the same equations as in an other question(Q#35892) by Mr behi) It seems that Mr behi has applied above approach and encounterd the above set of equations and he posted it as an other question. Am I right Mr Abu Behi! :) ....

$$….. \\ $$$$…….. \\ $$$$\mathrm{t}^{\mathrm{4}} +\mathrm{10t}^{\mathrm{3}} +\mathrm{6t}−\mathrm{1}=\mathrm{0}\:\left(\mathrm{Drived}\:\mathrm{by}\:\mathrm{Mr}\:\mathrm{tanmay}\right) \\ $$$$\Rightarrow\left(\mathrm{t}^{\mathrm{2}} +\mathrm{At}+\mathrm{B}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{Ct}+\mathrm{D}\right)=\mathrm{0}\:\left(\mathrm{Say}\right) \\ $$$$\:\:\:\:\:\mathrm{Where}\:\mathrm{BD}=−\mathrm{1} \\ $$$$\:\mathrm{t}^{\mathrm{4}} +\mathrm{Ct}^{\mathrm{3}} +\:\:\:\mathrm{Dt}^{\mathrm{2}} \\ $$$$\:\:\:\:\:+\mathrm{At}^{\mathrm{3}} +\mathrm{ACt}^{\mathrm{2}} +\mathrm{ADt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\mathrm{Bt}^{\mathrm{2}} \:+\mathrm{BCt}+\mathrm{BD}\left(=−\mathrm{1}\right)=\mathrm{0} \\ $$$$−−−−−−−−−−−−−−−−−− \\ $$$$\mathrm{t}^{\mathrm{4}} +\left(\mathrm{A}+\mathrm{C}\right)\mathrm{t}^{\mathrm{3}} +\left(\mathrm{AC}+\mathrm{B}+\mathrm{D}\right)\mathrm{t}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{AD}+\mathrm{BC}\right)\mathrm{t}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{A}+\mathrm{C}=\mathrm{10},\mathrm{AC}+\mathrm{B}+\mathrm{D}=\mathrm{0},\mathrm{AD}+\mathrm{BC}=\mathrm{6} \\ $$$$\left(\:\mathrm{BD}=−\mathrm{1}\right. \\ $$$$\mathrm{A}+\mathrm{C}=\mathrm{10} \\ $$$$\mathrm{AC}+\mathrm{B}+\mathrm{D}=\mathrm{0} \\ $$$$\mathrm{AD}+\mathrm{BC}=\mathrm{6} \\ $$$$\mathrm{are}\:\mathrm{the}\:\mathrm{same}\:\mathrm{equations}\:\mathrm{as}\:\mathrm{in}\:\mathrm{an}\:\mathrm{other} \\ $$$$\left.\mathrm{question}\left(\mathrm{Q}#\mathrm{35892}\right)\:\mathrm{by}\:\mathrm{Mr}\:\mathrm{behi}\right) \\ $$$$\mathrm{It}\:\mathrm{seems}\:\mathrm{that}\:\mathrm{Mr}\:\mathrm{behi}\:\mathrm{has}\:\mathrm{applied} \\ $$$$\mathrm{above}\:\mathrm{approach}\:\mathrm{and}\:\mathrm{encounterd} \\ $$$$\mathrm{the}\:\mathrm{above}\:\mathrm{set}\:\mathrm{of}\:\mathrm{equations}\:\mathrm{and}\:\mathrm{he} \\ $$$$\mathrm{posted}\:\mathrm{it}\:\mathrm{as}\:\mathrm{an}\:\mathrm{other}\:\mathrm{question}. \\ $$$$\left.\mathrm{Am}\:\mathrm{I}\:\mathrm{right}\:\mathrm{Mr}\:\mathrm{Abu}\:\mathrm{Behi}!\::\right) \\ $$$$ \\ $$$$…. \\ $$

Commented by behi83417@gmail.com last updated on 28/May/18

$${mr}\:{Rasheed}!{you}\:{are}\:{right}. \\ $$$${but}\:{i}\:{have}\:{not}\:{solution}\:{for}\:{this}\:{and}\: \\ $$$${I}\:{am}\:{waiting}\:{for}\:{my}\:{friends}\:{such}\:{as} \\ $$$${you}\:{and}\:{mr}\:{tanmay}\:{and}\:{mr}\:{satyam}..! \\ $$

Commented by Rasheed.Sindhi last updated on 28/May/18

Mr Abu Behi You don′t know the solution but at least you know how to factorize the following: x^4 +10x^3 +6x−1 =(x^2 +(((√5)−1)/2))(x^2 +10x−(((√5)+1)/2)) −−−−−−−−−−−−−−− (x^2 +(((√5)−1)/2))(x^2 +10x−(((√5)+1)/2))=0 ⇒x^2 =−(((√5)−1)/2)<0⇒ x is not real Or ⇒x=((−10±(√(100+2(√5)+2)))/2) tan((θ/2)) =((−10±(√(100+2(√5)+2)))/2) (θ/2)=tan^(−1) (((−10±(√(100+2(√5)+2)))/2)) θ=2tan^(−1) (((−10±(√(100+2(√5)+2)))/2)) θ=18.10° , −168.76° (out of permited range) θ=18.10° =0.31588 rad

$$\mathrm{Mr}\:\mathrm{Abu}\:\mathrm{Behi} \\ $$$$\:\mathrm{You}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{but}\:\mathrm{at}\:\mathrm{least} \\ $$$$\:\mathrm{you}\:\mathrm{know}\:\mathrm{how}\:\mathrm{to}\:\mathrm{factorize}\:\mathrm{the}\:\mathrm{following}: \\ $$$${x}^{\mathrm{4}} +\mathrm{10}{x}^{\mathrm{3}} +\mathrm{6}{x}−\mathrm{1} \\ $$$$=\left({x}^{\mathrm{2}} +\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\left({x}^{\mathrm{2}} +\mathrm{10}{x}−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\:\:\:\left({x}^{\mathrm{2}} +\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)\left({x}^{\mathrm{2}} +\mathrm{10}{x}−\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =−\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}<\mathrm{0}\Rightarrow\:{x}\:\mathrm{is}\:\mathrm{not}\:\mathrm{real} \\ $$$$\mathrm{Or} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{10}\pm\sqrt{\mathrm{100}+\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{2}}}{\mathrm{2}} \\ $$$$\mathrm{tan}\left(\frac{\theta}{\mathrm{2}}\right)\:=\frac{−\mathrm{10}\pm\sqrt{\mathrm{100}+\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{2}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\frac{\theta}{\mathrm{2}}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{−\mathrm{10}\pm\sqrt{\mathrm{100}+\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\theta=\mathrm{2tan}^{−\mathrm{1}} \left(\frac{−\mathrm{10}\pm\sqrt{\mathrm{100}+\mathrm{2}\sqrt{\mathrm{5}}+\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$\:\theta=\mathrm{18}.\mathrm{10}°\:,\:−\mathrm{168}.\mathrm{76}°\:\left(\mathrm{out}\:\mathrm{of}\:\mathrm{permited}\:\mathrm{range}\right) \\ $$$$\theta=\mathrm{18}.\mathrm{10}°\:=\mathrm{0}.\mathrm{31588}\:\mathrm{rad} \\ $$

Commented by behi83417@gmail.com last updated on 31/May/18

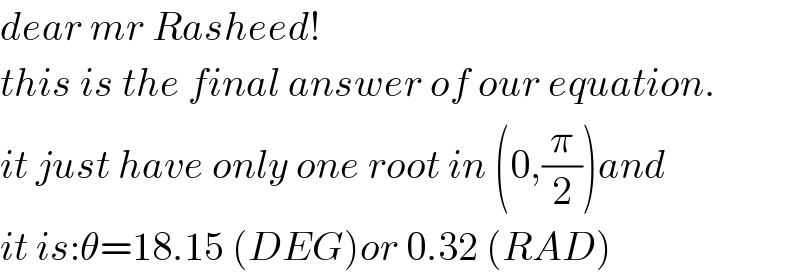
dear mr Rasheed! this is the final answer of our equation. it just have only one root in (0,(π/2))and it is:θ=18.15 (DEG)or 0.32 (RAD)

$${dear}\:{mr}\:{Rasheed}! \\ $$$${this}\:{is}\:{the}\:{final}\:{answer}\:{of}\:{our}\:{equation}. \\ $$$${it}\:{just}\:{have}\:{only}\:{one}\:{root}\:{in}\:\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right){and} \\ $$$${it}\:{is}:\theta=\mathrm{18}.\mathrm{15}\:\left({DEG}\right){or}\:\mathrm{0}.\mathrm{32}\:\left({RAD}\right) \\ $$

Answered by Rasheed.Sindhi last updated on 28/May/18

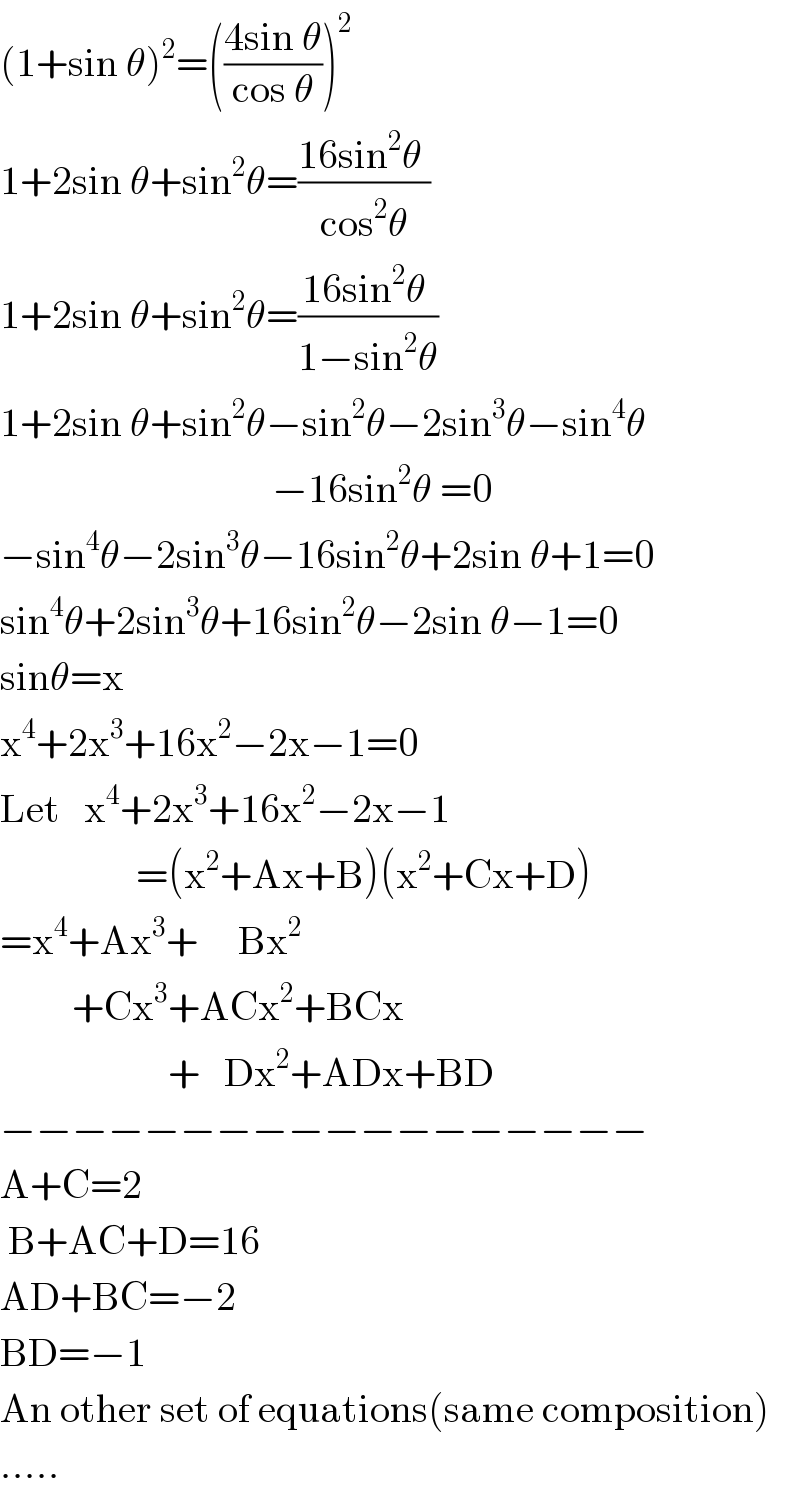
(1+sin θ)^2 =(((4sin θ)/(cos θ)))^2 1+2sin θ+sin^2 θ=((16sin^2 θ )/(cos^2 θ)) 1+2sin θ+sin^2 θ=((16sin^2 θ )/(1−sin^2 θ)) 1+2sin θ+sin^2 θ−sin^2 θ−2sin^3 θ−sin^4 θ −16sin^2 θ =0 −sin^4 θ−2sin^3 θ−16sin^2 θ+2sin θ+1=0 sin^4 θ+2sin^3 θ+16sin^2 θ−2sin θ−1=0 sinθ=x x^4 +2x^3 +16x^2 −2x−1=0 Let x^4 +2x^3 +16x^2 −2x−1 =(x^2 +Ax+B)(x^2 +Cx+D) =x^4 +Ax^3 + Bx^2 +Cx^3 +ACx^2 +BCx + Dx^2 +ADx+BD −−−−−−−−−−−−−−−−−− A+C=2 B+AC+D=16 AD+BC=−2 BD=−1 An other set of equations(same composition) .....

$$\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} =\left(\frac{\mathrm{4sin}\:\theta}{\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{2sin}\:\theta+\mathrm{sin}^{\mathrm{2}} \theta=\frac{\mathrm{16sin}^{\mathrm{2}} \theta\:}{\mathrm{cos}^{\mathrm{2}} \theta}\: \\ $$$$\mathrm{1}+\mathrm{2sin}\:\theta+\mathrm{sin}^{\mathrm{2}} \theta=\frac{\mathrm{16sin}^{\mathrm{2}} \theta\:}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta}\: \\ $$$$\mathrm{1}+\mathrm{2sin}\:\theta+\mathrm{sin}^{\mathrm{2}} \theta−\mathrm{sin}^{\mathrm{2}} \theta−\mathrm{2sin}^{\mathrm{3}} \theta−\mathrm{sin}^{\mathrm{4}} \theta\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{16sin}^{\mathrm{2}} \theta\:=\mathrm{0} \\ $$$$−\mathrm{sin}^{\mathrm{4}} \theta−\mathrm{2sin}^{\mathrm{3}} \theta−\mathrm{16sin}^{\mathrm{2}} \theta+\mathrm{2sin}\:\theta+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{2sin}^{\mathrm{3}} \theta+\mathrm{16sin}^{\mathrm{2}} \theta−\mathrm{2sin}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{sin}\theta=\mathrm{x} \\ $$$$\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{16x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{Let}\:\:\:\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{16x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{Ax}+\mathrm{B}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{Cx}+\mathrm{D}\right) \\ $$$$=\mathrm{x}^{\mathrm{4}} +\mathrm{Ax}^{\mathrm{3}} +\:\:\:\:\:\mathrm{Bx}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:+\mathrm{Cx}^{\mathrm{3}} +\mathrm{ACx}^{\mathrm{2}} +\mathrm{BCx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\mathrm{Dx}^{\mathrm{2}} +\mathrm{ADx}+\mathrm{BD} \\ $$$$−−−−−−−−−−−−−−−−−− \\ $$$$\mathrm{A}+\mathrm{C}=\mathrm{2}\: \\ $$$$\:\mathrm{B}+\mathrm{AC}+\mathrm{D}=\mathrm{16}\: \\ $$$$\mathrm{AD}+\mathrm{BC}=−\mathrm{2} \\ $$$$\mathrm{BD}=−\mathrm{1} \\ $$$$\mathrm{An}\:\mathrm{other}\:\mathrm{set}\:\mathrm{of}\:\mathrm{equations}\left(\mathrm{same}\:\mathrm{composition}\right) \\ $$$$….. \\ $$

Commented by behi83417@gmail.com last updated on 28/May/18

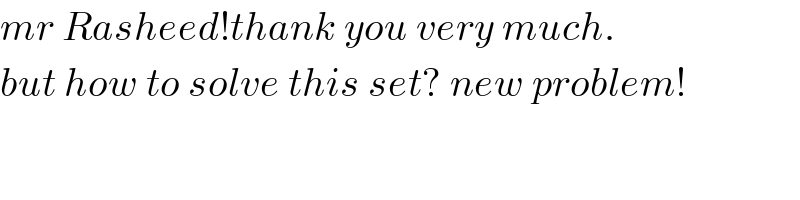
$${mr}\:{Rasheed}!{thank}\:{you}\:{very}\:{much}. \\ $$$${but}\:{how}\:{to}\:{solve}\:{this}\:{set}?\:{new}\:{problem}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply