Menu Close

Question-35851

Tinku Tara 0 Comments
Pin




Question Number 35851 by ajfour last updated on 24/May/18
Commented by ajfour last updated on 25/May/18
Q.35828 continuation.. Find electric potential at point P(x_0 ,y_0 ,z_0 ) due to the charged square wire frame.
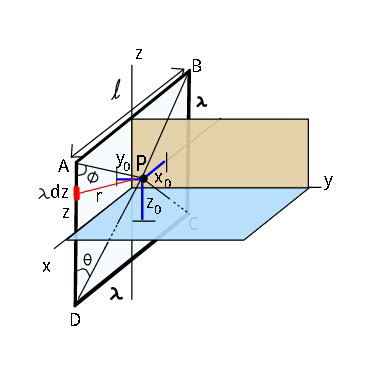
$${Q}.\mathrm{35828}\:{continuation}.. \\ $$$${Find}\:{electric}\:{potential}\:{at}\:{point}\: \\ $$$${P}\left({x}_{\mathrm{0}} ,{y}_{\mathrm{0}} ,{z}_{\mathrm{0}} \right)\:{due}\:{to}\:{the}\:{charged} \\ $$$${square}\:{wire}\:{frame}. \\ $$
Answered by ajfour last updated on 25/May/18
Potential at P(x_0 ,y_0 ,z_0 ) due to line charge AD is dV=((λdz)/(4πε_0 r)) = ((λdz)/(4πε_0 (√(((l/2)−x_0 )^2 +y_0 ^2 +(z−z_0 )^2 )))) let p_⊥ ^2 =((l/2)−x_0 )^2 +y_0 ^2 ∫dV _(AD) = (λ/(4πε_0 ))∫_(−l/2) ^( l/2) (dz/( (√(p_⊥ ^2 +(z−z_0 )^2 )))) V_(AD) =(λ/(4πε_0 ))ln ((((l/2)−z_0 +(√(p_⊥ ^2 +((l/2)−z_0 )^2 )))/(−(l/2)−z_0 +(√(p_⊥ ^2 +((l/2)+z_0 )^2 ))))) similarly V_(BC) = (λ/(4πε_0 ))∫_(−l/2) ^( l/2) (dz/( (√((x_0 +(l/2))^2 +y_0 ^2 +(z−z_0 )^2 )))) let q_⊥ ^2 =(x_0 +(l/2))^2 +y_0 ^2 V_(BC) =(λ/(4πε_0 ))ln ((((l/2)−z_0 +(√(q_⊥ ^2 +((l/2)−z_0 )^2 )))/(−(l/2)−z_0 +(√(q_⊥ ^2 +((l/2)+z_0 )^2 ))))) similarly V_(AB) and V_(CD) . V_P = V_(AB) +V_(BC) +V_(CD) +V_(AD) .
$${Potential}\:{at}\:{P}\left({x}_{\mathrm{0}} ,{y}_{\mathrm{0}} ,{z}_{\mathrm{0}} \right)\:{due}\:{to} \\ $$$${line}\:{charge}\:{AD}\:{is} \\ $$$$\:\:\:\:\:{dV}=\frac{\lambda{dz}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {r}}\:=\:\frac{\lambda{dz}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} \sqrt{\left(\frac{{l}}{\mathrm{2}}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} +{y}_{\mathrm{0}} ^{\mathrm{2}} +\left({z}−{z}_{\mathrm{0}} \right)^{\mathrm{2}} }} \\ $$$${let}\:\:{p}_{\bot} ^{\mathrm{2}} =\left(\frac{{l}}{\mathrm{2}}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} +{y}_{\mathrm{0}} ^{\mathrm{2}} \: \\ $$$$\int{dV}\:_{{AD}} =\:\frac{\lambda}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{−{l}/\mathrm{2}} ^{\:\:{l}/\mathrm{2}} \frac{{dz}}{\:\sqrt{{p}_{\bot} ^{\mathrm{2}} +\left({z}−{z}_{\mathrm{0}} \right)^{\mathrm{2}} }} \\ $$$${V}_{{AD}} \:=\frac{\lambda}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\mathrm{ln}\:\left(\frac{\frac{{l}}{\mathrm{2}}−{z}_{\mathrm{0}} +\sqrt{{p}_{\bot} ^{\mathrm{2}} +\left(\frac{{l}}{\mathrm{2}}−{z}_{\mathrm{0}} \right)^{\mathrm{2}} }}{−\frac{{l}}{\mathrm{2}}−{z}_{\mathrm{0}} +\sqrt{{p}_{\bot} ^{\mathrm{2}} +\left(\frac{{l}}{\mathrm{2}}+{z}_{\mathrm{0}} \right)^{\mathrm{2}} }}\right) \\ $$$$\:\:{similarly} \\ $$$${V}_{{BC}} \:\:=\:\frac{\lambda}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{−{l}/\mathrm{2}} ^{\:\:{l}/\mathrm{2}} \frac{{dz}}{\:\sqrt{\left({x}_{\mathrm{0}} +\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}_{\mathrm{0}} ^{\mathrm{2}} +\left({z}−{z}_{\mathrm{0}} \right)^{\mathrm{2}} }} \\ $$$${let}\:{q}_{\bot} ^{\mathrm{2}} =\left({x}_{\mathrm{0}} +\frac{{l}}{\mathrm{2}}\right)^{\mathrm{2}} +{y}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$${V}_{{BC}} \:=\frac{\lambda}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\mathrm{ln}\:\left(\frac{\frac{{l}}{\mathrm{2}}−{z}_{\mathrm{0}} +\sqrt{{q}_{\bot} ^{\mathrm{2}} +\left(\frac{{l}}{\mathrm{2}}−{z}_{\mathrm{0}} \right)^{\mathrm{2}} }}{−\frac{{l}}{\mathrm{2}}−{z}_{\mathrm{0}} +\sqrt{{q}_{\bot} ^{\mathrm{2}} +\left(\frac{{l}}{\mathrm{2}}+{z}_{\mathrm{0}} \right)^{\mathrm{2}} }}\right) \\ $$$${similarly}\:{V}_{{AB}} \:\:{and}\:\:{V}_{{CD}} \:. \\ $$$${V}_{{P}} \:=\:{V}_{{AB}} +{V}_{{BC}} +{V}_{{CD}} +{V}_{{AD}} \:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *