Menu Close

Question-35872

Tinku Tara 0 Comments
Pin




Question Number 35872 by Rasheed.Sindhi last updated on 25/May/18
Commented by Tinkutara last updated on 25/May/18
Yes this was also my doubt!
Answered by Rasheed.Sindhi last updated on 26/May/18
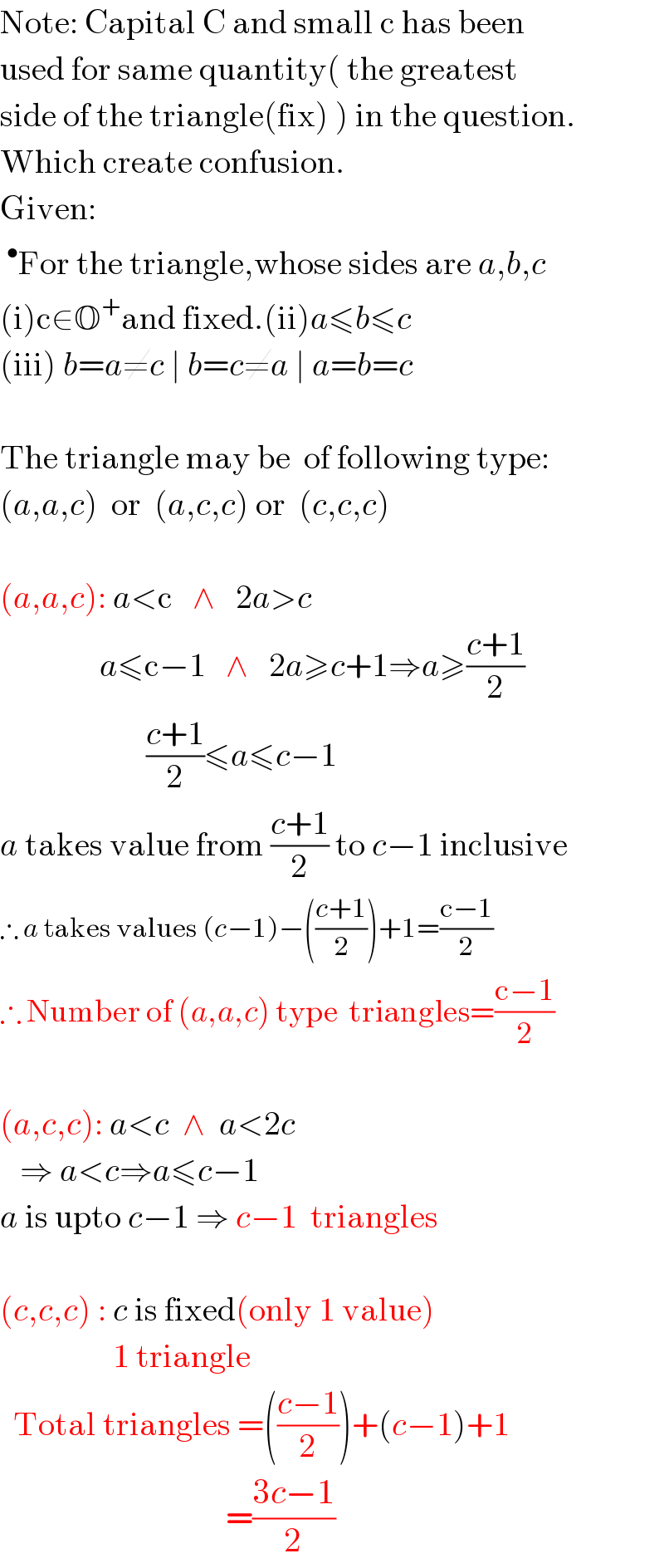
Note: Capital C and small c has been used for same quantity( the greatest side of the triangle(fix) ) in the question. Which create confusion. Given: ^• For the triangle,whose sides are a,b,c (i)c∈O^+ and fixed.(ii)a≤b≤c (iii) b=a≠c ∣ b=c≠a ∣ a=b=c The triangle may be of following type: (a,a,c) or (a,c,c) or (c,c,c) (a,a,c): a<c ∧ 2a>c a≤c−1 ∧ 2a≥c+1⇒a≥((c+1)/2) ((c+1)/2)≤a≤c−1 a takes value from ((c+1)/2) to c−1 inclusive ∴ a takes values (c−1)−(((c+1)/2))+1=((c−1)/2) ∴ Number of (a,a,c) type triangles=((c−1)/2) (a,c,c): a<c ∧ a<2c ⇒ a<c⇒a≤c−1 a is upto c−1 ⇒ c−1 triangles (c,c,c) : c is fixed(only 1 value) 1 triangle Total triangles =(((c−1)/2))+(c−1)+1 =((3c−1)/2)
$$\mathrm{Note}:\:\mathrm{Capital}\:\mathrm{C}\:\mathrm{and}\:\mathrm{small}\:\mathrm{c}\:\mathrm{has}\:\mathrm{been} \\ $$$$\mathrm{used}\:\mathrm{for}\:\mathrm{same}\:\mathrm{quantity}\left(\:\mathrm{the}\:\mathrm{greatest}\right. \\ $$$$\left.\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\left(\mathrm{fix}\right)\:\right)\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}. \\ $$$$\mathrm{Which}\:\mathrm{create}\:\mathrm{confusion}. \\ $$$$\mathrm{Given}: \\ $$$$\:^{\bullet} \mathrm{For}\:\mathrm{the}\:\mathrm{triangle},\mathrm{whose}\:\mathrm{sides}\:\mathrm{are}\:{a},{b},{c} \\ $$$$\left(\mathrm{i}\right)\mathrm{c}\in\mathbb{O}^{+} \mathrm{and}\:\mathrm{fixed}.\left(\mathrm{ii}\right){a}\leqslant{b}\leqslant{c} \\ $$$$\left(\mathrm{iii}\right)\:{b}={a}\neq{c}\:\mid\:{b}={c}\neq{a}\:\mid\:{a}={b}={c} \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{triangle}\:\mathrm{may}\:\mathrm{be}\:\:\mathrm{of}\:\mathrm{following}\:\mathrm{type}: \\ $$$$\left({a},{a},{c}\right)\:\:\mathrm{or}\:\:\left({a},{c},{c}\right)\:\mathrm{or}\:\:\left({c},{c},{c}\right) \\ $$$$ \\ $$$$\left({a},{a},{c}\right):\:{a}<\mathrm{c}\:\:\:\wedge\:\:\:\mathrm{2}{a}>{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}\leqslant\mathrm{c}−\mathrm{1}\:\:\:\wedge\:\:\:\mathrm{2}{a}\geqslant{c}+\mathrm{1}\Rightarrow{a}\geqslant\frac{{c}+\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{c}+\mathrm{1}}{\mathrm{2}}\leqslant{a}\leqslant{c}−\mathrm{1} \\ $$$${a}\:\mathrm{takes}\:\mathrm{value}\:\mathrm{from}\:\frac{{c}+\mathrm{1}}{\mathrm{2}}\:\mathrm{to}\:{c}−\mathrm{1}\:\mathrm{inclusive} \\ $$$$\therefore\:{a}\:\mathrm{takes}\:\mathrm{values}\:\left({c}−\mathrm{1}\right)−\left(\frac{{c}+\mathrm{1}}{\mathrm{2}}\right)+\mathrm{1}=\frac{\mathrm{c}−\mathrm{1}}{\mathrm{2}} \\ $$$$\therefore\:\mathrm{Number}\:\mathrm{of}\:\left({a},{a},{c}\right)\:\mathrm{type}\:\:\mathrm{triangles}=\frac{\mathrm{c}−\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\left({a},{c},{c}\right):\:{a}<{c}\:\:\wedge\:\:{a}<\mathrm{2}{c} \\ $$$$\:\:\:\Rightarrow\:{a}<{c}\Rightarrow{a}\leqslant{c}−\mathrm{1} \\ $$$${a}\:\mathrm{is}\:\mathrm{upto}\:{c}−\mathrm{1}\:\Rightarrow\:{c}−\mathrm{1}\:\:\mathrm{triangles} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\left({c},{c},{c}\right)\::\:{c}\:\mathrm{is}\:\mathrm{fixed}\left(\mathrm{only}\:\mathrm{1}\:\mathrm{value}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\mathrm{triangle} \\ $$$$\:\:\mathrm{Total}\:\mathrm{triangles}\:=\left(\frac{{c}−\mathrm{1}}{\mathrm{2}}\right)+\left({c}−\mathrm{1}\right)+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}{c}−\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Tinkutara last updated on 26/May/18
Thanks Sir!
Commented by Rasheed.Sindhi last updated on 26/May/18
Could you tell me the name and author of the book,which contains so much interesting questions?Is there its soft copy on the net?
$$\mathrm{Could}\:\mathrm{you}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{the}\:\mathrm{name}\:\mathrm{and}\:\mathrm{author} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{book},\mathrm{which}\:\mathrm{contains}\:\mathrm{so}\:\mathrm{much} \\ $$$$\mathrm{interesting}\:\mathrm{questions}?\mathrm{Is}\:\mathrm{there}\:\mathrm{its}\:\mathrm{soft} \\ $$$$\mathrm{copy}\:\mathrm{on}\:\mathrm{the}\:\mathrm{net}? \\ $$
Commented by Tinkutara last updated on 26/May/18
It is just a coaching material and not any standard book �� And not all the questions are interesting, being some too easy while some too hard ��
Commented by Rasheed.Sindhi last updated on 26/May/18
�� Anyway sir, we received some interesting questions of it through you!
Commented by Rasheed.Sindhi last updated on 26/May/18
You mentioned about the question: "Yes this was also my doubt!" What was that doubt?
Commented by Tinkutara last updated on 26/May/18
The question.
$${The}\:{question}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *