Menu Close

Question-35892

Tinku Tara 0 Comments
Pin




Question Number 35892 by behi83417@gmail.com last updated on 25/May/18
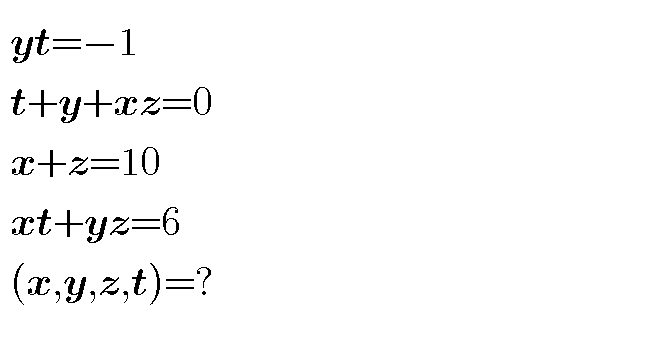
Commented by tanmay.chaudhury50@gmail.com last updated on 26/May/18
i am very near to find the answer...its a very good problem...
$${i}\:{am}\:{very}\:{near}\:{to}\:{find}\:{the}\:{answer}…{its}\:{a}\:{very}\:{good} \\ $$$${problem}… \\ $$
Commented by Rasheed.Sindhi last updated on 29/May/18
We′re waiting for your answer sir.
$$\mathrm{We}'\mathrm{re}\:\mathrm{waiting}\:\mathrm{for}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/May/18
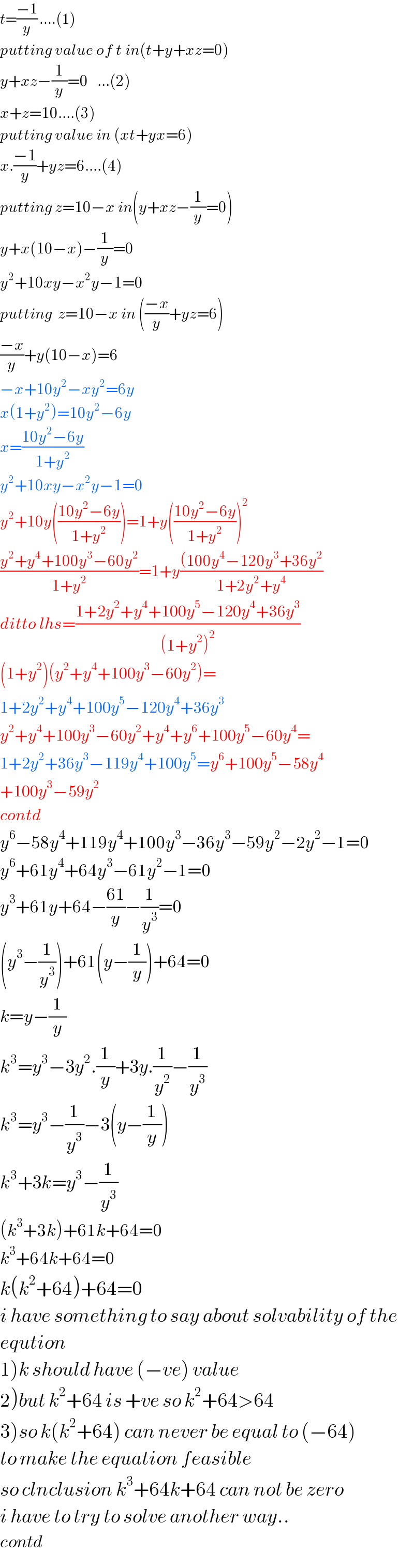
t=((−1)/y) ....(1) putting value of t in(t+y+xz=0) y+xz−(1/y)=0 ...(2) x+z=10....(3) putting value in (xt+yx=6) x.((−1)/y)+yz=6....(4) putting z=10−x in(y+xz−(1/y)=0) y+x(10−x)−(1/y)=0 y^2 +10xy−x^2 y−1=0 putting z=10−x in (((−x)/y)+yz=6) ((−x)/y)+y(10−x)=6 −x+10y^2 −xy^2 =6y x(1+y^2 )=10y^2 −6y x=((10y^2 −6y)/(1+y^2 )) y^2 +10xy−x^2 y−1=0 y^2 +10y(((10y^2 −6y)/(1+y^2 )))=1+y(((10y^2 −6y)/(1+y^2 )))^2 ((y^2 +y^4 +100y^3 −60y^2 )/(1+y^2 ))=1+y(((100y^4 −120y^3 +36y^2 )/(1+2y^2 +y^4 )) ditto lhs=((1+2y^2 +y^4 +100y^5 −120y^4 +36y^3 )/((1+y^2 )^2 )) (1+y_ ^2 )(y^2 +y^4 +100y^3 −60y^2 )= 1+2y^2 +y^4 +100y^5 −120y^4 +36y^3 y^2 +y^4 +100y^3 −60y^2 +y^4 +y^6 +100y^5 −60y^4 = 1+2y^2 +36y^3 −119y^4 +100y^5 =y^6 +100y^5 −58y^4 +100y^3 −59y^2 contd y^6 −58y^4 +119y^4 +100y^3 −36y^3 −59y^2 −2y^2 −1=0 y^6 +61y^4 +64y^3 −61y^2 −1=0 y^3 +61y+64−((61)/y)−(1/y^3 )=0 (y^3 −(1/y^3 ))+61(y−(1/y))+64=0 k=y−(1/y) k^3 =y^3 −3y^2 .(1/y)+3y.(1/y^2 )−(1/y^3 ) k^3 =y^3 −(1/y^3 )−3(y−(1/y)) k^3 +3k=y^3 −(1/y^3 ) (k^3 +3k)+61k+64=0 k^3 +64k+64=0 k(k^2 +64)+64=0 i have something to say about solvability of the eqution 1)k should have (−ve) value 2)but k^2 +64 is +ve so k^2 +64>64 3)so k(k^2 +64) can never be equal to (−64) to make the equation feasible so clnclusion k^3 +64k+64 can not be zero i have to try to solve another way.. contd
$${t}=\frac{−\mathrm{1}}{{y}}\:….\left(\mathrm{1}\right) \\ $$$${putting}\:{value}\:{of}\:{t}\:{in}\left({t}+{y}+{xz}=\mathrm{0}\right) \\ $$$${y}+{xz}−\frac{\mathrm{1}}{{y}}=\mathrm{0}\:\:\:…\left(\mathrm{2}\right) \\ $$$${x}+{z}=\mathrm{10}….\left(\mathrm{3}\right) \\ $$$${putting}\:{value}\:{in}\:\left({xt}+{yx}=\mathrm{6}\right) \\ $$$${x}.\frac{−\mathrm{1}}{{y}}+{yz}=\mathrm{6}….\left(\mathrm{4}\right) \\ $$$${putting}\:{z}=\mathrm{10}−{x}\:{in}\left({y}+{xz}−\frac{\mathrm{1}}{{y}}=\mathrm{0}\right) \\ $$$${y}+{x}\left(\mathrm{10}−{x}\right)−\frac{\mathrm{1}}{{y}}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} +\mathrm{10}{xy}−{x}^{\mathrm{2}} {y}−\mathrm{1}=\mathrm{0} \\ $$$${putting}\:\:{z}=\mathrm{10}−{x}\:{in}\:\left(\frac{−{x}}{{y}}+{yz}=\mathrm{6}\right) \\ $$$$\frac{−{x}}{{y}}+{y}\left(\mathrm{10}−{x}\right)=\mathrm{6} \\ $$$$−{x}+\mathrm{10}{y}^{\mathrm{2}} −{xy}^{\mathrm{2}} =\mathrm{6}{y} \\ $$$${x}\left(\mathrm{1}+{y}^{\mathrm{2}} \right)=\mathrm{10}{y}^{\mathrm{2}} −\mathrm{6}{y} \\ $$$${x}=\frac{\mathrm{10}{y}^{\mathrm{2}} −\mathrm{6}{y}}{\mathrm{1}+{y}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} +\mathrm{10}{xy}−{x}^{\mathrm{2}} {y}−\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} +\mathrm{10}{y}\left(\frac{\mathrm{10}{y}^{\mathrm{2}} −\mathrm{6}{y}}{\mathrm{1}+{y}^{\mathrm{2}} }\right)=\mathrm{1}+{y}\left(\frac{\mathrm{10}{y}^{\mathrm{2}} −\mathrm{6}{y}}{\mathrm{1}+{y}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\frac{{y}^{\mathrm{2}} +{y}^{\mathrm{4}} +\mathrm{100}{y}^{\mathrm{3}} −\mathrm{60}{y}^{\mathrm{2}} }{\mathrm{1}+{y}^{\mathrm{2}} }=\mathrm{1}+{y}\frac{\left(\mathrm{100}{y}^{\mathrm{4}} −\mathrm{120}{y}^{\mathrm{3}} +\mathrm{36}{y}^{\mathrm{2}} \right.}{\mathrm{1}+\mathrm{2}{y}^{\mathrm{2}} +{y}^{\mathrm{4}} } \\ $$$${ditto}\:{lhs}=\frac{\mathrm{1}+\mathrm{2}{y}^{\mathrm{2}} +{y}^{\mathrm{4}} +\mathrm{100}{y}^{\mathrm{5}} −\mathrm{120}{y}^{\mathrm{4}} +\mathrm{36}{y}^{\mathrm{3}} }{\left(\mathrm{1}+{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{1}+{y}_{} ^{\mathrm{2}} \right)\left({y}^{\mathrm{2}} +{y}^{\mathrm{4}} +\mathrm{100}{y}^{\mathrm{3}} −\mathrm{60}{y}^{\mathrm{2}} \right)= \\ $$$$\mathrm{1}+\mathrm{2}{y}^{\mathrm{2}} +{y}^{\mathrm{4}} +\mathrm{100}{y}^{\mathrm{5}} −\mathrm{120}{y}^{\mathrm{4}} +\mathrm{36}{y}^{\mathrm{3}} \\ $$$${y}^{\mathrm{2}} +{y}^{\mathrm{4}} +\mathrm{100}{y}^{\mathrm{3}} −\mathrm{60}{y}^{\mathrm{2}} +{y}^{\mathrm{4}} +{y}^{\mathrm{6}} +\mathrm{100}{y}^{\mathrm{5}} −\mathrm{60}{y}^{\mathrm{4}} = \\ $$$$\mathrm{1}+\mathrm{2}{y}^{\mathrm{2}} +\mathrm{36}{y}^{\mathrm{3}} −\mathrm{119}{y}^{\mathrm{4}} +\mathrm{100}{y}^{\mathrm{5}} ={y}^{\mathrm{6}} +\mathrm{100}{y}^{\mathrm{5}} −\mathrm{58}{y}^{\mathrm{4}} \\ $$$$+\mathrm{100}{y}^{\mathrm{3}} −\mathrm{59}{y}^{\mathrm{2}} \\ $$$${contd} \\ $$$${y}^{\mathrm{6}} −\mathrm{58}{y}^{\mathrm{4}} +\mathrm{119}{y}^{\mathrm{4}} +\mathrm{100}{y}^{\mathrm{3}} −\mathrm{36}{y}^{\mathrm{3}} −\mathrm{59}{y}^{\mathrm{2}} −\mathrm{2}{y}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{6}} +\mathrm{61}{y}^{\mathrm{4}} +\mathrm{64}{y}^{\mathrm{3}} −\mathrm{61}{y}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${y}^{\mathrm{3}} +\mathrm{61}{y}+\mathrm{64}−\frac{\mathrm{61}}{{y}}−\frac{\mathrm{1}}{{y}^{\mathrm{3}} }=\mathrm{0} \\ $$$$\left({y}^{\mathrm{3}} −\frac{\mathrm{1}}{{y}^{\mathrm{3}} }\right)+\mathrm{61}\left({y}−\frac{\mathrm{1}}{{y}}\right)+\mathrm{64}=\mathrm{0} \\ $$$${k}={y}−\frac{\mathrm{1}}{{y}}\:\: \\ $$$${k}^{\mathrm{3}} ={y}^{\mathrm{3}} −\mathrm{3}{y}^{\mathrm{2}} .\frac{\mathrm{1}}{{y}}+\mathrm{3}{y}.\frac{\mathrm{1}}{{y}^{\mathrm{2}} }−\frac{\mathrm{1}}{{y}^{\mathrm{3}} } \\ $$$${k}^{\mathrm{3}} ={y}^{\mathrm{3}} −\frac{\mathrm{1}}{{y}^{\mathrm{3}} }−\mathrm{3}\left({y}−\frac{\mathrm{1}}{{y}}\right) \\ $$$${k}^{\mathrm{3}} +\mathrm{3}{k}={y}^{\mathrm{3}} −\frac{\mathrm{1}}{{y}^{\mathrm{3}} } \\ $$$$\left({k}^{\mathrm{3}} +\mathrm{3}{k}\right)+\mathrm{61}{k}+\mathrm{64}=\mathrm{0} \\ $$$${k}^{\mathrm{3}} +\mathrm{64}{k}+\mathrm{64}=\mathrm{0} \\ $$$${k}\left({k}^{\mathrm{2}} +\mathrm{64}\right)+\mathrm{64}=\mathrm{0} \\ $$$${i}\:{have}\:{something}\:{to}\:{say}\:{about}\:{solvability}\:{of}\:{the} \\ $$$${eqution} \\ $$$$\left.\mathrm{1}\right){k}\:{should}\:{have}\:\left(−{ve}\right)\:{value} \\ $$$$\left.\mathrm{2}\right){but}\:{k}^{\mathrm{2}} +\mathrm{64}\:{is}\:+{ve}\:{so}\:{k}^{\mathrm{2}} +\mathrm{64}>\mathrm{64} \\ $$$$\left.\mathrm{3}\right){so}\:{k}\left({k}^{\mathrm{2}} +\mathrm{64}\right)\:{can}\:{never}\:{be}\:{equal}\:{to}\:\left(−\mathrm{64}\right) \\ $$$${to}\:{make}\:{the}\:{equation}\:{feasible} \\ $$$${so}\:{clnclusion}\:{k}^{\mathrm{3}} +\mathrm{64}{k}+\mathrm{64}\:{can}\:{not}\:{be}\:{zero} \\ $$$${i}\:{have}\:{to}\:{try}\:{to}\:{solve}\:{another}\:{way}.. \\ $$$${contd} \\ $$
Commented by behi83417@gmail.com last updated on 26/May/18
thank you very much sir for your working. i am waiting for your final answer.
$${thank}\:{you}\:{very}\:{much}\:{sir}\:{for}\:{your}\:{working}. \\ $$$${i}\:{am}\:{waiting}\:{for}\:{your}\:{final}\:{answer}. \\ $$
Commented by behi83417@gmail.com last updated on 28/May/18
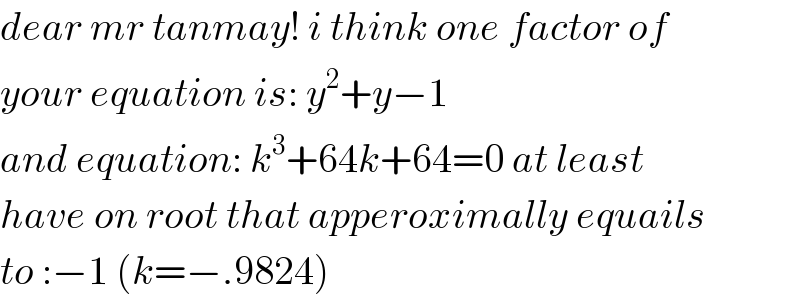
dear mr tanmay! i think one factor of your equation is: y^2 +y−1 and equation: k^3 +64k+64=0 at least have on root that apperoximally equails to :−1 (k=−.9824)
$${dear}\:{mr}\:{tanmay}!\:{i}\:{think}\:{one}\:{factor}\:{of} \\ $$$${your}\:{equation}\:{is}:\:{y}^{\mathrm{2}} +{y}−\mathrm{1} \\ $$$${and}\:{equation}:\:{k}^{\mathrm{3}} +\mathrm{64}{k}+\mathrm{64}=\mathrm{0}\:{at}\:{least} \\ $$$${have}\:{on}\:{root}\:{that}\:{apperoximally}\:{equails} \\ $$$${to}\::−\mathrm{1}\:\left({k}=−.\mathrm{9824}\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/May/18
thanx
$${thanx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/May/18
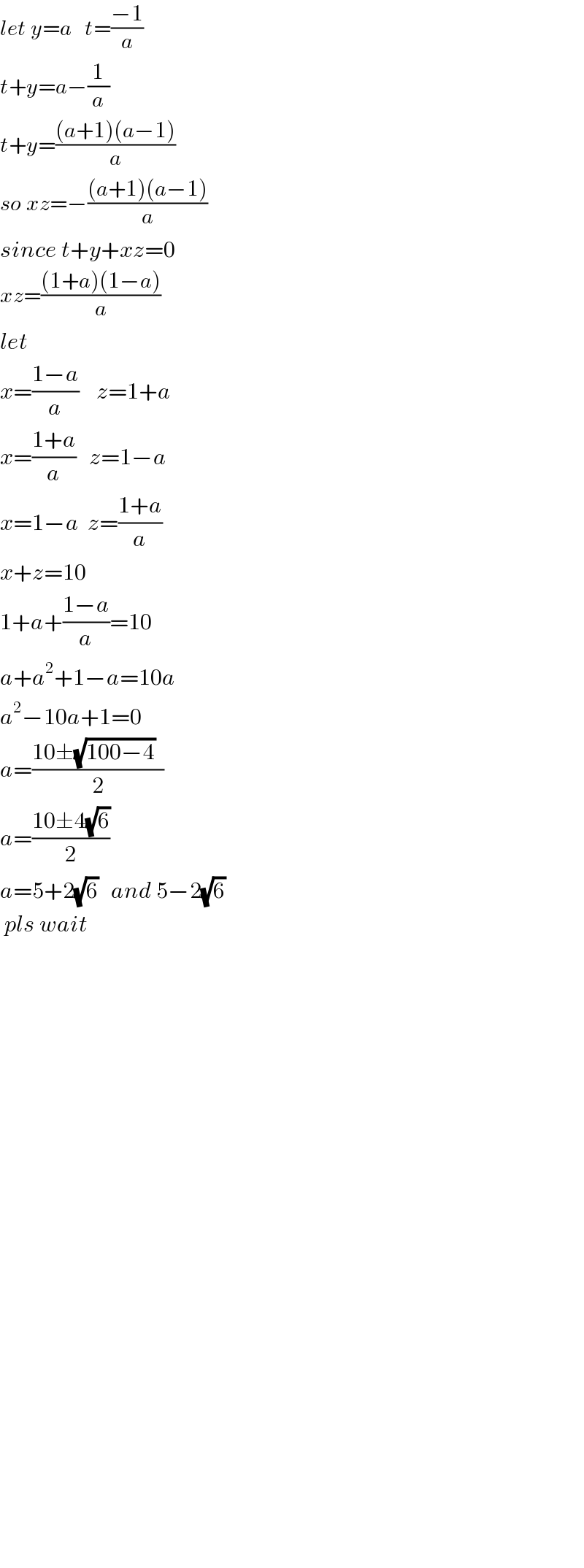
let y=a t=((−1)/a) t+y=a−(1/a) t+y=(((a+1)(a−1))/a) so xz=−(((a+1)(a−1))/a) since t+y+xz=0 xz=(((1+a)(1−a))/a) let x=((1−a)/a) z=1+a x=((1+a)/a) z=1−a x=1−a z=((1+a)/a) x+z=10 1+a+((1−a)/a)=10 a+a^2 +1−a=10a a^2 −10a+1=0 a=((10±(√(100−4)) )/2) a=((10±4(√6))/2) a=5+2(√6) and 5−2(√6) pls wait
$${let}\:{y}={a}\:\:\:{t}=\frac{−\mathrm{1}}{{a}} \\ $$$${t}+{y}={a}−\frac{\mathrm{1}}{{a}} \\ $$$${t}+{y}=\frac{\left({a}+\mathrm{1}\right)\left({a}−\mathrm{1}\right)}{{a}} \\ $$$${so}\:{xz}=−\frac{\left({a}+\mathrm{1}\right)\left({a}−\mathrm{1}\right)}{{a}} \\ $$$${since}\:{t}+{y}+{xz}=\mathrm{0} \\ $$$${xz}=\frac{\left(\mathrm{1}+{a}\right)\left(\mathrm{1}−{a}\right)}{{a}} \\ $$$${let} \\ $$$${x}=\frac{\mathrm{1}−{a}}{{a}}\:\:\:\:{z}=\mathrm{1}+{a} \\ $$$${x}=\frac{\mathrm{1}+{a}}{{a}}\:\:\:{z}=\mathrm{1}−{a} \\ $$$${x}=\mathrm{1}−{a}\:\:{z}=\frac{\mathrm{1}+{a}}{{a}} \\ $$$${x}+{z}=\mathrm{10} \\ $$$$\mathrm{1}+{a}+\frac{\mathrm{1}−{a}}{{a}}=\mathrm{10} \\ $$$${a}+{a}^{\mathrm{2}} +\mathrm{1}−{a}=\mathrm{10}{a} \\ $$$${a}^{\mathrm{2}} −\mathrm{10}{a}+\mathrm{1}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{10}\pm\sqrt{\mathrm{100}−\mathrm{4}}\:\:}{\mathrm{2}} \\ $$$${a}=\frac{\mathrm{10}\pm\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$${a}=\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\:\:\:{and}\:\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\:\: \\ $$$$\:{pls}\:{wait}\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *