Question Number 35968 by RoachDN last updated on 26/May/18

Commented by Joel579 last updated on 26/May/18
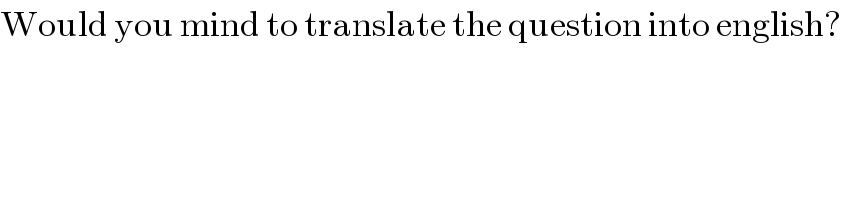
$$\mathrm{Would}\:\mathrm{you}\:\mathrm{mind}\:\mathrm{to}\:\mathrm{translate}\:\mathrm{the}\:\mathrm{question}\:\mathrm{into}\:\mathrm{english}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/May/18
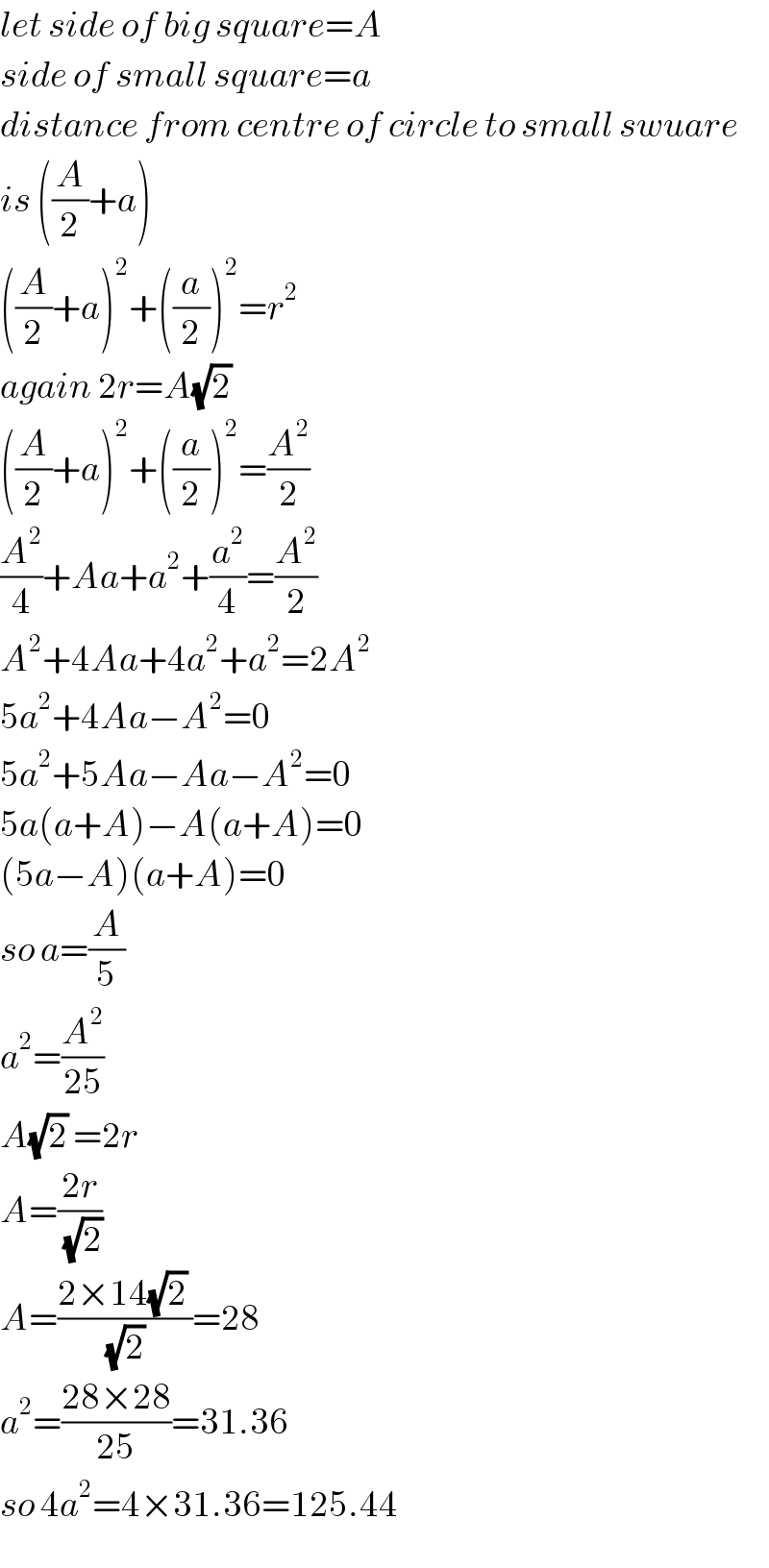
$${let}\:{side}\:{of}\:{big}\:{square}={A} \\ $$$${side}\:{of}\:{small}\:{square}={a} \\ $$$${distance}\:{from}\:{centre}\:{of}\:{circle}\:{to}\:{small}\:{swuare} \\ $$$${is}\:\left(\frac{{A}}{\mathrm{2}}+{a}\right) \\ $$$$\left(\frac{{A}}{\mathrm{2}}+{a}\right)^{\mathrm{2}} +\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${again}\:\mathrm{2}{r}={A}\sqrt{\mathrm{2}}\: \\ $$$$\left(\frac{{A}}{\mathrm{2}}+{a}\right)^{\mathrm{2}} +\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{{A}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{{A}^{\mathrm{2}} }{\mathrm{4}}+{Aa}+{a}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{\mathrm{4}}=\frac{{A}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${A}^{\mathrm{2}} +\mathrm{4}{Aa}+\mathrm{4}{a}^{\mathrm{2}} +{a}^{\mathrm{2}} =\mathrm{2}{A}^{\mathrm{2}} \\ $$$$\mathrm{5}{a}^{\mathrm{2}} +\mathrm{4}{Aa}−{A}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{5}{a}^{\mathrm{2}} +\mathrm{5}{Aa}−{Aa}−{A}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{5}{a}\left({a}+{A}\right)−{A}\left({a}+{A}\right)=\mathrm{0} \\ $$$$\left(\mathrm{5}{a}−{A}\right)\left({a}+{A}\right)=\mathrm{0} \\ $$$${so}\:{a}=\frac{{A}}{\mathrm{5}} \\ $$$${a}^{\mathrm{2}} =\frac{{A}^{\mathrm{2}} }{\mathrm{25}} \\ $$$${A}\sqrt{\mathrm{2}}\:=\mathrm{2}{r} \\ $$$${A}=\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{2}}} \\ $$$${A}=\frac{\mathrm{2}×\mathrm{14}\sqrt{\mathrm{2}}\:}{\:\sqrt{\mathrm{2}}\:}=\mathrm{28} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{28}×\mathrm{28}}{\mathrm{25}}=\mathrm{31}.\mathrm{36} \\ $$$${so}\:\mathrm{4}{a}^{\mathrm{2}} =\mathrm{4}×\mathrm{31}.\mathrm{36}=\mathrm{125}.\mathrm{44} \\ $$
Answered by MJS last updated on 27/May/18
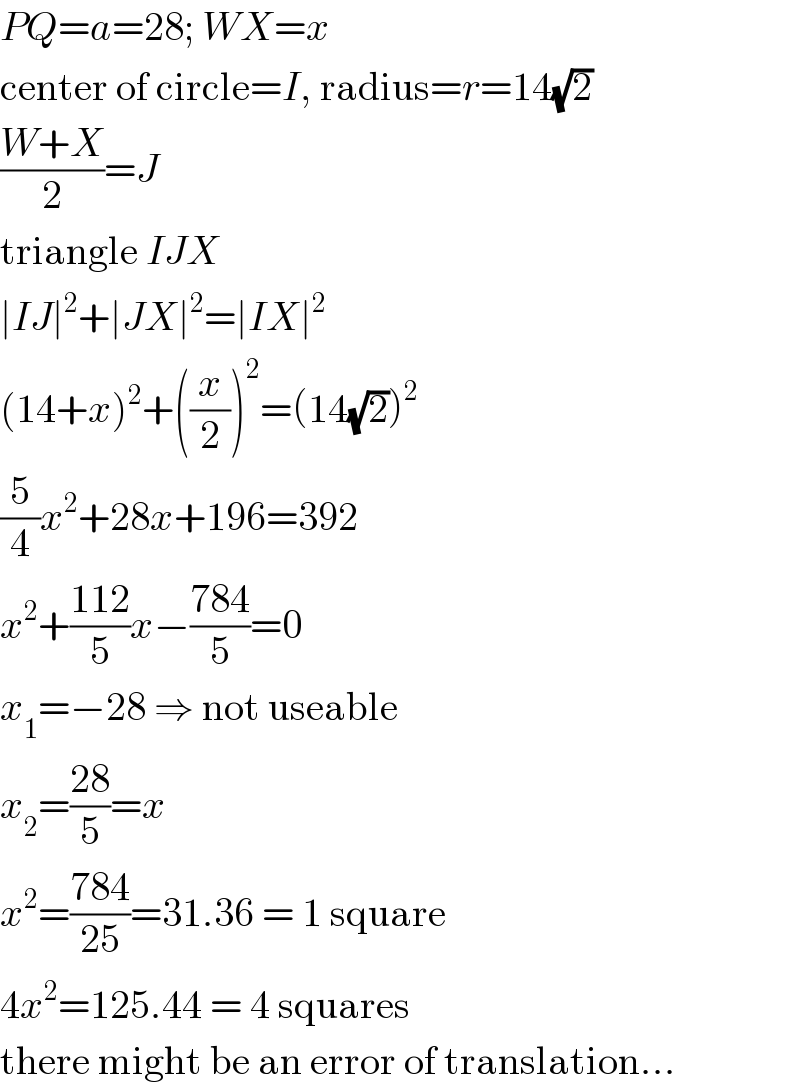
$${PQ}={a}=\mathrm{28};\:{WX}={x} \\ $$$$\mathrm{center}\:\mathrm{of}\:\mathrm{circle}={I},\:\mathrm{radius}={r}=\mathrm{14}\sqrt{\mathrm{2}} \\ $$$$\frac{{W}+{X}}{\mathrm{2}}={J} \\ $$$$\mathrm{triangle}\:{IJX} \\ $$$$\mid{IJ}\mid^{\mathrm{2}} +\mid{JX}\mid^{\mathrm{2}} =\mid{IX}\mid^{\mathrm{2}} \\ $$$$\left(\mathrm{14}+{x}\right)^{\mathrm{2}} +\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\mathrm{14}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{5}}{\mathrm{4}}{x}^{\mathrm{2}} +\mathrm{28}{x}+\mathrm{196}=\mathrm{392} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{112}}{\mathrm{5}}{x}−\frac{\mathrm{784}}{\mathrm{5}}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =−\mathrm{28}\:\Rightarrow\:\mathrm{not}\:\mathrm{useable} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{28}}{\mathrm{5}}={x} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{784}}{\mathrm{25}}=\mathrm{31}.\mathrm{36}\:=\:\mathrm{1}\:\mathrm{square} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} =\mathrm{125}.\mathrm{44}\:=\:\mathrm{4}\:\mathrm{squares} \\ $$$$\mathrm{there}\:\mathrm{might}\:\mathrm{be}\:\mathrm{an}\:\mathrm{error}\:\mathrm{of}\:\mathrm{translation}… \\ $$
