Question Number 36024 by bshahid010@gmail.com last updated on 27/May/18
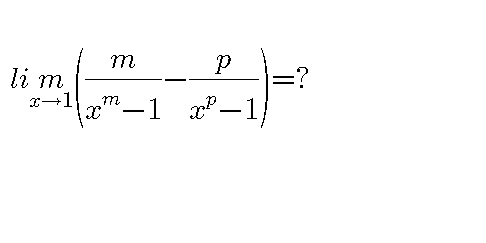
Commented by abdo mathsup 649 cc last updated on 27/May/18

$${let}\:{use}\:{the}\:{changement}\:\:{x}\:=\mathrm{1}+{t}\:{so} \\ $$$$\frac{{m}}{{x}^{{m}} \:−\mathrm{1}}\:−\frac{{p}}{{x}^{{p}} \:−\mathrm{1}}\:=\frac{{m}}{\left(\mathrm{1}+{t}\right)^{{m}} \:−\mathrm{1}}\:−\:\frac{{p}}{\left(\mathrm{1}+{t}\right)^{{p}} \:−\mathrm{1}}\:{but} \\ $$$$\left(\mathrm{1}+{t}\right)^{{m}} \:\sim\:\:\mathrm{1}+{mt}\:+\frac{{m}\left({m}−\mathrm{1}\right)}{\mathrm{2}}\:{t}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{t}\right)^{{p}} \:\sim\:\mathrm{1}+{pt}\:+\frac{{p}\left({p}−\mathrm{1}\right)}{\mathrm{2}}\:{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\frac{{m}}{{x}^{{m}} −\mathrm{1}}\:−\frac{{p}}{{x}^{{p}} −\mathrm{1}}\:\sim\:\:\:\frac{{m}}{{mt}+\frac{{m}\left({m}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} }\:−\frac{{p}}{{pt}\:+\frac{{p}\left({p}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} } \\ $$$$=\:\:\frac{\mathrm{1}}{{t}\:+\frac{{m}−\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{{t}\:+\frac{{p}−\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\left\{\:\:\:\frac{\mathrm{1}}{\mathrm{2}{t}\:+\left({m}−\mathrm{1}\right){t}^{\mathrm{2}} }\:\:−\frac{\mathrm{1}}{\mathrm{2}{t}\:+\left({p}−\mathrm{1}\right){t}^{\mathrm{2}} }\right\} \\ $$$$=\mathrm{2}\left\{\:\frac{\mathrm{2}{t}\:\:+\left({p}−\mathrm{1}\right){t}^{\mathrm{2}} \:−\mathrm{2}{t}\:−\left({m}−\mathrm{1}\right){t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \left(\mathrm{2}\:+\left({m}−\mathrm{1}\right){t}\:\right)\left(\mathrm{2}+\left({p}−\mathrm{1}\right){t}\right)}\right\} \\ $$$$=\:\mathrm{2}\:\frac{{p}−{m}}{\left(\mathrm{2}\:+\left({m}−\mathrm{1}\right){t}\right)\left(\:\mathrm{2}+\left({p}−\mathrm{1}\right){t}\right)}\:\rightarrow_{{t}\rightarrow\mathrm{0}} \:\:\frac{{p}−{m}}{\mathrm{2}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/May/18

$${excellent}… \\ $$
Answered by ajfour last updated on 27/May/18
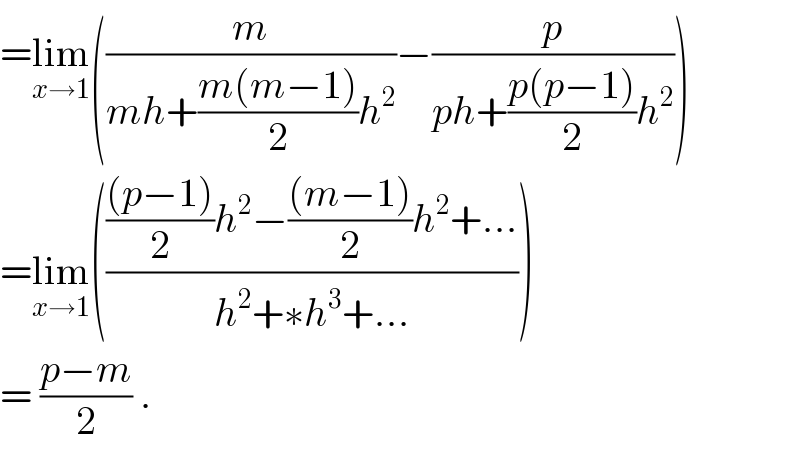
$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{{m}}{{mh}+\frac{{m}\left({m}−\mathrm{1}\right)}{\mathrm{2}}{h}^{\mathrm{2}} }−\frac{{p}}{{ph}+\frac{{p}\left({p}−\mathrm{1}\right)}{\mathrm{2}}{h}^{\mathrm{2}} }\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\frac{\left({p}−\mathrm{1}\right)}{\mathrm{2}}{h}^{\mathrm{2}} −\frac{\left({m}−\mathrm{1}\right)}{\mathrm{2}}{h}^{\mathrm{2}} +…}{{h}^{\mathrm{2}} +\ast{h}^{\mathrm{3}} +…}\right) \\ $$$$=\:\frac{{p}−{m}}{\mathrm{2}}\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/May/18
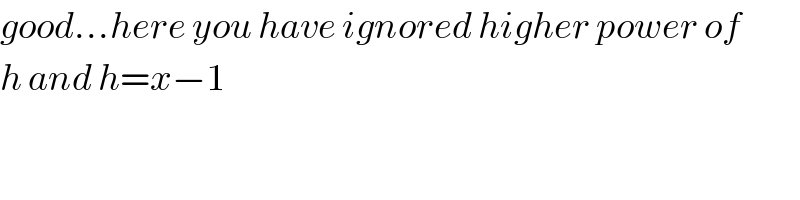
$${good}…{here}\:{you}\:{have}\:{ignored}\:{higher}\:{power}\:{of} \\ $$$${h}\:{and}\:{h}={x}−\mathrm{1} \\ $$
