Menu Close

Question-36034

Tinku Tara 0 Comments
Pin




Question Number 36034 by solihin last updated on 27/May/18
Commented by abdo mathsup 649 cc last updated on 27/May/18
we have z^− (z−i) =10 +2i let put z =x+iy ⇒ (x−iy)(x+iy−i) =10 +2i ⇔ x^2 +ixy −ix −ixy +y^2 −y =10 +2i ⇔ x^2 +y^2 −y + −ix =10 +2i ⇔ x=−2 and x^2 +y^2 −y =10 ⇒ y^2 −y =6 and x=−2 let solve y^2 −y −6 =0 Δ= 1 +24 =25 ⇒ y_1 = ((1 +5)/2) = 3 y_2 = ((1−5)/2) =−2 so z =−2 +3i or z =−2−2i are the solutions for this equation .
$${we}\:{have}\:\overset{−} {{z}}\left({z}−{i}\right)\:=\mathrm{10}\:+\mathrm{2}{i}\:\:{let}\:{put}\:\:{z}\:={x}+{iy}\:\Rightarrow \\ $$$$\left({x}−{iy}\right)\left({x}+{iy}−{i}\right)\:=\mathrm{10}\:+\mathrm{2}{i}\:\Leftrightarrow \\ $$$${x}^{\mathrm{2}} \:+{ixy}\:−{ix}\:−{ixy}\:+{y}^{\mathrm{2}} \:−{y}\:=\mathrm{10}\:+\mathrm{2}{i}\:\Leftrightarrow \\ $$$${x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:−{y}\:\:+\:−{ix}\:\:=\mathrm{10}\:+\mathrm{2}{i}\:\Leftrightarrow \\ $$$${x}=−\mathrm{2}\:{and}\:\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:−{y}\:=\mathrm{10}\:\Rightarrow \\ $$$${y}^{\mathrm{2}} −{y}\:=\mathrm{6}\:{and}\:\:{x}=−\mathrm{2}\:\:{let}\:{solve}\:{y}^{\mathrm{2}} \:−{y}\:−\mathrm{6}\:=\mathrm{0} \\ $$$$\Delta=\:\mathrm{1}\:+\mathrm{24}\:=\mathrm{25}\:\Rightarrow\:{y}_{\mathrm{1}} =\:\frac{\mathrm{1}\:+\mathrm{5}}{\mathrm{2}}\:=\:\mathrm{3} \\ $$$${y}_{\mathrm{2}} \:=\:\frac{\mathrm{1}−\mathrm{5}}{\mathrm{2}}\:=−\mathrm{2}\:\:\:{so}\:{z}\:=−\mathrm{2}\:+\mathrm{3}{i}\:{or}\:{z}\:=−\mathrm{2}−\mathrm{2}{i}\:{are} \\ $$$${the}\:{solutions}\:{for}\:{this}\:{equation}\:. \\ $$
Answered by Rasheed.Sindhi last updated on 27/May/18
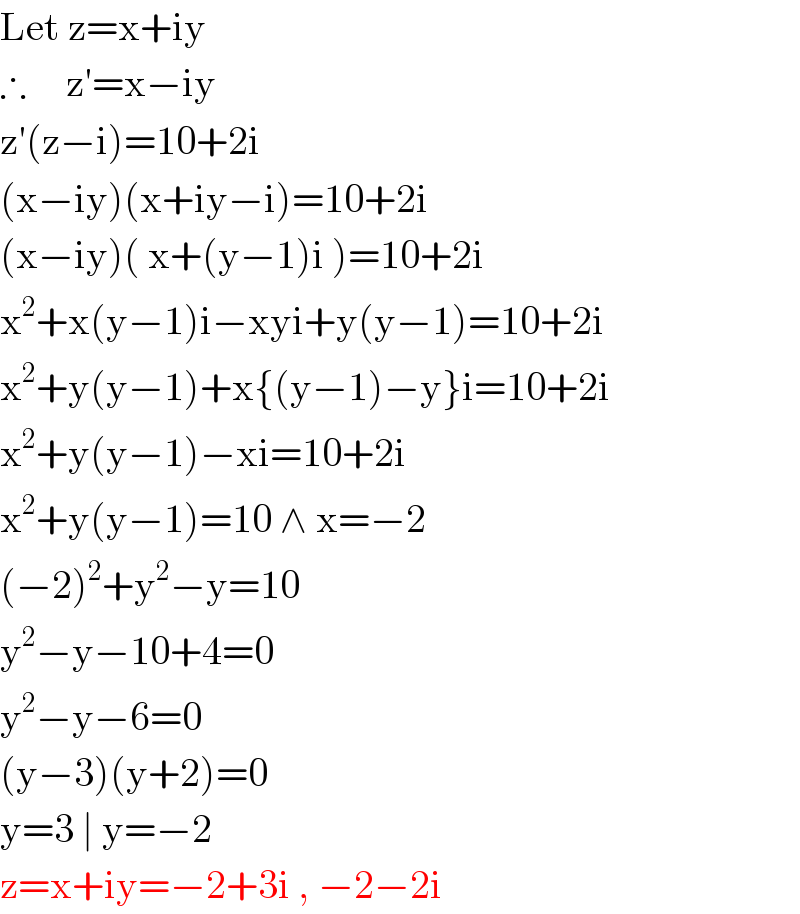
Let z=x+iy ∴ z′=x−iy z′(z−i)=10+2i (x−iy)(x+iy−i)=10+2i (x−iy)( x+(y−1)i )=10+2i x^2 +x(y−1)i−xyi+y(y−1)=10+2i x^2 +y(y−1)+x{(y−1)−y}i=10+2i x^2 +y(y−1)−xi=10+2i x^2 +y(y−1)=10 ∧ x=−2 (−2)^2 +y^2 −y=10 y^2 −y−10+4=0 y^2 −y−6=0 (y−3)(y+2)=0 y=3 ∣ y=−2 z=x+iy=−2+3i , −2−2i
$$\mathrm{Let}\:\mathrm{z}=\mathrm{x}+\mathrm{iy} \\ $$$$\therefore\:\:\:\:\:\mathrm{z}'=\mathrm{x}−\mathrm{iy} \\ $$$$\mathrm{z}'\left(\mathrm{z}−\mathrm{i}\right)=\mathrm{10}+\mathrm{2i} \\ $$$$\left(\mathrm{x}−\mathrm{iy}\right)\left(\mathrm{x}+\mathrm{iy}−\mathrm{i}\right)=\mathrm{10}+\mathrm{2i} \\ $$$$\left(\mathrm{x}−\mathrm{iy}\right)\left(\:\mathrm{x}+\left(\mathrm{y}−\mathrm{1}\right)\mathrm{i}\:\right)=\mathrm{10}+\mathrm{2i} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}\left(\mathrm{y}−\mathrm{1}\right)\mathrm{i}−\mathrm{xyi}+\mathrm{y}\left(\mathrm{y}−\mathrm{1}\right)=\mathrm{10}+\mathrm{2i} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}\left(\mathrm{y}−\mathrm{1}\right)+\mathrm{x}\left\{\left(\mathrm{y}−\mathrm{1}\right)−\mathrm{y}\right\}\mathrm{i}=\mathrm{10}+\mathrm{2i} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}\left(\mathrm{y}−\mathrm{1}\right)−\mathrm{xi}=\mathrm{10}+\mathrm{2i} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}\left(\mathrm{y}−\mathrm{1}\right)=\mathrm{10}\:\wedge\:\mathrm{x}=−\mathrm{2} \\ $$$$\left(−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{y}=\mathrm{10} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{y}−\mathrm{10}+\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{y}−\mathrm{6}=\mathrm{0} \\ $$$$\left(\mathrm{y}−\mathrm{3}\right)\left(\mathrm{y}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{y}=\mathrm{3}\:\mid\:\mathrm{y}=−\mathrm{2} \\ $$$$\mathrm{z}=\mathrm{x}+\mathrm{iy}=−\mathrm{2}+\mathrm{3i}\:,\:−\mathrm{2}−\mathrm{2i} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *