Question-36061

Question Number 36061 by Raj Singh last updated on 28/May/18

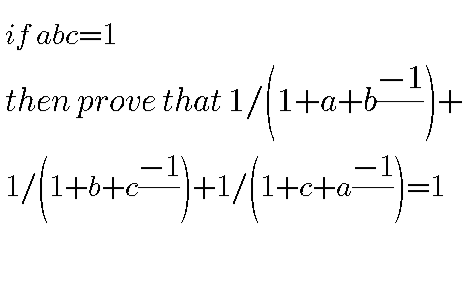
Commented by Rasheed.Sindhi last updated on 28/May/18

Not related to the above question. Dear Abu behi, I ′ve discovered relation between your questions #35844 & #35892. And now I know that you′ve a solution of Q#35892 (and therefore also of Q# 35844).But wait... Let Mr tanmay & S@ty@m complete their trials. BTW Do you like to be called Abu behi by me? If not I will ever call you Mr Behi.

$$\mathcal{N}{ot}\:{related}\:{to}\:{the}\:{above}\:{question}. \\ $$$$\mathcal{D}\mathrm{ear}\:\mathrm{Abu}\:\mathrm{behi}, \\ $$$$\mathcal{I}\:'\mathrm{ve}\:\mathrm{discovered}\:\mathrm{relation}\:\mathrm{between}\:\mathrm{your} \\ $$$$\mathrm{questions}\:#\mathrm{35844}\:\&\:#\mathrm{35892}. \\ $$$$\mathrm{And}\:\mathrm{now}\:\mathrm{I}\:\mathrm{know}\:\mathrm{that}\:\mathrm{you}'\mathrm{ve}\:\mathrm{a}\:\mathrm{solution} \\ $$$$\mathrm{of}\:\mathrm{Q}#\mathrm{35892}\:\left(\mathrm{and}\:\mathrm{therefore}\:\mathrm{also}\:\mathrm{of}\:\mathrm{Q}#\right. \\ $$$$\left.\mathrm{35844}\right).\mathrm{But}\:\mathrm{wait}… \\ $$$$\mathrm{Let}\:\mathrm{Mr}\:\mathrm{tanmay}\:\&\:\mathrm{S}@\mathrm{ty}@\mathrm{m}\:\mathrm{complete} \\ $$$$\mathrm{their}\:\mathrm{trials}. \\ $$$$\mathcal{BTW} \\ $$$$\mathcal{D}\mathrm{o}\:\mathrm{you}\:\mathrm{like}\:\mathrm{to}\:\mathrm{be}\:\mathrm{called}\:\mathrm{Abu}\:\mathrm{behi}\:\mathrm{by}\:\mathrm{me}? \\ $$$$\mathrm{If}\:\mathrm{not}\:\mathrm{I}\:\mathrm{will}\:\mathrm{ever}\:\mathrm{call}\:\mathrm{you}\:\mathrm{Mr}\:\mathrm{Behi}. \\ $$

Commented by behi83417@gmail.com last updated on 28/May/18

$${dear}\:{mr}\:{Rasheed}!{you}\:{are}\:{right}\:{and} \\ $$$${you}\:{are}\:{welcome}. \\ $$

Answered by math1967 last updated on 28/May/18

I think L.H.S(1/(1+a+b^(−1) ))+(1/(1+b+c^(−1) ))+(1/(1+c+a^(−1) )) =(1/(1+a+(1/b)))+(1/(1+b+(1/c)))+(1/(1+c+(1/a))) =(b/(b+ab+1))+(1/(1+b+ab))+(1/(1+(1/(ab))+(1/a))) [∵abc=1,∴(1/c)=ab and c=(1/(ab))] =(b/(b+ab+1))+(1/(b+ab+1))+((ab)/(ab+1+b)) =((b+1+ab)/(b+1+ab))=1=R.H.S Am I correct?

$${I}\:{think}\: \\ $$$${L}.{H}.{S}\frac{\mathrm{1}}{\mathrm{1}+{a}+{b}^{−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{1}+{b}+{c}^{−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{1}+{c}+{a}^{−\mathrm{1}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+{a}+\frac{\mathrm{1}}{{b}}}+\frac{\mathrm{1}}{\mathrm{1}+{b}+\frac{\mathrm{1}}{{c}}}+\frac{\mathrm{1}}{\mathrm{1}+{c}+\frac{\mathrm{1}}{{a}}} \\ $$$$=\frac{{b}}{{b}+{ab}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+{b}+{ab}}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{a}}} \\ $$$$\left[\because{abc}=\mathrm{1},\therefore\frac{\mathrm{1}}{{c}}={ab}\:{and}\:{c}=\frac{\mathrm{1}}{{ab}}\right] \\ $$$$=\frac{{b}}{{b}+{ab}+\mathrm{1}}+\frac{\mathrm{1}}{{b}+{ab}+\mathrm{1}}+\frac{{ab}}{{ab}+\mathrm{1}+{b}} \\ $$$$=\frac{{b}+\mathrm{1}+{ab}}{{b}+\mathrm{1}+{ab}}=\mathrm{1}={R}.{H}.{S} \\ $$$${Am}\:{I}\:{correct}? \\ $$

Commented by Rasheed.Sindhi last updated on 28/May/18

$$\mathrm{e}^{\mathrm{x}} \mathrm{cellent}! \\ $$

Commented by math1967 last updated on 29/May/18

$${My}\:{pleasure} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply