Menu Close

Question-36099

Tinku Tara 0 Comments
Pin




Question Number 36099 by rahul 19 last updated on 28/May/18
Commented by rahul 19 last updated on 01/Jun/18
Help in Q. 1.
$$\mathrm{Help}\:\mathrm{in}\:\mathrm{Q}.\:\mathrm{1}. \\ $$
Commented by rahul 19 last updated on 31/Aug/18
Thank you prof Abdo :)
$$\left.\mathrm{Thank}\:\mathrm{you}\:\mathrm{prof}\:\mathrm{Abdo}\::\right) \\ $$
Commented by maxmathsup by imad last updated on 31/Aug/18
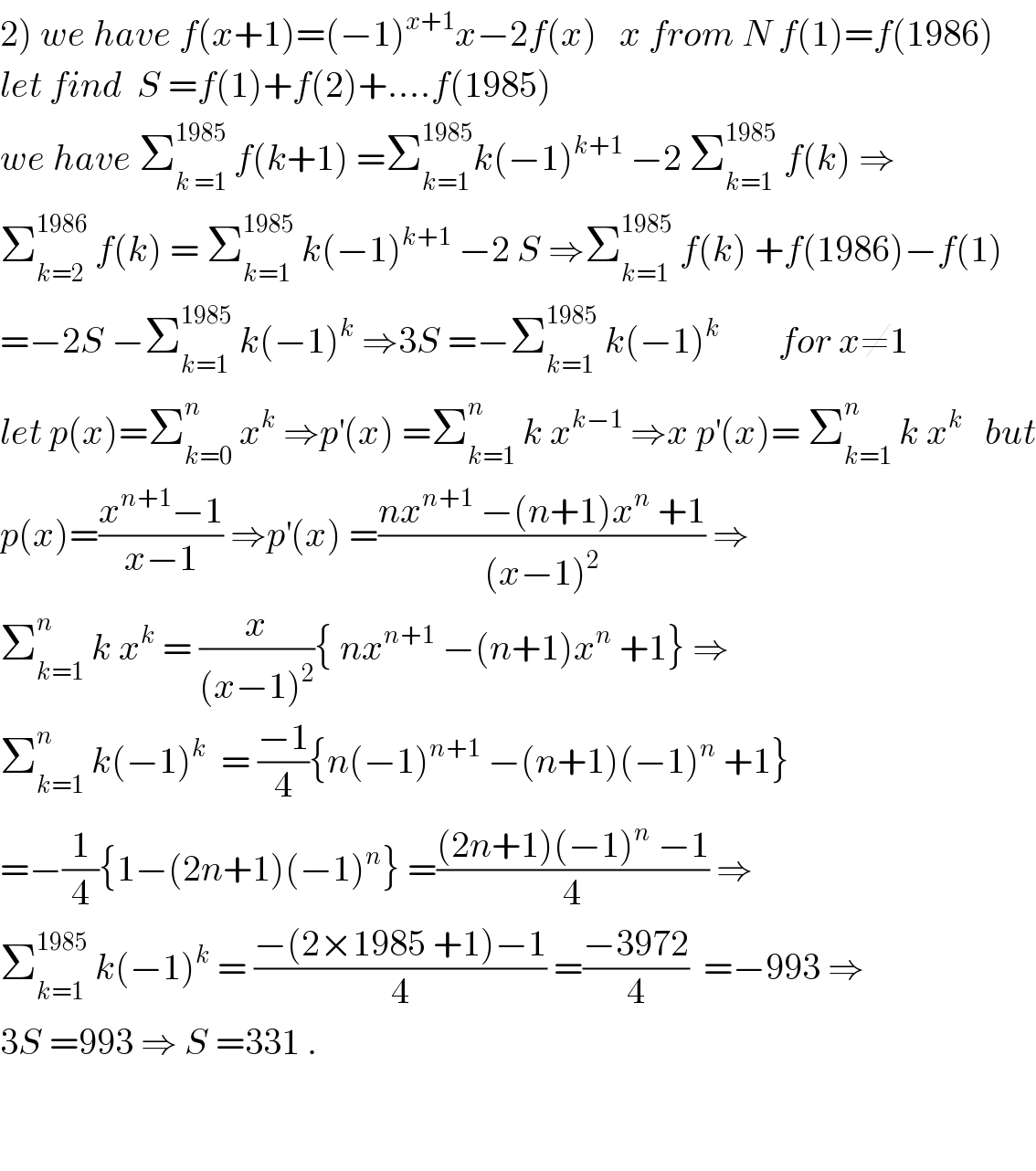
2) we have f(x+1)=(−1)^(x+1) x−2f(x) x from N f(1)=f(1986) let find S =f(1)+f(2)+....f(1985) we have Σ_(k =1) ^(1985) f(k+1) =Σ_(k=1) ^(1985) k(−1)^(k+1) −2 Σ_(k=1) ^(1985) f(k) ⇒ Σ_(k=2) ^(1986) f(k) = Σ_(k=1) ^(1985) k(−1)^(k+1) −2 S ⇒Σ_(k=1) ^(1985) f(k) +f(1986)−f(1) =−2S −Σ_(k=1) ^(1985) k(−1)^k ⇒3S =−Σ_(k=1) ^(1985) k(−1)^k for x≠1 let p(x)=Σ_(k=0) ^n x^k ⇒p^′ (x) =Σ_(k=1) ^n k x^(k−1) ⇒x p^′ (x)= Σ_(k=1) ^n k x^(k ) but p(x)=((x^(n+1) −1)/(x−1)) ⇒p^′ (x) =((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒ Σ_(k=1) ^n k x^k = (x/((x−1)^2 )){ nx^(n+1) −(n+1)x^n +1} ⇒ Σ_(k=1) ^n k(−1)^k = ((−1)/4){n(−1)^(n+1) −(n+1)(−1)^n +1} =−(1/4){1−(2n+1)(−1)^n } =(((2n+1)(−1)^n −1)/4) ⇒ Σ_(k=1) ^(1985) k(−1)^k = ((−(2×1985 +1)−1)/4) =((−3972)/4) =−993 ⇒ 3S =993 ⇒ S =331 .
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}\left({x}+\mathrm{1}\right)=\left(−\mathrm{1}\right)^{{x}+\mathrm{1}} {x}−\mathrm{2}{f}\left({x}\right)\:\:\:{x}\:{from}\:{N}\:{f}\left(\mathrm{1}\right)={f}\left(\mathrm{1986}\right) \\ $$$${let}\:{find}\:\:{S}\:={f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)+….{f}\left(\mathrm{1985}\right) \\ $$$${we}\:{have}\:\sum_{{k}\:=\mathrm{1}} ^{\mathrm{1985}} \:{f}\left({k}+\mathrm{1}\right)\:=\sum_{{k}=\mathrm{1}} ^{\mathrm{1985}} {k}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \:−\mathrm{2}\:\sum_{{k}=\mathrm{1}} ^{\mathrm{1985}} \:{f}\left({k}\right)\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{2}} ^{\mathrm{1986}} \:{f}\left({k}\right)\:=\:\sum_{{k}=\mathrm{1}} ^{\mathrm{1985}} \:{k}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \:−\mathrm{2}\:{S}\:\Rightarrow\sum_{{k}=\mathrm{1}} ^{\mathrm{1985}} \:{f}\left({k}\right)\:+{f}\left(\mathrm{1986}\right)−{f}\left(\mathrm{1}\right) \\ $$$$=−\mathrm{2}{S}\:−\sum_{{k}=\mathrm{1}} ^{\mathrm{1985}} \:{k}\left(−\mathrm{1}\right)^{{k}} \:\Rightarrow\mathrm{3}{S}\:=−\sum_{{k}=\mathrm{1}} ^{\mathrm{1985}} \:{k}\left(−\mathrm{1}\right)^{{k}} \:\:\:\:\:\:\:\:{for}\:{x}\neq\mathrm{1} \\ $$$${let}\:{p}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{x}^{{k}} \:\Rightarrow{p}^{'} \left({x}\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}−\mathrm{1}} \:\Rightarrow{x}\:{p}^{'} \left({x}\right)=\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}\:\:} \:\:{but} \\ $$$${p}\left({x}\right)=\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\:\Rightarrow{p}^{'} \left({x}\right)\:=\frac{{nx}^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right){x}^{{n}} \:+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{x}^{{k}} \:=\:\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\left\{\:{nx}^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right){x}^{{n}} \:+\mathrm{1}\right\}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\left(−\mathrm{1}\right)^{{k}} \:\:=\:\frac{−\mathrm{1}}{\mathrm{4}}\left\{{n}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} \:+\mathrm{1}\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{1}−\left(\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} \right\}\:=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} \:−\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{\mathrm{1985}} \:{k}\left(−\mathrm{1}\right)^{{k}} \:=\:\frac{−\left(\mathrm{2}×\mathrm{1985}\:+\mathrm{1}\right)−\mathrm{1}}{\mathrm{4}}\:=\frac{−\mathrm{3972}}{\mathrm{4}}\:\:=−\mathrm{993}\:\Rightarrow \\ $$$$\mathrm{3}{S}\:=\mathrm{993}\:\Rightarrow\:{S}\:=\mathrm{331}\:. \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 31/Aug/18
nevermind sir.
$${nevermind}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *