Question Number 36101 by rahul 19 last updated on 28/May/18
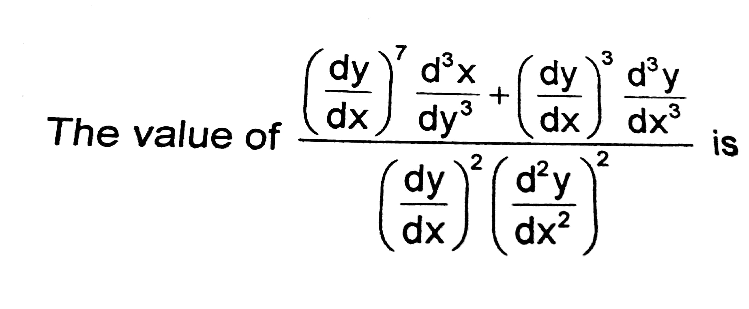
Commented by rahul 19 last updated on 29/May/18
Ans. given is 3.
Commented by tanmay.chaudhury50@gmail.com last updated on 29/May/18

$${pls}\:{check} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 29/May/18
)) now putting the value =((−(7x^6 )^3 ×210x^4 +42x^5 ×3×49x^(12) ×42x^5 )/((7x^6 )^6 ))×(1/(7x^6 )) =((42×42×49×3×x^(22) −210×7^3 ×x^(22) )/(7^7 ×x^(42) )) =((7^4 ×3^3 ×2^2 x^(22) −7^4 ×5×3×2x^(22) )/(7^7 ×x^(42) )) =((7^4 ×x^(22) (108−30))/(7^7 ×x^(42) )) =((78)/(343x^(20) ))](https://www.tinkutara.com/question/Q36117.png)
$${y}={f}\left({x}\right)={x}^{\mathrm{7}} \\ $$$$\frac{{dy}}{{dx}}={f}_{\mathrm{1}} \left({x}\right)=\mathrm{7}{x}^{\mathrm{6}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={f}_{\mathrm{2}} \left({x}\right)=\mathrm{42}{x}^{\mathrm{5}} \\ $$$$\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }={f}_{\mathrm{3}} \left({x}\right)=\mathrm{210}{x}^{\mathrm{4}} \\ $$$$\frac{{dx}}{{dy}}=\frac{\mathrm{1}}{{f}_{\mathrm{1}} \left({x}\right)}=\frac{\mathrm{1}}{\mathrm{7}{x}^{\mathrm{6}} } \\ $$$$\frac{{d}^{\mathrm{2}} {x}}{{dy}^{\mathrm{2}} }=\frac{{d}}{{dy}}\left(\frac{{dx}}{{dy}}\right) \\ $$$$\:\:=\frac{{d}}{{dx}}\left\{\frac{\mathrm{1}}{{f}_{\mathrm{1}} \left({x}\right)}\right\}\frac{{dx}}{{dy}} \\ $$$$=\frac{−\mathrm{1}}{\left\{{f}_{\mathrm{1}} \left({x}\right)\right\}^{\mathrm{2}} }×{f}_{\mathrm{2}} \left({x}\right)×\frac{\mathrm{1}}{{f}_{\mathrm{1}} \left({x}\right)}=\frac{−{f}_{\mathrm{2}} \left({x}\right)}{\left\{{f}_{\mathrm{1}} \left({x}\right)\right\}^{\mathrm{3}} }=\frac{−\mathrm{42}{x}^{\mathrm{5}} }{\mathrm{343}{x}^{\mathrm{18}} }=\frac{−\mathrm{6}}{\mathrm{49}{x}^{\mathrm{13}} } \\ $$$$ \\ $$$$\frac{{d}^{\mathrm{3}} {x}}{{dy}^{\mathrm{3}} }=\frac{{d}}{{dy}}\left(\frac{{d}^{\mathrm{2}} {x}}{{dy}^{\mathrm{2}} }\right)=\frac{{d}}{{dx}}\left\{\frac{−{f}_{\mathrm{2}} \left({x}\right)}{\left({f}_{\mathrm{1}} \left({x}\right)\right)^{\mathrm{3}} }\right\}×\frac{{dx}}{{dy}} \\ $$$$=\left[\frac{−\left\{{f}_{\mathrm{1}} \left({x}\right)\right\}^{\mathrm{3}} ×{f}_{\mathrm{3}} \left({x}\right)+{f}_{\mathrm{2}} \left({x}\right)×\mathrm{3}\left\{{f}_{\mathrm{1}} \left({x}\right)\right\}^{\mathrm{2}} ×{f}_{\mathrm{2}} \left({x}\right)}{\left\{{f}_{\mathrm{1}} \left({x}\right)\right\}^{\mathrm{6}} }\right]\frac{\mathrm{1}}{{f}_{\mathrm{1}} \left({x}\right)} \\ $$$${now}\:{putting}\:{the}\:{value} \\ $$$$=\frac{−\left(\mathrm{7}{x}^{\mathrm{6}} \right)^{\mathrm{3}} ×\mathrm{210}{x}^{\mathrm{4}} +\mathrm{42}{x}^{\mathrm{5}} ×\mathrm{3}×\mathrm{49}{x}^{\mathrm{12}} ×\mathrm{42}{x}^{\mathrm{5}} }{\left(\mathrm{7}{x}^{\mathrm{6}} \right)^{\mathrm{6}} }×\frac{\mathrm{1}}{\mathrm{7}{x}^{\mathrm{6}} } \\ $$$$=\frac{\mathrm{42}×\mathrm{42}×\mathrm{49}×\mathrm{3}×{x}^{\mathrm{22}} −\mathrm{210}×\mathrm{7}^{\mathrm{3}} ×{x}^{\mathrm{22}} }{\mathrm{7}^{\mathrm{7}} ×{x}^{\mathrm{42}} } \\ $$$$=\frac{\mathrm{7}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{3}} ×\mathrm{2}^{\mathrm{2}} {x}^{\mathrm{22}} −\mathrm{7}^{\mathrm{4}} ×\mathrm{5}×\mathrm{3}×\mathrm{2}{x}^{\mathrm{22}} }{\mathrm{7}^{\mathrm{7}} ×{x}^{\mathrm{42}} } \\ $$$$=\frac{\mathrm{7}^{\mathrm{4}} ×{x}^{\mathrm{22}} \left(\mathrm{108}−\mathrm{30}\right)}{\mathrm{7}^{\mathrm{7}} ×{x}^{\mathrm{42}} } \\ $$$$=\frac{\mathrm{78}}{\mathrm{343}{x}^{\mathrm{20}} } \\ $$
Commented by rahul 19 last updated on 30/May/18
sir, why 3 is not coming as the final answer .
This expression is true for all x,y.
Isn't it ?
Commented by rahul 19 last updated on 31/May/18
??����
Answered by ajfour last updated on 29/May/18
![(d^3 x/dy^3 )=(d/dy)[(d/dy)((dy/dx))^(−1) ]=(d/dy)[−((dy/dx))^(−2) (d^2 y/dx^2 )((dx/dy))] (d^3 x/dy^2 )=(d/dx)[−((dy/dx))^(−3) (d^2 y/dx^2 )]((dx/dy)) =3((d^2 y/dx^2 ))((dy/dx))^(−5) −((dy/dx))^(−4) (d^3 y/dx^3 ) ⇒ ((dy/dx))^7 (d^3 x/dy^3 )+((dy/dx))^3 (d^2 y/dx^2 ) =3((dy/dx))^2 (d^2 y/dx^2 ) or ((((dy/dx))^7 ((d^3 x/dy^3 ))+((dy/dx))^3 (d^2 y/dx^2 ))/(((dy/dx))^2 (d^2 y/dx^2 ))) = 3 .](https://www.tinkutara.com/question/Q36134.png)
$$\frac{{d}^{\mathrm{3}} {x}}{{dy}^{\mathrm{3}} }=\frac{{d}}{{dy}}\left[\frac{{d}}{{dy}}\left(\frac{{dy}}{{dx}}\right)^{−\mathrm{1}} \right]=\frac{{d}}{{dy}}\left[−\left(\frac{{dy}}{{dx}}\right)^{−\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\left(\frac{{dx}}{{dy}}\right)\right] \\ $$$$\frac{{d}^{\mathrm{3}} {x}}{{dy}^{\mathrm{2}} }=\frac{{d}}{{dx}}\left[−\left(\frac{{dy}}{{dx}}\right)^{−\mathrm{3}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right]\left(\frac{{dx}}{{dy}}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{3}\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)\left(\frac{{dy}}{{dx}}\right)^{−\mathrm{5}} −\left(\frac{{dy}}{{dx}}\right)^{−\mathrm{4}} \frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} } \\ $$$$\Rightarrow\:\left(\frac{{dy}}{{dx}}\right)^{\mathrm{7}} \frac{{d}^{\mathrm{3}} {x}}{{dy}^{\mathrm{3}} }+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{3}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\mathrm{3}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$$${or}\:\:\:\:\:\frac{\left(\frac{{dy}}{{dx}}\right)^{\mathrm{7}} \left(\frac{{d}^{\mathrm{3}} {x}}{{dy}^{\mathrm{3}} }\right)+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{3}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }}{\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }}\:=\:\mathrm{3}\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 29/May/18

$${excellent}… \\ $$
Commented by ajfour last updated on 29/May/18

$${mistake}\:{in}\:{question},\:{in}\:{the} \\ $$$${denominator}\:{we}\:{should}\:{have} \\ $$$$\:\:\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:. \\ $$
Commented by rahul 19 last updated on 30/May/18
Thank you sir .
