Question Number 36366 by chakraborty ankit last updated on 01/Jun/18

Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jun/18
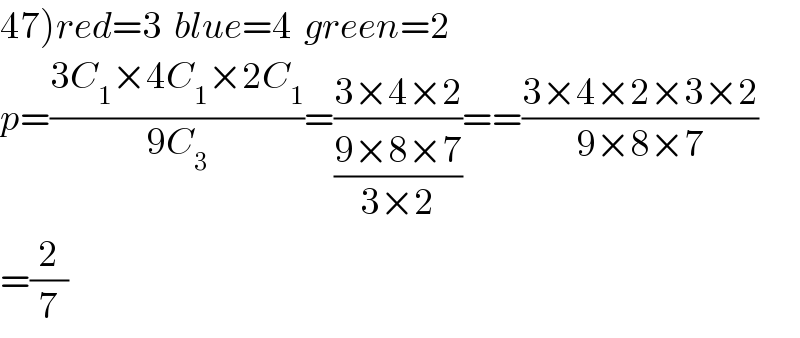
$$\left.\mathrm{47}\right){red}=\mathrm{3}\:\:{blue}=\mathrm{4}\:\:{green}=\mathrm{2} \\ $$$${p}=\frac{\mathrm{3}{C}_{\mathrm{1}} ×\mathrm{4}{C}_{\mathrm{1}} ×\mathrm{2}{C}_{\mathrm{1}} }{\mathrm{9}{C}_{\mathrm{3}} }=\frac{\mathrm{3}×\mathrm{4}×\mathrm{2}}{\frac{\mathrm{9}×\mathrm{8}×\mathrm{7}}{\mathrm{3}×\mathrm{2}}}==\frac{\mathrm{3}×\mathrm{4}×\mathrm{2}×\mathrm{3}×\mathrm{2}}{\mathrm{9}×\mathrm{8}×\mathrm{7}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{7}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jun/18
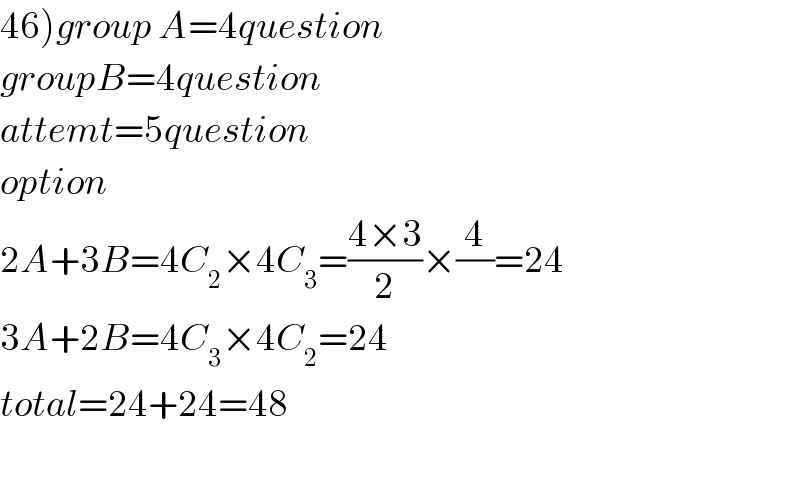
$$\left.\mathrm{46}\right){group}\:{A}=\mathrm{4}{question} \\ $$$${groupB}=\mathrm{4}{question} \\ $$$${attemt}=\mathrm{5}{question} \\ $$$${option} \\ $$$$\mathrm{2}{A}+\mathrm{3}{B}=\mathrm{4}{C}_{\mathrm{2}} ×\mathrm{4}{C}_{\mathrm{3}} =\frac{\mathrm{4}×\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{4}}{}=\mathrm{24} \\ $$$$\mathrm{3}{A}+\mathrm{2}{B}=\mathrm{4}{C}_{\mathrm{3}} ×\mathrm{4}{C}_{\mathrm{2}} =\mathrm{24} \\ $$$${total}=\mathrm{24}+\mathrm{24}=\mathrm{48} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jun/18
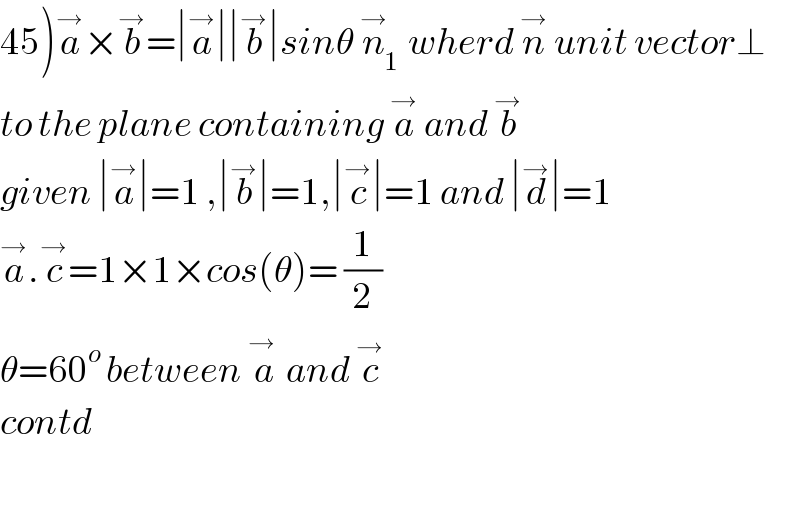
$$\left.\mathrm{45}\right)\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}=\mid\overset{\rightarrow} {{a}}\mid\mid\overset{\rightarrow} {{b}}\mid{sin}\theta\:\overset{\rightarrow} {{n}}_{\mathrm{1}} \:{wherd}\:\overset{\rightarrow} {{n}}\:{unit}\:{vector}\bot \\ $$$${to}\:{the}\:{plane}\:{containing}\:\overset{\rightarrow} {{a}}\:{and}\:\overset{\rightarrow} {{b}} \\ $$$${given}\:\mid\overset{\rightarrow} {{a}}\mid=\mathrm{1}\:,\mid\overset{\rightarrow} {{b}}\mid=\mathrm{1},\mid\overset{\rightarrow} {{c}}\mid=\mathrm{1}\:{and}\:\mid\overset{\rightarrow} {{d}}\mid=\mathrm{1} \\ $$$$\overset{\rightarrow} {{a}}.\overset{\rightarrow} {{c}}=\mathrm{1}×\mathrm{1}×{cos}\left(\theta\right)=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\theta=\mathrm{60}^{{o}\:} {between}\:\overset{\rightarrow\:} {{a}}\:{and}\:\overset{\rightarrow} {{c}} \\ $$$${contd} \\ $$$$ \\ $$
Commented by chakraborty ankit last updated on 02/Jun/18

$${Thank}\:{you}\:{sir} \\ $$
