Menu Close

Question-36563

Tinku Tara 0 Comments
Pin




Question Number 36563 by bshahid010@gmail.com last updated on 03/Jun/18
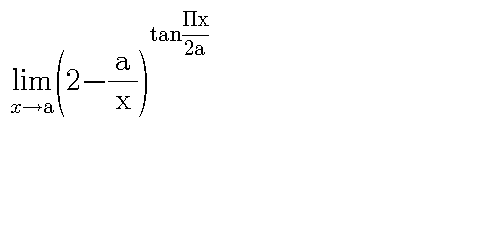
Commented by prof Abdo imad last updated on 03/Jun/18
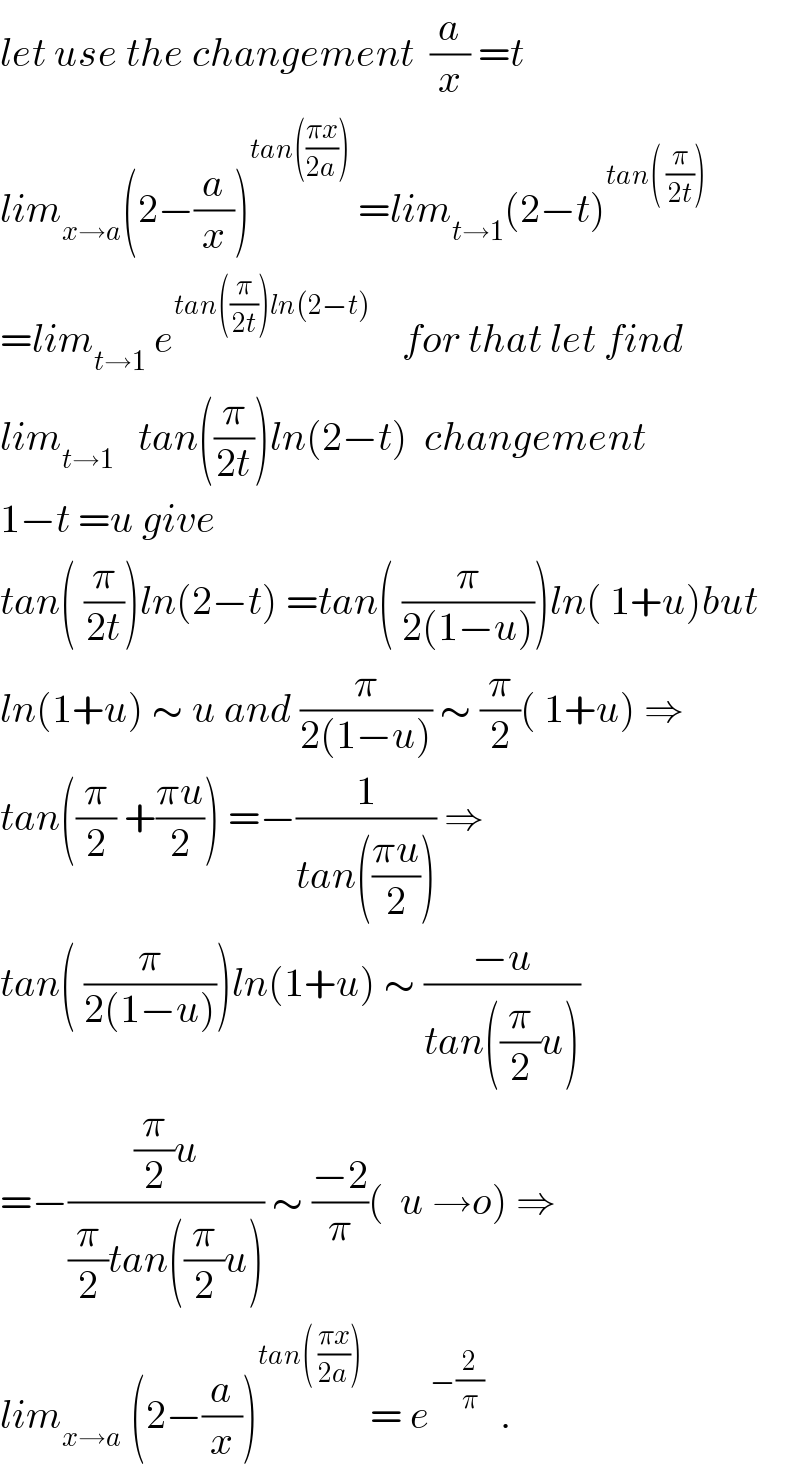
let use the changement (a/x) =t lim_(x→a) (2−(a/x))^(tan(((πx)/(2a)))) =lim_(t→1) (2−t)^(tan( (π/(2t)))) =lim_(t→1) e^(tan((π/(2t)))ln(2−t)) for that let find lim_(t→1) tan((π/(2t)))ln(2−t) changement 1−t =u give tan( (π/(2t)))ln(2−t) =tan( (π/(2(1−u))))ln( 1+u)but ln(1+u) ∼ u and (π/(2(1−u))) ∼ (π/2)( 1+u) ⇒ tan((π/2) +((πu)/2)) =−(1/(tan(((πu)/2)))) ⇒ tan( (π/(2(1−u))))ln(1+u) ∼ ((−u)/(tan((π/2)u))) =−(((π/2)u)/((π/2)tan((π/2)u))) ∼ ((−2)/π)( u →o) ⇒ lim_(x→a) (2−(a/x))^(tan( ((πx)/(2a)))) = e^(−(2/π)) .
$${let}\:{use}\:{the}\:{changement}\:\:\frac{{a}}{{x}}\:={t} \\ $$$${lim}_{{x}\rightarrow{a}} \left(\mathrm{2}−\frac{{a}}{{x}}\right)^{{tan}\left(\frac{\pi{x}}{\mathrm{2}{a}}\right)} \:={lim}_{{t}\rightarrow\mathrm{1}} \left(\mathrm{2}−{t}\right)^{{tan}\left(\:\frac{\pi}{\mathrm{2}{t}}\right)} \\ $$$$={lim}_{{t}\rightarrow\mathrm{1}} \:{e}^{{tan}\left(\frac{\pi}{\mathrm{2}{t}}\right){ln}\left(\mathrm{2}−{t}\right)} \:\:\:\:{for}\:{that}\:{let}\:{find} \\ $$$${lim}_{{t}\rightarrow\mathrm{1}} \:\:\:{tan}\left(\frac{\pi}{\mathrm{2}{t}}\right){ln}\left(\mathrm{2}−{t}\right)\:\:{changement} \\ $$$$\mathrm{1}−{t}\:={u}\:{give} \\ $$$${tan}\left(\:\frac{\pi}{\mathrm{2}{t}}\right){ln}\left(\mathrm{2}−{t}\right)\:={tan}\left(\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}−{u}\right)}\right){ln}\left(\:\mathrm{1}+{u}\right){but} \\ $$$${ln}\left(\mathrm{1}+{u}\right)\:\sim\:{u}\:{and}\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}−{u}\right)}\:\sim\:\frac{\pi}{\mathrm{2}}\left(\:\mathrm{1}+{u}\right)\:\Rightarrow \\ $$$${tan}\left(\frac{\pi}{\mathrm{2}}\:+\frac{\pi{u}}{\mathrm{2}}\right)\:=−\frac{\mathrm{1}}{{tan}\left(\frac{\pi{u}}{\mathrm{2}}\right)}\:\Rightarrow \\ $$$${tan}\left(\:\frac{\pi}{\mathrm{2}\left(\mathrm{1}−{u}\right)}\right){ln}\left(\mathrm{1}+{u}\right)\:\sim\:\frac{−{u}}{{tan}\left(\frac{\pi}{\mathrm{2}}{u}\right)} \\ $$$$=−\frac{\frac{\pi}{\mathrm{2}}{u}}{\frac{\pi}{\mathrm{2}}{tan}\left(\frac{\pi}{\mathrm{2}}{u}\right)}\:\sim\:\frac{−\mathrm{2}}{\pi}\left(\:\:{u}\:\rightarrow{o}\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow{a}} \:\left(\mathrm{2}−\frac{{a}}{{x}}\right)^{{tan}\left(\:\frac{\pi{x}}{\mathrm{2}{a}}\right)} \:=\:{e}^{−\frac{\mathrm{2}}{\pi}} \:\:. \\ $$
Answered by ajfour last updated on 03/Jun/18
L=lim_(x→a) {[1+(1−(a/x))]^(1/(1−(a/x))) }^((1−(a/x))/(tan ((π/2)(1−(x/a))))) ⇒ L = e^(2/π) .
$${L}=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\left\{\left[\mathrm{1}+\left(\mathrm{1}−\frac{{a}}{{x}}\right)\right]^{\frac{\mathrm{1}}{\mathrm{1}−\frac{{a}}{{x}}}} \right\}^{\frac{\mathrm{1}−\frac{{a}}{{x}}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\frac{{x}}{{a}}\right)\right)}} \\ $$$$\Rightarrow\:\:{L}\:=\:{e}^{\frac{\mathrm{2}}{\pi}} \:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *