Menu Close

Question-36660

Tinku Tara 0 Comments
Pin




Question Number 36660 by Tinkutara last updated on 03/Jun/18
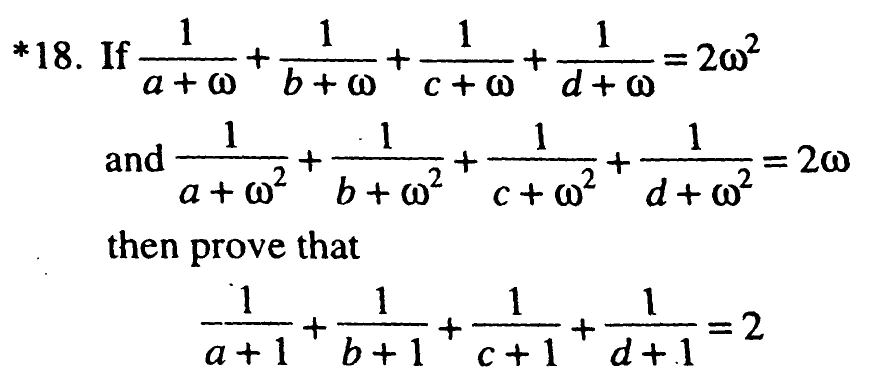
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Jun/18
(1/(a+w))+(1/(b+w))+(1/(c+w))+(1/(d+w))=((2w^3 )/w)=(2/w) (1/(a+w^2 ))+(1/(b+w^2 ))+(1/(c+w^2 ))+(1/(d+w^2 ))=((2w^3 )/w^2 )=(2/w^2 ) nw (1/(a+x))+(1/(b+x))+(1/(c+x))+(1/(d+x))=(2/x) this equation have...eqn1 roots w and w^2 ...because if in place of x put w first identity and if x replaced by w^2 second one... ((b+x+a+x)/(ab+ax+bx+x^2 ))+((d+x+c+x)/(cd+cx+dx+x^2 ))−(2/x)=0 ((a+b+2x)/(ab+ax+bx+x^2 ))−(1/x)+((c+d+2x)/(cd+cx+dx+x^2 ))−(1/x)=0 ((ax+bx+2x^2 −ab−ax−bx−x^2 )/((ab+ax+bx+x^2 )x))+ ((cx+dx+2x^2 −cd−cx−dx−x^2 ))/((cd+cx+dx+x^2 )x))=0 ((x^2 −ab)/(N_1 x))+((x^2 −cd)/(N_2 x))=0 (x^2 −ab)(cd+cx+dx+x^2 )+(x^2 −cd)(ab+ax+bx +x^2 )=0 x^4 +cx^3 +dx^3 +cdx^2 −abcd−abcx−abdx−abx^2 +x^4 +ax^3 +bx^3 +abx^2 −abcd−acdx−bcdx− cdx^2 =0 2x^4 +x^3 (a+b+c+d)+x^2 (0)+x(−abc−abd−acd −bcd)−2abcd=0 four roots w+w^2 +α+β=−(a+b+c+d)/2 w×w^2 +wα+wβ+w^2 α+w^2 β+αβ=0 1+α(w+w^2 )+β(w+w^2 )+αβ=0 1−α−β+αβ=0 (1−α)−β(1−α)=0 (1−α)(1−β)=0 so either α=1 or β=1 so eqn (1/(a+x))+(1/(b+x))+(1/(c+x))+(1/(d+x))=(2/x) has four roots..w,w^2 ,1 foirth root to find since 1 is root hence x can be replaced by 1 hence (1/(a+1))+(1/(b+1))+(1/(c+1))+(1/(1+1))=(2/1) proved i have taken hintsfrom higher algebra Barnard and child and Hall and knkght to prove it
$$\frac{\mathrm{1}}{{a}+{w}}+\frac{\mathrm{1}}{{b}+{w}}+\frac{\mathrm{1}}{{c}+{w}}+\frac{\mathrm{1}}{{d}+{w}}=\frac{\mathrm{2}{w}^{\mathrm{3}} }{{w}}=\frac{\mathrm{2}}{{w}} \\ $$$$\frac{\mathrm{1}}{{a}+{w}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}+{w}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}+{w}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}+{w}^{\mathrm{2}} }=\frac{\mathrm{2}{w}^{\mathrm{3}} }{{w}^{\mathrm{2}} }=\frac{\mathrm{2}}{{w}^{\mathrm{2}} } \\ $$$${nw} \\ $$$$\frac{\mathrm{1}}{{a}+{x}}+\frac{\mathrm{1}}{{b}+{x}}+\frac{\mathrm{1}}{{c}+{x}}+\frac{\mathrm{1}}{{d}+{x}}=\frac{\mathrm{2}}{{x}}\:\:{this}\:{equation}\:{have}…{eqn}\mathrm{1} \\ $$$${roots}\:\:{w}\:{and}\:{w}^{\mathrm{2}} …{because}\:{if}\:{in}\:{place}\:{of}\:{x}\:{put}\:{w} \\ $$$${first}\:{identity}\:\:{and}\:{if}\:{x}\:{replaced}\:{by}\:{w}^{\mathrm{2}} \\ $$$${second}\:{one}… \\ $$$$\frac{{b}+{x}+{a}+{x}}{{ab}+{ax}+{bx}+{x}^{\mathrm{2}} }+\frac{{d}+{x}+{c}+{x}}{{cd}+{cx}+{dx}+{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{{x}}=\mathrm{0} \\ $$$$\frac{{a}+{b}+\mathrm{2}{x}}{{ab}+{ax}+{bx}+{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}+\frac{{c}+{d}+\mathrm{2}{x}}{{cd}+{cx}+{dx}+{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}=\mathrm{0} \\ $$$$\frac{{ax}+{bx}+\mathrm{2}{x}^{\mathrm{2}} \:−{ab}−{ax}−{bx}−{x}^{\mathrm{2}} }{\left({ab}+{ax}+{bx}+{x}^{\mathrm{2}} \right){x}}+ \\ $$$$\frac{\left.{cx}+{dx}+\mathrm{2}{x}^{\mathrm{2}} −{cd}−{cx}−{dx}−{x}^{\mathrm{2}} \right)}{\left({cd}+{cx}+{dx}+{x}^{\mathrm{2}} \right){x}}=\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{2}} −{ab}}{{N}_{\mathrm{1}} {x}}+\frac{{x}^{\mathrm{2}} −{cd}}{{N}_{\mathrm{2}} {x}}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −{ab}\right)\left({cd}+{cx}+{dx}+{x}^{\mathrm{2}} \right)+\left({x}^{\mathrm{2}} −{cd}\right)\left({ab}+{ax}+{bx}\right. \\ $$$$\left.+{x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} +{cx}^{\mathrm{3}} +{dx}^{\mathrm{3}} +{cdx}^{\mathrm{2}} −{abcd}−{abcx}−{abdx}−{abx}^{\mathrm{2}} \\ $$$$+{x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{3}} \:+{abx}^{\mathrm{2}} −{abcd}−{acdx}−{bcdx}− \\ $$$${cdx}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{4}} +{x}^{\mathrm{3}} \left({a}+{b}+{c}+{d}\right)+{x}^{\mathrm{2}} \left(\mathrm{0}\right)+{x}\left(−{abc}−{abd}−{acd}\right. \\ $$$$\left.\:−{bcd}\right)−\mathrm{2}{abcd}=\mathrm{0} \\ $$$${four}\:{roots}\:{w}+{w}^{\mathrm{2}} +\alpha+\beta=−\left({a}+{b}+{c}+{d}\right)/\mathrm{2} \\ $$$${w}×{w}^{\mathrm{2}} +{w}\alpha+{w}\beta+{w}^{\mathrm{2}} \alpha+{w}^{\mathrm{2}} \beta+\alpha\beta=\mathrm{0} \\ $$$$\mathrm{1}+\alpha\left({w}+{w}^{\mathrm{2}} \right)+\beta\left({w}+{w}^{\mathrm{2}} \right)+\alpha\beta=\mathrm{0} \\ $$$$\mathrm{1}−\alpha−\beta+\alpha\beta=\mathrm{0} \\ $$$$\left(\mathrm{1}−\alpha\right)−\beta\left(\mathrm{1}−\alpha\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}−\alpha\right)\left(\mathrm{1}−\beta\right)=\mathrm{0} \\ $$$${so}\:{either}\:\alpha=\mathrm{1}\:{or}\:\beta=\mathrm{1} \\ $$$${so}\:{eqn} \\ $$$$\frac{\mathrm{1}}{{a}+{x}}+\frac{\mathrm{1}}{{b}+{x}}+\frac{\mathrm{1}}{{c}+{x}}+\frac{\mathrm{1}}{{d}+{x}}=\frac{\mathrm{2}}{{x}} \\ $$$${has}\:{four}\:\:{roots}..{w},{w}^{\mathrm{2}} ,\mathrm{1}\:{foirth}\:{root}\:{to}\:{find} \\ $$$${since}\:\mathrm{1}\:{is}\:{root} \\ $$$${hence}\:{x}\:{can}\:{be}\:{replaced}\:{by}\:\mathrm{1} \\ $$$${hence}\: \\ $$$$\frac{\mathrm{1}}{{a}+\mathrm{1}}+\frac{\mathrm{1}}{{b}+\mathrm{1}}+\frac{\mathrm{1}}{{c}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{1}}\:{proved} \\ $$$${i}\:{have}\:{taken}\:{hintsfrom}\:{higher}\:{algebra} \\ $$$${Barnard}\:{and}\:{child}\:{and}\:{Hall}\:{and}\:{knkght}\:{to} \\ $$$${prove}\:{it} \\ $$$$ \\ $$$$ \\ $$
Commented by Tinkutara last updated on 05/Jun/18
Thank you very much Sir! I got the answer. ��������

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *