Question Number 37073 by ajfour last updated on 08/Jun/18
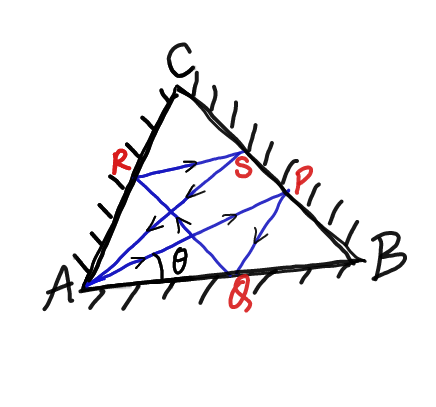
Commented by ajfour last updated on 08/Jun/18

$${If}\:{a}\:{ray}\:{of}\:{light}\:{originate}\:{at}\:{A}, \\ $$$${get}\:{reflected}\:{by}\:{the}\:{sides}\:{of}\:\bigtriangleup{ABC} \\ $$$${at}\:{P},\:{Q},\:{R},\:{and}\:{S}\:{and}\:{reaches} \\ $$$${back}\:{to}\:{A}\:{thereupon},\:{find}\:\boldsymbol{\theta}\:{in} \\ $$$${terms}\:{of}\:\angle{A}=\alpha\:,\:\angle{B}=\beta\:,\:\angle{C}=\gamma\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Jun/18
$${pls}\:{wait}\:{i}\:{am}\:{trying}\:{to}\:{solve}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Jun/18

Answered by MrW3 last updated on 14/Jun/18

Commented by ajfour last updated on 14/Jun/18
$${thanks}\:{Sir},\:{but}\:{some}\:{explanation} \\ $$$${please}\:\left(\:{supporting}\:{the}\:{diagram}\right). \\ $$
Commented by MrW3 last updated on 14/Jun/18

$${if}\:\theta=\alpha−\beta,\:{the}\:{light}\:{ray}\:{will}\:{come}\:{back}\:{to} \\ $$$${its}\:{original}\:{point}\:{A}\:{after}\:{reflections} \\ $$$${on}\:{the}\:{walls}. \\ $$
