Question Number 37079 by rahul 19 last updated on 08/Jun/18
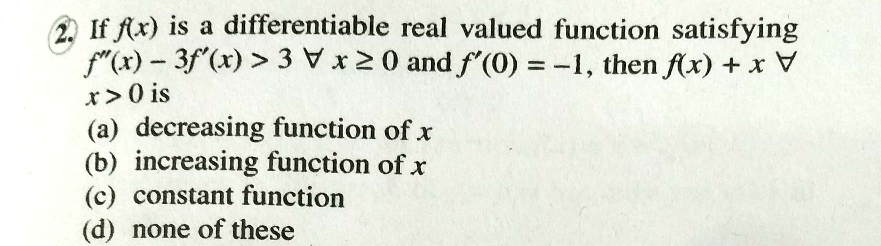
Answered by ajfour last updated on 09/Jun/18
![f ′′(x)−3f ′(x) > 3 ⇒ f ′′(0) > 0 for x > 0 f ′(x) > −1 ....(i) (d/dx)[ f(x)+x] = f ′(x)+1 ⇒ ((d[ f(x)+x])/dx) > 0 (using (i)) ⇒ increasing function of x. Option (b).](https://www.tinkutara.com/question/Q37082.png)
$${f}\:''\left({x}\right)−\mathrm{3}{f}\:'\left({x}\right)\:>\:\mathrm{3} \\ $$$$\Rightarrow\:\:\:{f}\:''\left(\mathrm{0}\right)\:>\:\mathrm{0} \\ $$$${for}\:{x}\:>\:\mathrm{0}\:\:{f}\:'\left({x}\right)\:>\:−\mathrm{1}\:\:\:\:\:\:\:….\left({i}\right) \\ $$$$\frac{{d}}{{dx}}\left[\:{f}\left({x}\right)+{x}\right]\:=\:{f}\:'\left({x}\right)+\mathrm{1}\: \\ $$$$\Rightarrow\:\:\frac{{d}\left[\:{f}\left({x}\right)+{x}\right]}{{dx}}\:>\:\mathrm{0}\:\:\:\:\:\:\:\left({using}\:\left({i}\right)\right) \\ $$$$\Rightarrow\:\:{increasing}\:{function}\:{of}\:{x}. \\ $$$$\:\:\:\:\:\:{Option}\:\left({b}\right). \\ $$
Commented by rahul 19 last updated on 08/Jun/18
Thank you sir ����
Commented by rahul 19 last updated on 08/Jun/18
typo in 1st line : it's 3f'(x) ��
