Question Number 37252 by Tinkutara last updated on 11/Jun/18
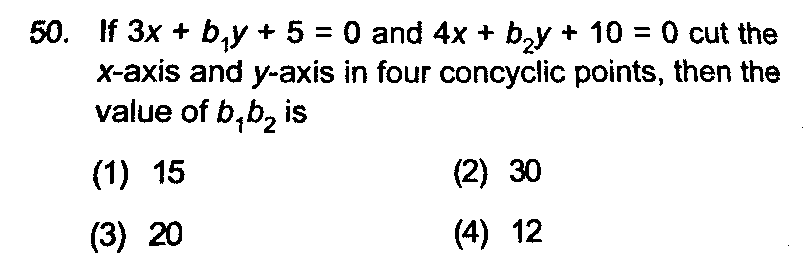
Commented by rahul 19 last updated on 11/Jun/18

$$\mathrm{3}×\mathrm{4}=\mathrm{b}_{\mathrm{1}} ×\mathrm{b}_{\mathrm{2}} \\ $$
Answered by ajfour last updated on 11/Jun/18
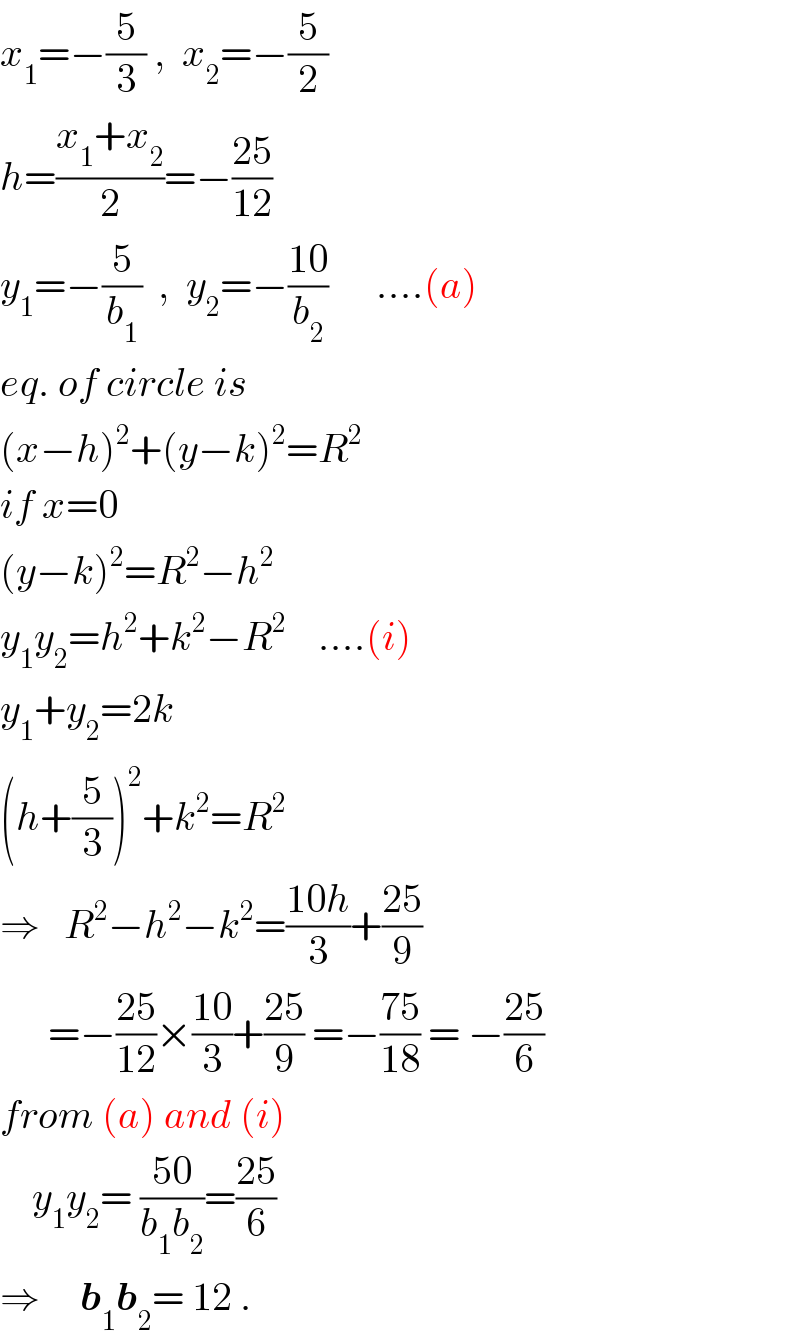
$${x}_{\mathrm{1}} =−\frac{\mathrm{5}}{\mathrm{3}}\:,\:\:{x}_{\mathrm{2}} =−\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${h}=\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} }{\mathrm{2}}=−\frac{\mathrm{25}}{\mathrm{12}} \\ $$$${y}_{\mathrm{1}} =−\frac{\mathrm{5}}{{b}_{\mathrm{1}} }\:\:,\:\:{y}_{\mathrm{2}} =−\frac{\mathrm{10}}{{b}_{\mathrm{2}} }\:\:\:\:\:\:….\left({a}\right) \\ $$$${eq}.\:{of}\:{circle}\:{is} \\ $$$$\left({x}−{h}\right)^{\mathrm{2}} +\left({y}−{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${if}\:{x}=\mathrm{0} \\ $$$$\left({y}−{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} −{h}^{\mathrm{2}} \\ $$$${y}_{\mathrm{1}} {y}_{\mathrm{2}} ={h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \:\:\:\:….\left({i}\right) \\ $$$${y}_{\mathrm{1}} +{y}_{\mathrm{2}} =\mathrm{2}{k} \\ $$$$\left({h}+\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{R}^{\mathrm{2}} −{h}^{\mathrm{2}} −{k}^{\mathrm{2}} =\frac{\mathrm{10}{h}}{\mathrm{3}}+\frac{\mathrm{25}}{\mathrm{9}} \\ $$$$\:\:\:\:\:\:=−\frac{\mathrm{25}}{\mathrm{12}}×\frac{\mathrm{10}}{\mathrm{3}}+\frac{\mathrm{25}}{\mathrm{9}}\:=−\frac{\mathrm{75}}{\mathrm{18}}\:=\:−\frac{\mathrm{25}}{\mathrm{6}} \\ $$$${from}\:\left({a}\right)\:{and}\:\left({i}\right) \\ $$$$\:\:\:\:{y}_{\mathrm{1}} {y}_{\mathrm{2}} =\:\frac{\mathrm{50}}{{b}_{\mathrm{1}} {b}_{\mathrm{2}} }=\frac{\mathrm{25}}{\mathrm{6}} \\ $$$$\Rightarrow\:\:\:\:\:\boldsymbol{{b}}_{\mathrm{1}} \boldsymbol{{b}}_{\mathrm{2}} =\:\mathrm{12}\:. \\ $$
Commented by Tinkutara last updated on 11/Jun/18
Thank you very much Sir! I got the answer. ��������
Commented by ajfour last updated on 11/Jun/18
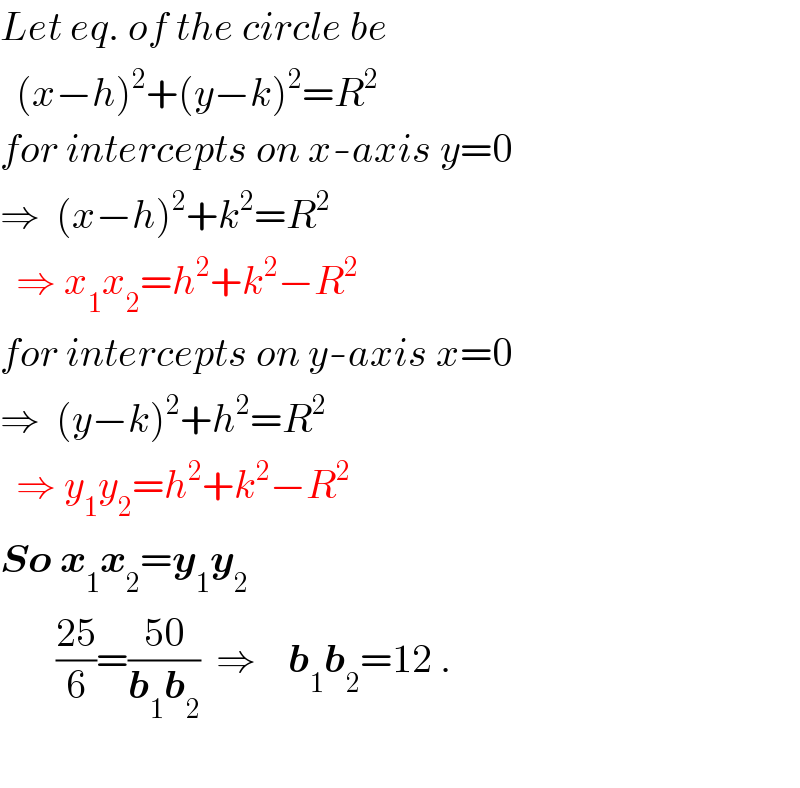
$${Let}\:{eq}.\:{of}\:{the}\:{circle}\:{be} \\ $$$$\:\:\left({x}−{h}\right)^{\mathrm{2}} +\left({y}−{k}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${for}\:{intercepts}\:{on}\:{x}-{axis}\:{y}=\mathrm{0} \\ $$$$\Rightarrow\:\:\left({x}−{h}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\:\:\Rightarrow\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} ={h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \\ $$$${for}\:{intercepts}\:{on}\:{y}-{axis}\:{x}=\mathrm{0} \\ $$$$\Rightarrow\:\:\left({y}−{k}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\:\:\Rightarrow\:{y}_{\mathrm{1}} {y}_{\mathrm{2}} ={h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{R}^{\mathrm{2}} \\ $$$$\boldsymbol{{So}}\:\boldsymbol{{x}}_{\mathrm{1}} \boldsymbol{{x}}_{\mathrm{2}} =\boldsymbol{{y}}_{\mathrm{1}} \boldsymbol{{y}}_{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{25}}{\mathrm{6}}=\frac{\mathrm{50}}{\boldsymbol{{b}}_{\mathrm{1}} \boldsymbol{{b}}_{\mathrm{2}} }\:\:\Rightarrow\:\:\:\:\boldsymbol{{b}}_{\mathrm{1}} \boldsymbol{{b}}_{\mathrm{2}} =\mathrm{12}\:. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 11/Jun/18
Thank you Sir.
