Menu Close

Question-37447

Tinku Tara 0 Comments
Pin




Question Number 37447 by ajfour last updated on 13/Jun/18
Commented by ajfour last updated on 13/Jun/18
Find the maximum elliptic area (in the shown orientation) cicumscribed by the isosceles triangle.
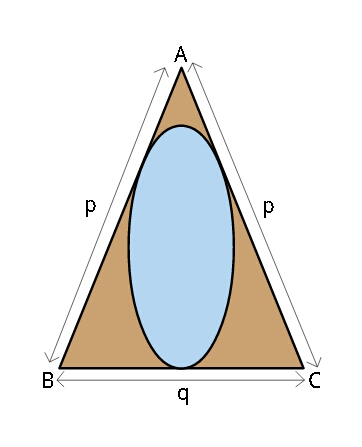
$${Find}\:{the}\:{maximum}\:{elliptic}\:{area} \\ $$$$\left({in}\:{the}\:{shown}\:{orientation}\right)\: \\ $$$${cicumscribed}\:{by}\:{the}\:{isosceles} \\ $$$${triangle}. \\ $$
Commented by MrW3 last updated on 13/Jun/18
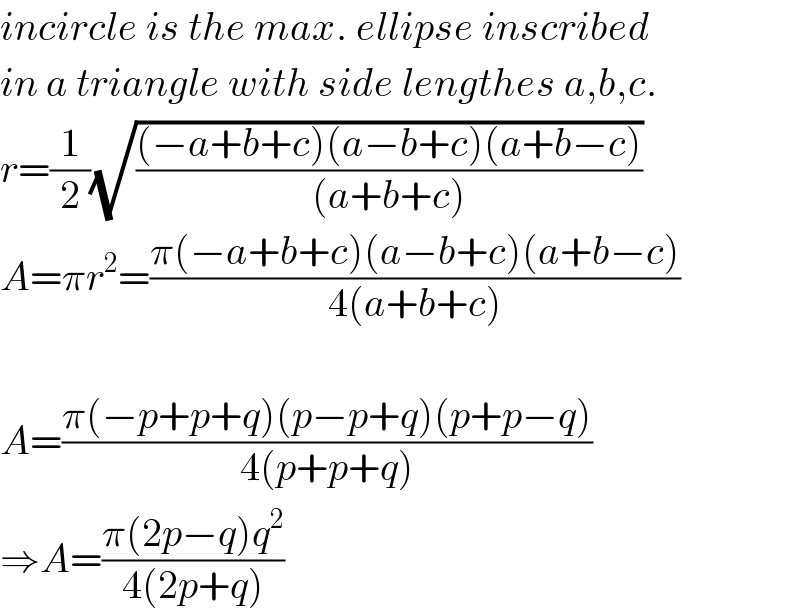
incircle is the max. ellipse inscribed in a triangle with side lengthes a,b,c. r=(1/2)(√(((−a+b+c)(a−b+c)(a+b−c))/((a+b+c)))) A=πr^2 =((π(−a+b+c)(a−b+c)(a+b−c))/(4(a+b+c))) A=((π(−p+p+q)(p−p+q)(p+p−q))/(4(p+p+q))) ⇒A=((π(2p−q)q^2 )/(4(2p+q)))
$${incircle}\:{is}\:{the}\:{max}.\:{ellipse}\:{inscribed} \\ $$$${in}\:{a}\:{triangle}\:{with}\:{side}\:{lengthes}\:{a},{b},{c}. \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}{\left({a}+{b}+{c}\right)}} \\ $$$${A}=\pi{r}^{\mathrm{2}} =\frac{\pi\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}{\mathrm{4}\left({a}+{b}+{c}\right)} \\ $$$$ \\ $$$${A}=\frac{\pi\left(−{p}+{p}+{q}\right)\left({p}−{p}+{q}\right)\left({p}+{p}−{q}\right)}{\mathrm{4}\left({p}+{p}+{q}\right)} \\ $$$$\Rightarrow{A}=\frac{\pi\left(\mathrm{2}{p}−{q}\right){q}^{\mathrm{2}} }{\mathrm{4}\left(\mathrm{2}{p}+{q}\right)} \\ $$
Commented by ajfour last updated on 13/Jun/18
Thank you Sir, but my solution fetches some other conclusion.
$${Thank}\:{you}\:{Sir},\:{but}\:{my}\:{solution} \\ $$$${fetches}\:{some}\:{other}\:{conclusion}. \\ $$
Commented by MJS last updated on 13/Jun/18
incircle is not the greatest ellipse inside a triangle and circumcircle is not the smallest ellipse surrounding it. see my answer below
$$\mathrm{incircle}\:\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{ellipse}\:\mathrm{inside}\:\mathrm{a} \\ $$$$\mathrm{triangle}\:\mathrm{and}\:\mathrm{circumcircle}\:\mathrm{is}\:\mathrm{not}\:\mathrm{the}\:\mathrm{smallest} \\ $$$$\mathrm{ellipse}\:\mathrm{surrounding}\:\mathrm{it}.\:\mathrm{see}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{below} \\ $$
Commented by MrW3 last updated on 13/Jun/18
Thanks for the information!
$${Thanks}\:{for}\:{the}\:{information}! \\ $$
Answered by ajfour last updated on 13/Jun/18
let altitude of triangle be h. Also let BC be x axis with mid point of BC as origin, the vertical as y axis. Since AC is tangent to ellipse, h−b=(√(a^2 m^2 +b^2 )) where m=(h/(q/2)) ⇒ a^2 =((h^2 −2bh)/m^2 ) ...(i) A_(ellipse) ^2 =π^2 a^2 b^2 let b=x ,then using (i) A_(ellipse) ^2 =π^2 (((h^2 −2hx)/m^2 ))x^2 (dA_(ellipse) ^2 /dx) = ((π^2 h)/m^2 )(hx^2 −2x^3 ) for max. area we have 2hx=6x^2 ⇒ b=x= (h/3) and using (i) a^2 =[h^2 −2((h/3))h]/m^2 a= (h/(m(√3))) ⇒ unless m=(√3) , max. area ellipse inscribed in triangle is not a circle. A_(ellipse, max) =𝛑((h/(m(√3))))((h/3)) and with m=(h/(q/2)) A_(ellipse , max) =((𝛑hq)/(6(√3))) = ((𝛑q(√(p^2 −(q^2 /4))))/(6(√3))) .
$${let}\:{altitude}\:{of}\:{triangle}\:{be}\:\boldsymbol{{h}}. \\ $$$${Also}\:{let}\:{BC}\:{be}\:{x}\:{axis}\:{with}\:{mid} \\ $$$${point}\:{of}\:{BC}\:{as}\:{origin},\:{the} \\ $$$${vertical}\:{as}\:{y}\:{axis}. \\ $$$${Since}\:{AC}\:{is}\:{tangent}\:{to}\:{ellipse}, \\ $$$$\:\:\:\:{h}−{b}=\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} }\: \\ $$$${where}\:{m}=\frac{{h}}{{q}/\mathrm{2}} \\ $$$$\:\:\Rightarrow\:\:{a}^{\mathrm{2}} =\frac{{h}^{\mathrm{2}} −\mathrm{2}{bh}}{{m}^{\mathrm{2}} }\:\:\:…\left({i}\right) \\ $$$${A}_{{ellipse}} ^{\mathrm{2}} =\pi^{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\:\:\:\:\:{let}\:\:{b}={x}\:,{then}\:{using}\:\left({i}\right) \\ $$$${A}_{{ellipse}} ^{\mathrm{2}} =\pi^{\mathrm{2}} \left(\frac{{h}^{\mathrm{2}} −\mathrm{2}{hx}}{{m}^{\mathrm{2}} }\right){x}^{\mathrm{2}} \\ $$$$\frac{{dA}_{{ellipse}} ^{\mathrm{2}} }{{dx}}\:=\:\frac{\pi^{\mathrm{2}} {h}}{{m}^{\mathrm{2}} }\left({hx}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{3}} \right) \\ $$$${for}\:{max}.\:{area}\:{we}\:{have} \\ $$$$\:\:\:\:\:\mathrm{2}{hx}=\mathrm{6}{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\boldsymbol{{b}}=\boldsymbol{{x}}=\:\frac{\boldsymbol{{h}}}{\mathrm{3}}\:\:{and}\:{using}\:\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{a}}^{\mathrm{2}} =\left[\boldsymbol{{h}}^{\mathrm{2}} −\mathrm{2}\left(\frac{{h}}{\mathrm{3}}\right){h}\right]/{m}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{{a}}=\:\frac{\boldsymbol{{h}}}{\boldsymbol{{m}}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:{unless}\:{m}=\sqrt{\mathrm{3}}\:\:\:,\:{max}.\:{area} \\ $$$${ellipse}\:{inscribed}\:{in}\:{triangle}\:{is} \\ $$$${not}\:{a}\:{circle}. \\ $$$${A}_{{ellipse},\:{max}} =\boldsymbol{\pi}\left(\frac{\boldsymbol{{h}}}{\boldsymbol{{m}}\sqrt{\mathrm{3}}}\right)\left(\frac{\boldsymbol{{h}}}{\mathrm{3}}\right) \\ $$$${and}\:{with}\:{m}=\frac{{h}}{{q}/\mathrm{2}}\: \\ $$$${A}_{{ellipse}\:,\:{max}} =\frac{\boldsymbol{\pi{hq}}}{\mathrm{6}\sqrt{\mathrm{3}}}\:=\:\frac{\boldsymbol{\pi{q}}\sqrt{\boldsymbol{{p}}^{\mathrm{2}} −\frac{\boldsymbol{{q}}^{\mathrm{2}} }{\mathrm{4}}}}{\mathrm{6}\sqrt{\mathrm{3}}}\:. \\ $$$$ \\ $$
Commented by MrW3 last updated on 13/Jun/18
Nice working!
$${Nice}\:{working}! \\ $$
Answered by MJS last updated on 13/Jun/18
I once promised to give you some formulas for the ellipse−triangle−problem triangle abc smallest ellipse surrounding the triangle a=((√(a^2 +b^2 +c^2 +2(√(a^2 b^2 +a^2 c^2 +b^2 c^2 −δ^2 ))))/3) b=((√(a^2 +b^2 +c^2 −2(√(a^2 b^2 +a^2 c^2 +b^2 c^2 −δ^2 ))))/3) e=(√(a^2 −b^2 ))=((2(√(a^2 b^2 +a^2 c^2 +b^2 c^2 −δ^2 )))/3) area=abπ=δ((√3)/9) δ=(√((a+b+c)(a+b−c)(a+c−b)(b+c−a))) the greatest ellipse inside the same triangle a_2 =(a/2); b_2 =(b/2); e_2 =(e/2); area=((abπ)/4)=δ((√3)/(36)) the center of both ellipses is the barycenter of the triangle for an equilateral triangle these ellipses are the circumcircle and the incircle the area of the greatest inner ellipse of the triangle ppq is ((√3)/(36))q(√(4p^2 −q^2 ))
$$\mathrm{I}\:\mathrm{once}\:\mathrm{promised}\:\mathrm{to}\:\mathrm{give}\:\mathrm{you}\:\mathrm{some}\:\mathrm{formulas} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{ellipse}−\mathrm{triangle}−\mathrm{problem} \\ $$$$\mathrm{triangle}\:{abc} \\ $$$$\mathrm{smallest}\:\mathrm{ellipse}\:\mathrm{surrounding}\:\mathrm{the}\:\mathrm{triangle} \\ $$$$\mathfrak{a}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} −\delta^{\mathrm{2}} }}}{\mathrm{3}} \\ $$$$\mathfrak{b}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} −\delta^{\mathrm{2}} }}}{\mathrm{3}} \\ $$$$\mathfrak{e}=\sqrt{\mathfrak{a}^{\mathrm{2}} −\mathfrak{b}^{\mathrm{2}} }=\frac{\mathrm{2}\sqrt{{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} −\delta^{\mathrm{2}} }}{\mathrm{3}} \\ $$$$\mathrm{area}=\mathfrak{ab}\pi=\delta\frac{\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$$$\delta=\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)\left({b}+{c}−{a}\right)} \\ $$$$\mathrm{the}\:\mathrm{greatest}\:\mathrm{ellipse}\:\mathrm{inside}\:\mathrm{the}\:\mathrm{same}\:\mathrm{triangle} \\ $$$$\mathfrak{a}_{\mathrm{2}} =\frac{\mathfrak{a}}{\mathrm{2}};\:\mathfrak{b}_{\mathrm{2}} =\frac{\mathfrak{b}}{\mathrm{2}};\:\mathfrak{e}_{\mathrm{2}} =\frac{\mathfrak{e}}{\mathrm{2}};\:\mathrm{area}=\frac{\mathfrak{ab}\pi}{\mathrm{4}}=\delta\frac{\sqrt{\mathrm{3}}}{\mathrm{36}} \\ $$$$\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{both}\:\mathrm{ellipses}\:\mathrm{is}\:\mathrm{the}\:\mathrm{barycenter} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{triangle} \\ $$$$\mathrm{for}\:\mathrm{an}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{these}\:\mathrm{ellipses}\:\mathrm{are} \\ $$$$\mathrm{the}\:\mathrm{circumcircle}\:\mathrm{and}\:\mathrm{the}\:\mathrm{incircle} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{inner}\:\mathrm{ellipse}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{triangle}\:{ppq}\:\mathrm{is}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{36}}{q}\sqrt{\mathrm{4}{p}^{\mathrm{2}} −{q}^{\mathrm{2}} } \\ $$
Commented by MJS last updated on 13/Jun/18
put the triangle like this A= ((((a^2 −b^2 −3c^2 )/(6c))),((−(δ/(6c)))) ) B= ((((a^2 −b^2 +3c^2 )/(6c))),((−(δ/(6c)))) ) C= ((((−a^2 +b^2 )/(3c))),((δ/(3c))) ) the barycenter is ((0),(0) ) the center and radius of the incircle C_I = (((((a−b)(a+b−3c))/(6c))),((((2c−a−b)δ)/(6(a+b+c)c))) ) r_I =(δ/(2(a+b+c))) the center and radius of the circumcircle C_C = ((((a^2 −b^2 )/(6c))),(((((a^2 +b^2 −c^2 )c)/(2δ))−(δ/(6c)))) ) R_C =((abc)/δ) the equation of the smallest surrounding ellipse δ^2 x^2 +2(a^2 −b^2 )δxy+((a^2 −b^2 )^2 +3c^4 )y^2 −((c^2 δ^2 )/3)=0r the equation of the greatest inner ellipse 4δ^2 x^2 +8(a^2 −b^2 )δxy+4((a^2 −b^2 )^2 +3c^4 )y^2 −((c^2 δ^2 )/3)=0
$$\mathrm{put}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{like}\:\mathrm{this} \\ $$$${A}=\begin{pmatrix}{\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{6}{c}}}\\{−\frac{\delta}{\mathrm{6}{c}}}\end{pmatrix} \\ $$$${B}=\begin{pmatrix}{\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{6}{c}}}\\{−\frac{\delta}{\mathrm{6}{c}}}\end{pmatrix} \\ $$$${C}=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{3}{c}}}\\{\frac{\delta}{\mathrm{3}{c}}}\end{pmatrix} \\ $$$$\mathrm{the}\:\mathrm{barycenter}\:\mathrm{is}\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{the}\:\mathrm{center}\:\mathrm{and}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{incircle} \\ $$$${C}_{{I}} =\begin{pmatrix}{\frac{\left({a}−{b}\right)\left({a}+{b}−\mathrm{3}{c}\right)}{\mathrm{6}{c}}}\\{\frac{\left(\mathrm{2}{c}−{a}−{b}\right)\delta}{\mathrm{6}\left({a}+{b}+{c}\right){c}}}\end{pmatrix} \\ $$$${r}_{{I}} =\frac{\delta}{\mathrm{2}\left({a}+{b}+\mathrm{c}\right)} \\ $$$$\mathrm{the}\:\mathrm{center}\:\mathrm{and}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circumcircle} \\ $$$${C}_{{C}} =\begin{pmatrix}{\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{6}{c}}}\\{\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right){c}}{\mathrm{2}\delta}−\frac{\delta}{\mathrm{6}{c}}}\end{pmatrix} \\ $$$${R}_{{C}} =\frac{{abc}}{\delta} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{surrounding} \\ $$$$\mathrm{ellipse} \\ $$$$\delta^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\delta{xy}+\left(\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{4}} \right){y}^{\mathrm{2}} −\frac{{c}^{\mathrm{2}} \delta^{\mathrm{2}} }{\mathrm{3}}=\mathrm{0r} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{inner}\:\mathrm{ellipse} \\ $$$$\mathrm{4}\delta^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{8}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\delta{xy}+\mathrm{4}\left(\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{4}} \right){y}^{\mathrm{2}} −\frac{{c}^{\mathrm{2}} \delta^{\mathrm{2}} }{\mathrm{3}}=\mathrm{0} \\ $$
Commented by ajfour last updated on 13/Jun/18
Thank you very much Sir.
$${Thank}\:{you}\:{very}\:{much}\:{Sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *