Question Number 38006 by ajfour last updated on 20/Jun/18
Commented by ajfour last updated on 20/Jun/18
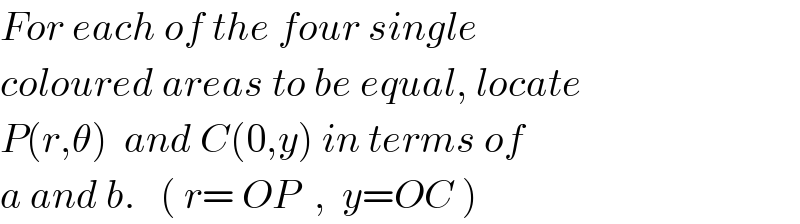
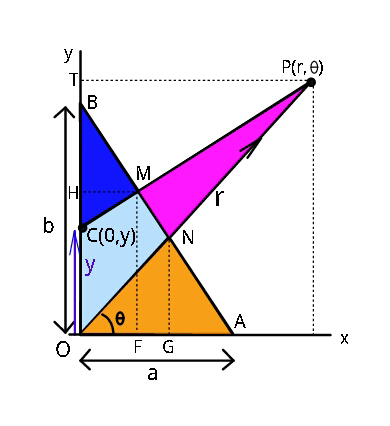
$${For}\:{each}\:{of}\:{the}\:{four}\:{single} \\ $$$${coloured}\:{areas}\:{to}\:{be}\:{equal},\:{locate} \\ $$$${P}\left({r},\theta\right)\:\:{and}\:{C}\left(\mathrm{0},{y}\right)\:{in}\:{terms}\:{of} \\ $$$${a}\:{and}\:{b}.\:\:\:\left(\:{r}=\:{OP}\:\:,\:\:{y}={OC}\:\right) \\ $$
Commented by Rio Mike last updated on 20/Jun/18

$$\:{Hi}\:{sir}\:{which}\:{app}\:{are}\:{you}\:{using} \\ $$$${to}\:{draw}\:{up}\:{the}\:{colour}\:{shapes} \\ $$
Commented by ajfour last updated on 20/Jun/18

$${Lekh}\:{diagram}. \\ $$
Commented by Rio Mike last updated on 21/Jun/18
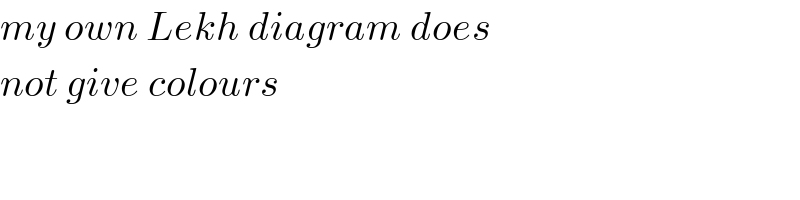
$${my}\:{own}\:{Lekh}\:{diagram}\:{does}\: \\ $$$${not}\:{give}\:{colours} \\ $$
Commented by ajfour last updated on 21/Jun/18

$${draw}\:{the}\:{shape},\:{touch}\:{the}\:{shape} \\ $$$${once},\:{touch}\:{top}\:{left}\:{corner}\:{option} \\ $$$${menu},\:{choose}\:\underset{\_\_\_} {{fill}}\:{at}\:{bottom}\:, \\ $$$${select}\:{color},\:{okay}. \\ $$
Answered by ajfour last updated on 21/Jun/18
![Area of △OAB = ((ab)/2) area of each single color regions =((ab)/6). area △ONA = (a/2)×NG = ((ab)/6) ⇒ NG =(b/3) OG+GA = a ⇒ NGcot θ+NG((a/b))=a (b/3)cot θ= a−(a/3) =((2a)/3) ⇒ tan θ = (b/(2a)) . area△OCP = (y/2)rcos θ = ((ab)/3) ⇒ rcos θ = ((2ab)/(3y)) .......(i) Let M≡(α,β) (β/(a−α))=(b/a) and ((β−y)/α)=((rsin θ−y)/(rcos θ)) ⇒ (((b/a)(a−α)−y)/α)=tan θ−(y/(rcos θ)) ((b(a−α)−ay)/(αa))=(b/(2a))−((3y^2 )/(2ab)) 2b(a−α)−2ay=α[b−((3y^2 )/b)] α = ((2ab(b−y))/(3(b^2 −y^2 ))) = ((2ab)/(3(b+y))) area △BCM = (α/2)(b−y)=((ab)/6) ⇒ ((ab(b−y))/(3(b+y)))=((ab)/6) ⇒ b+y = 2b−2y y = (b/3) . r= ((2ab)/(3ycos θ)) = (√(4a^2 +b^2 )) . rcos θ = 2a rsin θ = b .](https://www.tinkutara.com/question/Q38045.png)
$${Area}\:{of}\:\bigtriangleup{OAB}\:=\:\frac{{ab}}{\mathrm{2}} \\ $$$${area}\:{of}\:{each}\:{single}\:{color}\:{regions} \\ $$$$\:\:\:\:=\frac{{ab}}{\mathrm{6}}. \\ $$$${area}\:\bigtriangleup{ONA}\:=\:\frac{{a}}{\mathrm{2}}×{NG}\:=\:\frac{{ab}}{\mathrm{6}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:{NG}\:=\frac{{b}}{\mathrm{3}} \\ $$$$\:\:\:{OG}+{GA}\:=\:{a} \\ $$$$\Rightarrow\:\:\:\:{NG}\mathrm{cot}\:\theta+{NG}\left(\frac{{a}}{{b}}\right)={a} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{b}}{\mathrm{3}}\mathrm{cot}\:\theta=\:{a}−\frac{{a}}{\mathrm{3}}\:=\frac{\mathrm{2}{a}}{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:\:\:\:\mathrm{tan}\:\theta\:=\:\frac{{b}}{\mathrm{2}{a}}\:. \\ $$$${area}\bigtriangleup{OCP}\:=\:\frac{{y}}{\mathrm{2}}{r}\mathrm{cos}\:\theta\:=\:\frac{{ab}}{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:\:\:\:{r}\mathrm{cos}\:\theta\:=\:\frac{\mathrm{2}{ab}}{\mathrm{3}{y}}\:\:\:\:\:…….\left({i}\right) \\ $$$${Let}\:{M}\equiv\left(\alpha,\beta\right) \\ $$$$\:\:\:\:\frac{\beta}{{a}−\alpha}=\frac{{b}}{{a}}\:\:\:\:\:\:{and} \\ $$$$\:\:\:\:\:\:\:\frac{\beta−{y}}{\alpha}=\frac{{r}\mathrm{sin}\:\theta−{y}}{{r}\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\:\:\frac{\frac{{b}}{{a}}\left({a}−\alpha\right)−{y}}{\alpha}=\mathrm{tan}\:\theta−\frac{{y}}{{r}\mathrm{cos}\:\theta} \\ $$$$\:\:\:\:\:\frac{{b}\left({a}−\alpha\right)−{ay}}{\alpha{a}}=\frac{{b}}{\mathrm{2}{a}}−\frac{\mathrm{3}{y}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\:\:\:\mathrm{2}{b}\left({a}−\alpha\right)−\mathrm{2}{ay}=\alpha\left[{b}−\frac{\mathrm{3}{y}^{\mathrm{2}} }{{b}}\right] \\ $$$$\alpha\:=\:\frac{\mathrm{2}{ab}\left({b}−{y}\right)}{\mathrm{3}\left({b}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)}\:=\:\frac{\mathrm{2}{ab}}{\mathrm{3}\left({b}+{y}\right)} \\ $$$${area}\:\bigtriangleup{BCM}\:=\:\frac{\alpha}{\mathrm{2}}\left({b}−{y}\right)=\frac{{ab}}{\mathrm{6}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\frac{{ab}\left({b}−{y}\right)}{\mathrm{3}\left({b}+{y}\right)}=\frac{{ab}}{\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\:{b}+{y}\:=\:\mathrm{2}{b}−\mathrm{2}{y} \\ $$$$\:\:\:\:\:\:{y}\:=\:\frac{{b}}{\mathrm{3}}\:. \\ $$$$\:\:\:\:\:\:\:{r}=\:\frac{\mathrm{2}{ab}}{\mathrm{3}{y}\mathrm{cos}\:\theta}\:=\:\sqrt{\mathrm{4}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:. \\ $$$$\:\:\:\:\:{r}\mathrm{cos}\:\theta\:=\:\mathrm{2}{a}\: \\ $$$$\:\:\:\:\:{r}\mathrm{sin}\:\theta\:=\:{b}\:. \\ $$$$ \\ $$
