Question Number 38015 by ajfour last updated on 20/Jun/18
Commented by ajfour last updated on 20/Jun/18

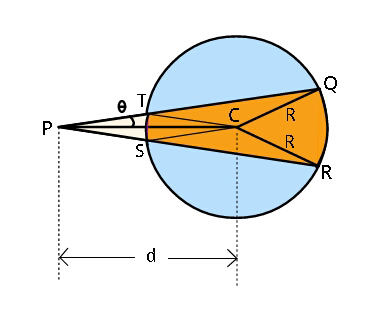
$${Find}\:\theta\:{in}\:{terms}\:{of}\:\boldsymbol{{d}},\:\boldsymbol{{R}}\:{if}\:{circle} \\ $$$${has}\:{all}\:{three}\:{coloured}\:{areas}\:{equal}. \\ $$
Commented by MrW3 last updated on 21/Jun/18
![let α=∠TCQ (1/3)×πR^2 =(R^2 /2)(α−sin α) ⇒sin α=α−((2π)/3) ⇒α=149.27° R cos ((α/2))=d sin θ ⇒θ=sin^(−1) [(R/d) cos (α/2)]=sin^(−1) (0.265(R/d))](https://www.tinkutara.com/question/Q38031.png)
$${let}\:\alpha=\angle{TCQ} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}×\pi{R}^{\mathrm{2}} =\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\alpha−\mathrm{sin}\:\alpha\right) \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\alpha−\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\alpha=\mathrm{149}.\mathrm{27}° \\ $$$$ \\ $$$${R}\:\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)={d}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\theta=\mathrm{sin}^{−\mathrm{1}} \left[\frac{{R}}{{d}}\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right]=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{265}\frac{{R}}{{d}}\right) \\ $$
Commented by ajfour last updated on 21/Jun/18
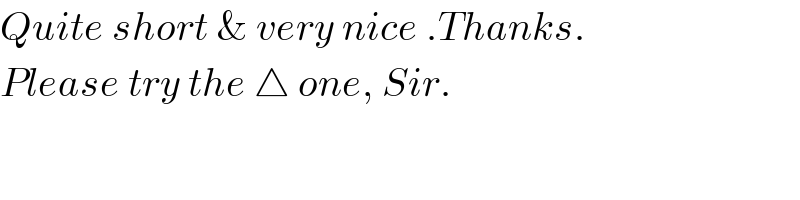
$${Quite}\:{short}\:\&\:{very}\:{nice}\:.{Thanks}. \\ $$$${Please}\:{try}\:{the}\:\bigtriangleup\:{one},\:{Sir}. \\ $$
Commented by ajfour last updated on 21/Jun/18
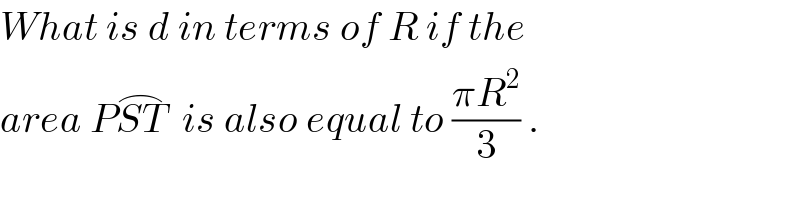
$${What}\:{is}\:{d}\:{in}\:{terms}\:{of}\:{R}\:{if}\:{the} \\ $$$${area}\:{P}\overset{\frown} {{ST}}\:\:{is}\:{also}\:{equal}\:{to}\:\frac{\pi{R}^{\mathrm{2}} }{\mathrm{3}}\:. \\ $$
Commented by MrW3 last updated on 21/Jun/18
![let β=∠QCR β=2[θ+(π/2)−(α/2)]=2θ+π−α A_(PQRP) =2×((πR^2 )/3) 2[(1/2)d^2 sin θcos θ+(1/2)R^2 sin (α/2)cos (α/2)]+((R^2 β)/2)=((2πR^2 )/3) ((d/R))^2 sin 2θ+sin α+β=((4π)/3) ((d/R))^2 sin 2θ+sin α+2θ+π−α=((4π)/3) since α−sin α=((2π)/3) ⇒((d/R))^2 sin 2θ+2θ+π−((2π)/3)=((4π)/3) ⇒((d/R))^2 sin 2θ+2θ=π since θ=sin^(−1) (((cos (α/2))/(d/R)))=sin^(−1) (((cos (α/2))/δ)) let δ=(d/R) sin 2θ=2sin θcos θ=2×((cos (α/2))/δ)×(√(1−(((cos (α/2))/δ))^2 )) ⇒δ^2 2×((cos (α/2))/δ)×(√(1−(((cos (α/2))/δ))^2 ))+2sin^(−1) (((cos (α/2))/δ))=π ⇒δ cos (α/2)×(√(1−(((cos (α/2))/δ))^2 ))+sin^(−1) (((cos (α/2))/δ))=(π/2) ⇒δ cos (α/2)×(√(1−(((cos (α/2))/δ))^2 ))=(π/2)−sin^(−1) (((cos (α/2))/δ)) ⇒cos^2 (α/2)(√(1−(((cos (α/2))/δ))^2 ))=((cos (α/2))/δ)((π/2)−sin^(−1) (((cos (α/2))/δ))) with α=149.27° ⇒δ=5.7612 ⇒d=5.7612R](https://www.tinkutara.com/question/Q38048.png)
$${let}\:\beta=\angle{QCR} \\ $$$$\beta=\mathrm{2}\left[\theta+\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}\right]=\mathrm{2}\theta+\pi−\alpha \\ $$$${A}_{{PQRP}} =\mathrm{2}×\frac{\pi{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{2}}{d}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}{R}^{\mathrm{2}} \mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}\right]+\frac{{R}^{\mathrm{2}} \beta}{\mathrm{2}}=\frac{\mathrm{2}\pi{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\left(\frac{{d}}{{R}}\right)^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta+\mathrm{sin}\:\alpha+\beta=\frac{\mathrm{4}\pi}{\mathrm{3}} \\ $$$$\left(\frac{{d}}{{R}}\right)^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta+\mathrm{sin}\:\alpha+\mathrm{2}\theta+\pi−\alpha=\frac{\mathrm{4}\pi}{\mathrm{3}} \\ $$$${since}\:\alpha−\mathrm{sin}\:\alpha=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\left(\frac{{d}}{{R}}\right)^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta+\mathrm{2}\theta+\pi−\frac{\mathrm{2}\pi}{\mathrm{3}}=\frac{\mathrm{4}\pi}{\mathrm{3}} \\ $$$$\Rightarrow\left(\frac{{d}}{{R}}\right)^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta+\mathrm{2}\theta=\pi \\ $$$${since}\:\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\frac{{d}}{{R}}}\right)=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right) \\ $$$${let}\:\delta=\frac{{d}}{{R}} \\ $$$$\mathrm{sin}\:\mathrm{2}\theta=\mathrm{2sin}\:\theta\mathrm{cos}\:\theta=\mathrm{2}×\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}×\sqrt{\mathrm{1}−\left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\delta^{\mathrm{2}} \mathrm{2}×\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}×\sqrt{\mathrm{1}−\left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right)^{\mathrm{2}} }+\mathrm{2sin}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right)=\pi \\ $$$$\Rightarrow\delta\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}×\sqrt{\mathrm{1}−\left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right)^{\mathrm{2}} }+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\delta\:\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}×\sqrt{\mathrm{1}−\left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right)^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right) \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\sqrt{\mathrm{1}−\left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right)^{\mathrm{2}} }=\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\left(\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{cos}\:\frac{\alpha}{\mathrm{2}}}{\delta}\right)\right) \\ $$$${with}\:\alpha=\mathrm{149}.\mathrm{27}° \\ $$$$\Rightarrow\delta=\mathrm{5}.\mathrm{7612} \\ $$$$\Rightarrow{d}=\mathrm{5}.\mathrm{7612}{R} \\ $$
Commented by ajfour last updated on 21/Jun/18
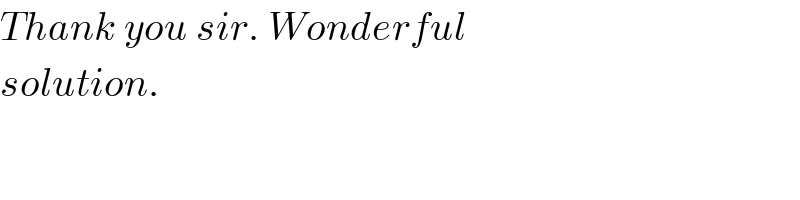
$${Thank}\:{you}\:{sir}.\:{Wonderful} \\ $$$${solution}. \\ $$
