Question Number 38247 by ajfour last updated on 23/Jun/18
Commented by ajfour last updated on 23/Jun/18
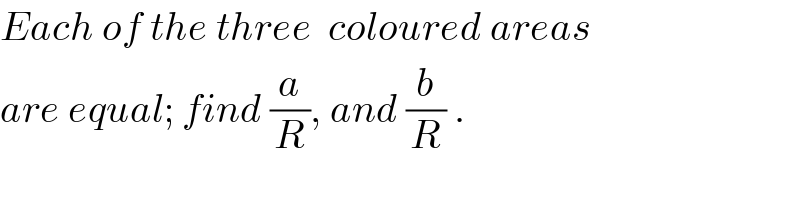
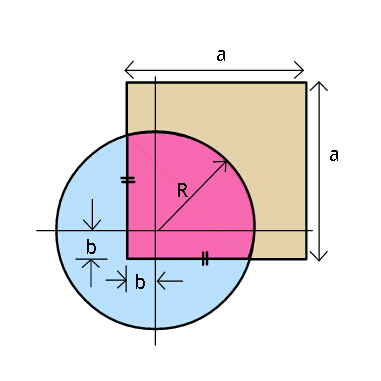
$${Each}\:{of}\:{the}\:{three}\:\:{coloured}\:{areas} \\ $$$${are}\:{equal};\:{find}\:\frac{{a}}{{R}},\:{and}\:\frac{{b}}{{R}}\:. \\ $$
Commented by behi83417@gmail.com last updated on 23/Jun/18

$${sir}\:{Ajfour}!\:{please}\:{check}\:{my}\:{comment} \\ $$$${on}\:{Q}#\mathrm{38151}. \\ $$
Answered by behi83417@gmail.com last updated on 25/Jun/18
![eq. of circle: x^2 +y^2 =R^2 z^2 =R^2 −b^2 ⇒z=(√(R^2 −b^2 )) S_z =∫_(−b) ^0 [((√(R^2 −x^2 ))−((√(R^2 −b^2 )))]dx= =[−(x/2)(√(R^2 −x^2 ))+(R^2 /2)sin^(−1) (x/R)−x(√(R^2 −b^2 ))]_(−b) ^0 = =[(R^2 /2)sin^(−1) (b/R)−((3b)/2)(√(R^2 −b^2 ))] S_(pink) =((πR^2 )/4)+b^2 +2b(√(R^2 −b^2 ))+2S_z S_(blue) =((3πR^2 )/4)−b^2 −2b(√(R^2 −b^2 ))−2S_z ⇒((πR^2 )/2)−2b^2 −4b(√(R^2 −b^2 ))=4S_z ((πR^2 )/2)−2b^2 −4b(√(R^2 −b^2 ))=2R^2 sin^(−1) (b/R)−6b(√(R^2 −b^2 )) ((πR^2 )/2)−2b^2 +2b(√(R^2 −b^2 ))−2R^2 sin^(−1) (b/R)=0 π−4(b^2 /R^2 )+4(b/R)(√(1−(b^2 /R^2 )))−4sin^(−1) (b/R)=0 ⇒^((b/R)=m) m^2 −m(√(1−m^2 ))+sin^(−1) m−(π/4)=0 ⇒m=(b/R)=0.71](https://www.tinkutara.com/question/Q38388.png)
$${eq}.\:{of}\:{circle}:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} ={R}^{\mathrm{2}} −{b}^{\mathrm{2}} \Rightarrow{z}=\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${S}_{{z}} =\underset{−{b}} {\overset{\mathrm{0}} {\int}}\left[\left(\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }−\left(\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)\right]{dx}=\right. \\ $$$$=\left[−\frac{{x}}{\mathrm{2}}\sqrt{{R}^{\mathrm{2}} −{x}^{\mathrm{2}} }+\frac{{R}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{{x}}{{R}}−{x}\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }\underset{−{b}} {\overset{\mathrm{0}} {\right]}}= \\ $$$$=\left[\frac{{R}^{\mathrm{2}} }{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{{b}}{{R}}−\frac{\mathrm{3}{b}}{\mathrm{2}}\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right] \\ $$$${S}_{{pink}} =\frac{\pi{R}^{\mathrm{2}} }{\mathrm{4}}+{b}^{\mathrm{2}} +\mathrm{2}{b}\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }+\mathrm{2}{S}_{{z}} \\ $$$${S}_{{blue}} =\frac{\mathrm{3}\pi{R}^{\mathrm{2}} }{\mathrm{4}}−{b}^{\mathrm{2}} −\mathrm{2}{b}\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }−\mathrm{2}{S}_{{z}} \\ $$$$\Rightarrow\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{b}^{\mathrm{2}} −\mathrm{4}{b}\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\mathrm{4}{S}_{{z}} \\ $$$$\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{b}^{\mathrm{2}} −\mathrm{4}{b}\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\mathrm{2}{R}^{\mathrm{2}} {sin}^{−\mathrm{1}} \frac{{b}}{{R}}−\mathrm{6}{b}\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{b}\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }−\mathrm{2}{R}^{\mathrm{2}} {sin}^{−\mathrm{1}} \frac{{b}}{{R}}=\mathrm{0} \\ $$$$\pi−\mathrm{4}\frac{{b}^{\mathrm{2}} }{{R}^{\mathrm{2}} }+\mathrm{4}\frac{{b}}{{R}}\sqrt{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{R}^{\mathrm{2}} }}−\mathrm{4}{sin}^{−\mathrm{1}} \frac{{b}}{{R}}=\mathrm{0} \\ $$$$\overset{\frac{{b}}{{R}}={m}} {\Rightarrow}\boldsymbol{{m}}^{\mathrm{2}} −\boldsymbol{{m}}\sqrt{\mathrm{1}−\boldsymbol{{m}}^{\mathrm{2}} }+\boldsymbol{{sin}}^{−\mathrm{1}} \boldsymbol{{m}}−\frac{\pi}{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{m}}=\frac{\boldsymbol{{b}}}{\boldsymbol{{R}}}=\mathrm{0}.\mathrm{71}\: \\ $$
Commented by behi83417@gmail.com last updated on 25/Jun/18
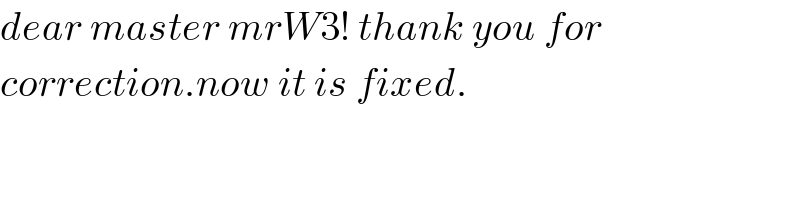
$${dear}\:{master}\:{mrW}\mathrm{3}!\:{thank}\:{you}\:{for} \\ $$$${correction}.{now}\:{it}\:{is}\:{fixed}. \\ $$
Commented by ajfour last updated on 25/Jun/18
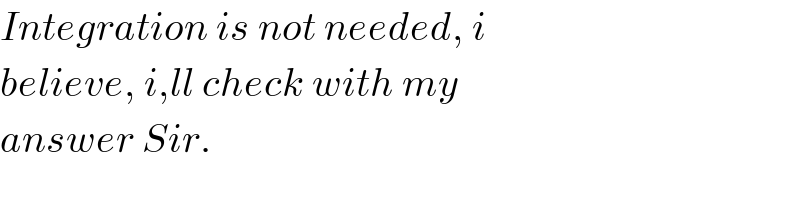
$${Integration}\:{is}\:{not}\:{needed},\:{i} \\ $$$${believe},\:{i},{ll}\:{check}\:{with}\:{my} \\ $$$${answer}\:{Sir}. \\ $$
Commented by MrW3 last updated on 25/Jun/18
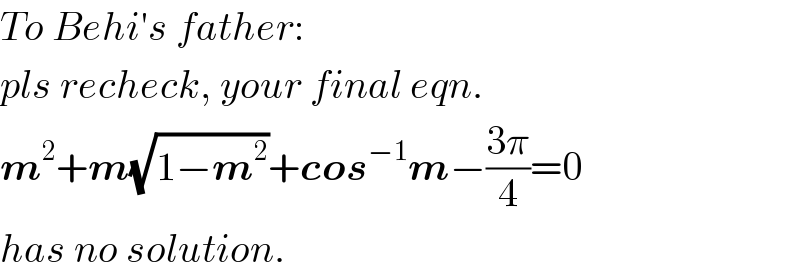
$${To}\:{Behi}'{s}\:{father}: \\ $$$${pls}\:{recheck},\:{your}\:{final}\:{eqn}.\: \\ $$$$\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{m}}\sqrt{\mathrm{1}−\boldsymbol{{m}}^{\mathrm{2}} }+\boldsymbol{{cos}}^{−\mathrm{1}} \boldsymbol{{m}}−\frac{\mathrm{3}\pi}{\mathrm{4}}=\mathrm{0} \\ $$$${has}\:{no}\:{solution}. \\ $$
Commented by MrW3 last updated on 25/Jun/18
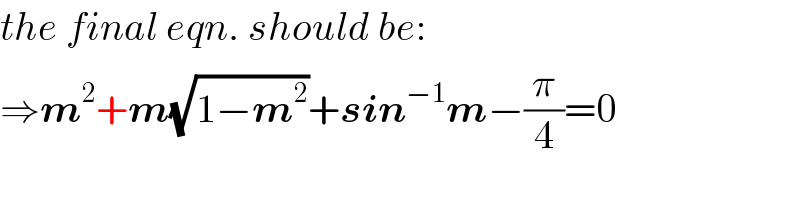
$${the}\:{final}\:{eqn}.\:{should}\:{be}: \\ $$$$\Rightarrow\boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{m}}\sqrt{\mathrm{1}−\boldsymbol{{m}}^{\mathrm{2}} }+\boldsymbol{{sin}}^{−\mathrm{1}} \boldsymbol{{m}}−\frac{\pi}{\mathrm{4}}=\mathrm{0} \\ $$
Answered by MrW3 last updated on 25/Jun/18
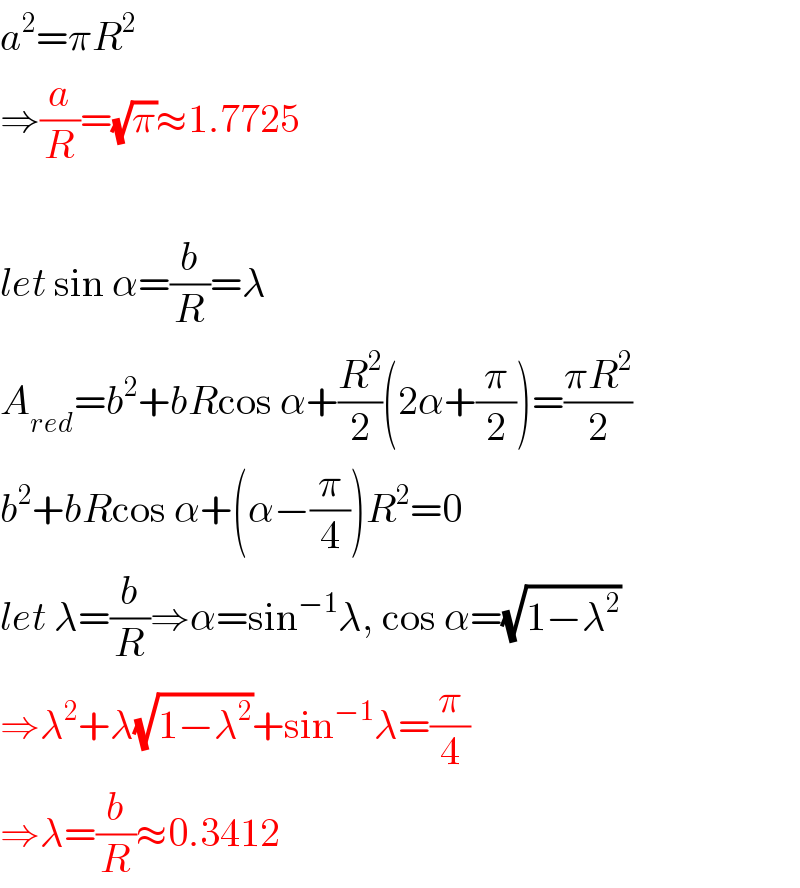
$${a}^{\mathrm{2}} =\pi{R}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{a}}{{R}}=\sqrt{\pi}\approx\mathrm{1}.\mathrm{7725} \\ $$$$ \\ $$$${let}\:\mathrm{sin}\:\alpha=\frac{{b}}{{R}}=\lambda \\ $$$${A}_{{red}} ={b}^{\mathrm{2}} +{bR}\mathrm{cos}\:\alpha+\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\alpha+\frac{\pi}{\mathrm{2}}\right)=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} +{bR}\mathrm{cos}\:\alpha+\left(\alpha−\frac{\pi}{\mathrm{4}}\right){R}^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:\lambda=\frac{{b}}{{R}}\Rightarrow\alpha=\mathrm{sin}^{−\mathrm{1}} \lambda,\:\mathrm{cos}\:\alpha=\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$\Rightarrow\lambda^{\mathrm{2}} +\lambda\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }+\mathrm{sin}^{−\mathrm{1}} \lambda=\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\lambda=\frac{{b}}{{R}}\approx\mathrm{0}.\mathrm{3412} \\ $$
Commented by behi83417@gmail.com last updated on 25/Jun/18

$${dear}\:{Ajfour}!\:{please}\:{recheck}\:{my}\:{new} \\ $$$${edition}\:{for}\:{your}\:{question}.{thanks}. \\ $$
Commented by ajfour last updated on 25/Jun/18
$${Thank}\:{you}\:{both},\:{Sirs}. \\ $$
