Question Number 38289 by Tinkutara last updated on 23/Jun/18

Answered by tanmay.chaudhury50@gmail.com last updated on 23/Jun/18
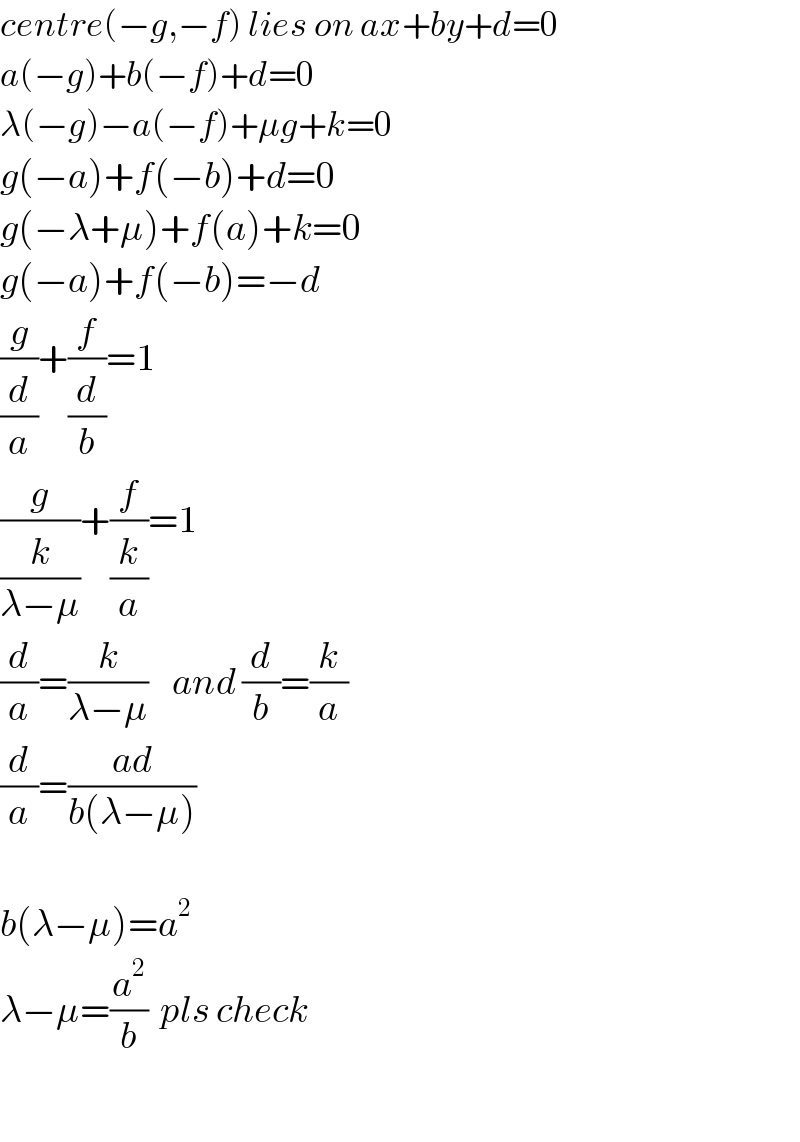
$${centre}\left(−{g},−{f}\right)\:{lies}\:{on}\:{ax}+{by}+{d}=\mathrm{0} \\ $$$${a}\left(−{g}\right)+{b}\left(−{f}\right)+{d}=\mathrm{0}\: \\ $$$$\lambda\left(−{g}\right)−{a}\left(−{f}\right)+\mu{g}+{k}=\mathrm{0} \\ $$$${g}\left(−{a}\right)+{f}\left(−{b}\right)+{d}=\mathrm{0} \\ $$$${g}\left(−\lambda+\mu\right)+{f}\left({a}\right)+{k}=\mathrm{0} \\ $$$${g}\left(−{a}\right)+{f}\left(−{b}\right)=−{d} \\ $$$$\frac{{g}}{\frac{{d}}{{a}}}+\frac{{f}}{\frac{{d}}{{b}}}=\mathrm{1} \\ $$$$\frac{{g}}{\frac{{k}}{\lambda−\mu}}+\frac{{f}}{\frac{{k}}{{a}}}=\mathrm{1} \\ $$$$\frac{{d}}{{a}}=\frac{{k}}{\lambda−\mu}\:\:\:\:{and}\:\frac{{d}}{{b}}=\frac{{k}}{{a}} \\ $$$$\frac{{d}}{{a}}=\frac{{ad}}{{b}\left(\lambda−\mu\right)} \\ $$$$ \\ $$$${b}\left(\lambda−\mu\right)={a}^{\mathrm{2}} \\ $$$$\lambda−\mu=\frac{{a}^{\mathrm{2}} }{{b}}\:\:{pls}\:{check} \\ $$$$ \\ $$
Commented by Tinkutara last updated on 23/Jun/18
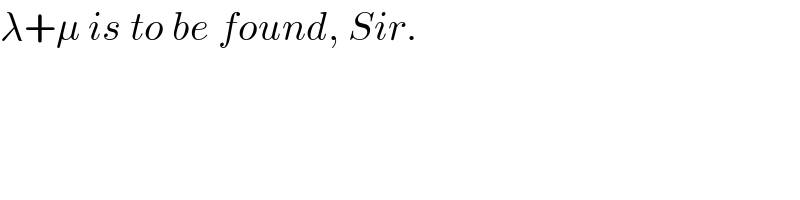
$$\lambda+\mu\:{is}\:{to}\:{be}\:{found},\:{Sir}. \\ $$
